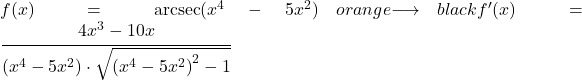مشتق قوسي

في هذه الصفحة سترى ما هو مشتق القاطع القوسي (الصيغة). ستجد تمارين محلولة لمشتقات قاطع الدالة.

صيغة مشتقة قوسية

مشتق القاطع القوسي لـ x هو واحد على منتج x في جذر x تربيع ناقص 1.

f(x)=\text{arcsec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x\cdot \sqrt{x^2-1}}

ومن ثم، فإن مشتقة القاطع القوسي لدالة تساوي حاصل قسمة مشتقة تلك الدالة على الدالة في جذر تلك الدالة تربيع ناقص واحد.

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

من الواضح أن الصيغة الثانية تشبه الصيغة الأولى، والفرق الوحيد بين الاثنين هو أن قاعدة السلسلة يتم تطبيقها في الصيغة الثانية.

مشتق من القاطع القوسي

على الرغم من أن الأمر قد يبدو غريبًا لأنها دوال عكسية، إلا أن مشتقة القاطع القوسي لا علاقة لها بمشتقة القاطع. يمكنك رؤية صيغة مشتق القاطع بالضغط هنا:

➤ انظر: مشتقة القاطع

أمثلة على مشتق قوسي

مثال 1

في هذا المثال، سنرى ما مقدار مشتقة قاطع القوس للدالة الخطية 7x.

f(x)=\text{arcsec}(7x)

للعثور على مشتقة القاطع القوسي، يجب عليك تطبيق الصيغة المقابلة لها، وهي كما يلي:

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

مشتقة الدالة 7x هي 7، لذا فإن مشتقة القاطع القوسي للدالة 7x هي:

f(x)=\text{arcsec}(7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{7}{7x\cdot \sqrt{(7x)^2-1}}=\cfrac{1}{x\cdot \sqrt{49x^2-1}}

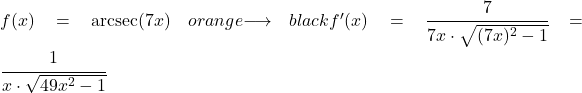
مثال 2

في هذا المثال الثاني، سنشتق القاطع القوسي لدالة محتملة.

f(x)=\text{arcsec}(x^4-5x^2)

نظرًا لوجود مصطلح آخر غير x في وسيطة الدالة القوسية، نحتاج إلى تطبيق قاعدة المشتقة القوسية مع قاعدة السلسلة لاشتقاق الدالة بأكملها.

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

لذلك، نكتب في البسط مشتقة وسيطة الدالة، وفي المقام نعيد كتابة دالة الجهد ونضربها في الجذر التربيعي لدالة وسيطة الدالة مرفوعة للأس 2 ناقص 1:

f(x)=\text{arcsec}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{(x^4-5x^2)\cdot \sqrt{\left(x^4-5x^2\right)^2-1}}

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top