▷ كيفية إزالة (أو استخراج) العامل المشترك ✅ (تمارين محلولة)

نشرح في هذه الصفحة كيفية أخذ (أو استخراج) العامل المشترك لكثيرة الحدود. ستجد هنا الأنواع المختلفة للعامل المشترك وستكون قادرًا على رؤية عدة أمثلة لكيفية تحقيق ذلك. بالإضافة إلى ذلك، يمكنك التدرب مع التمارين التي تم حلها خطوة بخطوة.

ما هو العامل المشترك؟

في الرياضيات، العامل المشترك هو عامل موجود في جميع حدود كثيرة الحدود، أي أن العامل المشترك يتكون من رقم أو حرف يضرب كل حد من كثيرات الحدود.

على سبيل المثال، سوف نحدد ما هو العامل المشترك لكثيرة الحدود التالية:

$4x+4y$

في الرقم 4 يتكرر في جميع حدود كثيرة الحدود:

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

وبالتالي فإن العامل المشترك لكثيرة الحدود هذا يساوي 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

كيفية الحصول على (أو استخراج) العامل المشترك

بمجرد أن نعرف معنى العامل المشترك، دعونا نرى كيفية الحصول على العامل المشترك من كثيرة الحدود.

عندما يكون هناك عامل مشترك بين حدين أو أكثر من كثيرة الحدود، يمكن أخذ العامل المشترك (أو استخلاصه) لتحويل عمليات الإضافة أو الطرح لكثيرة الحدود إلى ضرب.

قد يبدو هذا صعبًا بعض الشيء في الكتابة، لذلك دعونا نرى كيفية استخراج العامل المشترك من كثيرة الحدود بمثال:

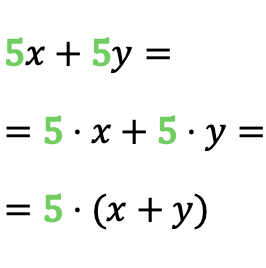
استخراج أو إزالة العامل المشترك من كثيرة الحدود

كما ترون في المثال، الرقم 5 يتكرر في أحادية الحد 5x وفي أحادية الحد 5y، وبالتالي فإن العامل المشترك لكثيرة الحدود هو 5. لذلك بمجرد تحديد العامل المشترك، يمكننا تحويل مجموع أحاديات الحد في منتج.

ولا تنس وضع القوسين عند استخراج العامل المشترك، لأن العامل المشترك يجب أن يضاعف جميع الإضافات.

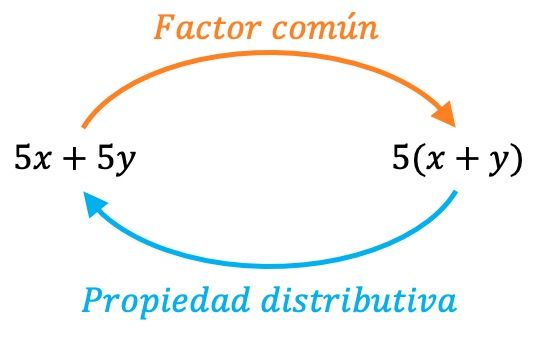
إزالة العامل المشترك هي العملية العكسية لخاصية التوزيع ، أي أننا في الواقع نطبق خاصية التوزيع في الاتجاه المعاكس. لذلك، يمكننا دائمًا التحقق من أننا استخرجنا العامل المشترك بشكل صحيح عن طريق إجراء العملية العكسية:

إذا حصلنا، بتطبيق خاصية التوزيع، على كثيرة الحدود نفسها من البداية، فهذا يعني أننا حصلنا على العامل المشترك بشكل صحيح.
ومن ناحية أخرى، عندما تكون نتيجة استخدام خاصية التوزيع كثيرة حدود أخرى تختلف عن كثيرة الحدود الأصلية، فهذا يعني أننا ارتكبنا خطأ في عملية استخراج العامل المشترك.

أمثلة على أخذ (أو استخلاص) العامل المشترك

نترككم مع المزيد من الأمثلة للانتهاء من فهم مفهوم العامل المشترك:

مثال 1

كما ترى في هذا المثال، يمكن استخراج العامل المشترك من أكثر من حدين في نفس الوقت:

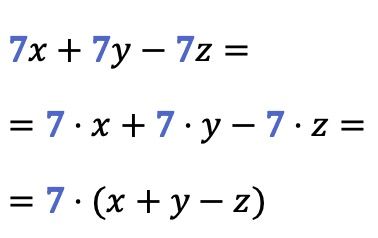
مثال 2

يمكنك أيضًا استخراج عامل مشترك من المتغيرات (أو الحروف):

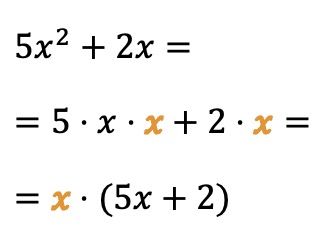
استخراج العامل المشترك في التعابير الجبرية

في هذه الحالة، يقوم الحرف x بضرب حدي كثيرة الحدود، لذا يمكننا تبسيط التعبير الجبري بأخذ المتغير x كعامل مشترك.

مثال 3

في هذا المثال، الحد الأول به المتغير x مرفوع للأس 3 وفي الحد الثاني x مرفوع للأس 2، لذا فإن كلا الحدين يحتوي على علامتي x. وبالتالي فإن العامل المشترك ليس مجرد x، بل x ² :

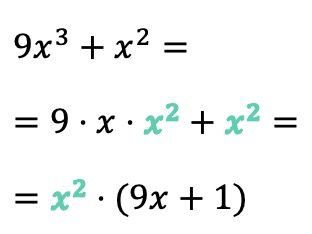
من ناحية أخرى، لاحظ أنه إذا كان العامل المشترك لكثيرة الحدود يتطابق تمامًا مع الحد، فعندما نستخرج العامل المشترك، يجب أن نضع 1 في مكانه . وإلا فإننا إذا لم نضع شيئا في مكانه، فلن نحصل على تعبير مكافئ.

مثال 4

في بعض الأحيان لا يكون العامل المشترك واضحًا جدًا ولا يكون مرئيًا بشكل مباشر، بل هو مقسوم على معاملات أحاديات الحد. على سبيل المثال، العامل المشترك في المثال التالي هو 3، حيث أن التحليل العاملي للعددين 6 و9 يحتوي على 3:

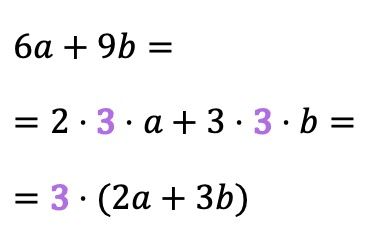
ويسمى هذا النوع من العامل المشترك في بعض كتب الجبر بالعامل المشترك الأقصى ، حيث أن العامل المشترك هو في نفس الوقت العامل المشترك الأكبر (GCD) لمعاملات الحدود كثيرة الحدود.

إذا وصلت إلى هذا الحد، فهذا يعني أنك ربما تعرف بالفعل كيفية إيجاد العامل المشترك لكثيرة الحدود، وهو الكمال. ومع ذلك، ألم تتساءل ما هو العامل المشترك؟ حسنًا، أحد تطبيقات العامل المشترك هو أنه يتم استخدامه لتحليل كثيرات الحدود. إذا كنت لا تزال لا تعرف ما هو، في هذا الرابط يمكنك أن ترى ما هو تحليل كثيرات الحدود وسبب أهمية العامل المشترك لإجراء هذه العملية متعددة الحدود.

العامل المشترك للكسور

العامل المشترك مفيد جدًا أيضًا لتبسيط الحدود إلى كسور ذات كثيرات حدود في البسط والمقام.

لمعرفة كيفية القيام بذلك، دعونا نبسط الكسر التالي كمثال:

$\cfrac{2x^2+4}{14x+8y}$

أول ما علينا فعله هو إيجاد العامل المشترك بين بسط كثير الحدود ومقام كثير الحدود. في هذه الحالة، العامل المشترك بين كثيرتي الحدود هو 2:

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

الآن دعونا نستخرج العامل المشترك بين كثيرتي الحدود:

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

وبمجرد حصولنا على عامل مشترك لكلا كثيرتي الحدود، نحتاج إلى إزالة العوامل المتكررة في البسط والمقام :

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

في الختام، الكسر المبسط هو:

$\cfrac{x^2+2}{7x+4y}$

العامل المشترك حسب التجميع

إحدى طرق تقليل حدود كثيرة الحدود هي استخدام طريقة العامل المشترك عن طريق تجميع الحدود ، والتي تسمى أيضًا استخراج العامل المشترك المزدوج. كما يوحي اسمها، يتكون هذا الإجراء من تبسيط تعبير كثيرة الحدود عن طريق تجميع حدودها مرتين.

هذه الطريقة معقدة بعض الشيء، لذلك دعونا نرى كيف يتم تطبيقها خطوة بخطوة مع كثير الحدود التالي:

$x^2+2x+5x+10$

نحتاج أولاً إلى تحديد عاملين مشتركين مختلفين، لذلك نقوم بفصل كثير الحدود إلى قسمين:

$(x^2+2x)+(5x+10)$

في هذه الحالة، العنصران x ² و2x لديهما الحرف x كعامل مشترك، والمصطلحان 5x و10 لهما 5 كعامل مشترك (نظرًا لأن 10 من مضاعفات الرقم 5). لذلك لدينا هذين العاملين المشتركين:

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

وأخيرًا، بما أن ناتجي كثيرات الحدود المتبقيين لهما العامل (x+2)، فيمكننا تبسيط كثيرة الحدود على النحو التالي:

$(x+2)\cdot (x+5)$

كما ترون، هذه الطريقة ليست سهلة على الإطلاق. لذلك لا تتردد في طرح أي أسئلة لديك في التعليقات، وسوف نقوم بالرد عليها في أقرب وقت ممكن.

تمارين العوامل المشتركة تم حلها خطوة بخطوة

نترك لك العديد من التمارين التي تم حلها خطوة بخطوة حتى تتمكن من التدرب على استخراج العامل المشترك من كثيرة الحدود.

التمرين 1

استخرج العامل المشترك من كثيرات الحدود التالية:

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

انظر الحل

أ) جميع الحدود التي تشكل كثيرة الحدود الأولى لها 6، وبالتالي فإن العامل المشترك لكثيرة الحدود هو 6:

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

ب) في كثيرة الحدود الثانية، جميع عناصرها تحتوي على حرف واحد على الأقل x. هنا هو العامل المشترك لكثيرة الحدود:

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

ج) من الواضح أن أحادية الحد الأولى من كثيرة الحدود لها 2، ووحيدة الحد الثانية هي مضاعف 2. وبالتالي فإن العامل المشترك لكثيرة الحدود هو 2:

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

د) في كثير الحدود الأخير تكون جميع المتغيرات مربعة على الأقل. وبالتالي فإن العامل المشترك هو x ² :

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

تذكر أنه عندما يكون العامل المشترك مطابقًا للحد، يجب وضع 1 مكانه.

تمرين 2

خذ بعين الاعتبار العامل المشترك لمتعددات الحدود التالية:

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

انظر الحل

أ) جميع معاملات العناصر التي تشكل كثيرة الحدود الأولى هي مضاعفات العدد 2، لذلك باستخراج العامل المشترك تصبح كثيرة الحدود:

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

ب) في جميع حدود كثيرة الحدود يوجد x واحد على الأقل، وبالتالي:

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

ج) القاسم المشترك الأكبر لمعاملات جميع حدود كثيرة الحدود هو 5، بحيث يكون القاسم المشترك لكثيرة الحدود المذكورة هو 5:

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

د) جميع الحدود في كثيرة الحدود لها x واحد على الأقل، علاوة على ذلك، جميع المعاملات هي مضاعفات 3. لذلك، فإن العامل المشترك لكثيرة الحدود هو 3x:

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

التمرين 3

أوجد العامل المشترك لكل من كثيرات الحدود التالية واطرحه:

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

انظر الحل

أ) جميع أحاديات الحد تحتوي على الحرف على الأقل

$a$

تربيع والحرف

$b$

مكعبة، فالعامل المشترك هو

$a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

ب) جميع معاملات كثيرة الحدود هي مضاعفات 8، علاوة على ذلك، فهي تحتوي على الأقل على x ² وy ² كأجزاء حرفية. وبالتالي فإن العامل المشترك لكثيرة الحدود هو 8x ² y ² .

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

ج) في هذه الحالة، يتطابق العامل المشترك مع قيمة أحادية الحد الوسيطة

$\left(6ab^2c\right)$

، لأن معاملات وحيدات الحد الأخرى هي مضاعفات

$6$

وعلى الاطلاق الجميع

$ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

د) في هذه الحالة بالذات، ليس لدى كثيرة الحدود عامل مشترك، حيث لا يوجد عامل متكرر في جميع حدود كثيرة الحدود. لذلك، لا يمكن تبسيط التعبير متعدد الحدود جبريًا.

$18x^2y+10xy-5xy^3+4z$

التمرين 4

بسّط الكسور الجبرية التالية بأخذ العامل المشترك:

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

انظر الحل

إجراء تبسيط الكسر الجبري، أي الكسر متعدد الحدود، هو استخراج العامل المشترك من بسط ومقام الكسر، ثم حذف العوامل التي تتكرر أعلاه وأدناه. تحت الكسر. لذا:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

التمرين 5

خذ العامل المشترك للتعبيرات متعددة الحدود التالية:

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

انظر الحل

أ) جميع حدود كثيرة الحدود يمكن تحليلها إلى الثالث، وبالتالي:

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

ب) العامل المشترك لكثيرة الحدود داخل الجذر هو 4، لكن يمكننا بعد ذلك إخراج العامل المشترك عن طريق حساب جذره التربيعي:

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

ج) في كثير الحدود هذا يمكننا تطبيق عملية استخراج العامل المشترك عن طريق التجميع:

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

د) جميع المعاملات الكسرية لكثيرة الحدود هي مضاعفات النصف، وبالتالي فإن العامل المشترك لكثيرة الحدود هو ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

👇👇👇 ما رأيك في الشرح؟ هل أحببتها؟ وتذكر أيضًا أنه إذا كانت لديك أي أسئلة حول كيفية تحديد العامل المشترك لكثيرة الحدود أو إذا لم تفهم أحد التمارين، يمكنك دائمًا طرحها علينا في التعليقات، وسنقوم بالرد عليك. 👇👇👇

ما هو العامل المشترك؟

كيفية الحصول على (أو استخراج) العامل المشترك

أمثلة على أخذ (أو استخلاص) العامل المشترك

مثال 1

مثال 2

مثال 3

مثال 4

العامل المشترك للكسور

العامل المشترك حسب التجميع

تمارين العوامل المشتركة تم حلها خطوة بخطوة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد