أنظمة المعادلات هي مجموعات من معادلتين أو أكثر لها أكثر من مجهول. لذا، لحل الأنظمة، يمكننا استخدام أربع طرق: التعويض، المعادلة، التخفيض، والرسوم البيانية. ولكن قبل البدء في شرح إجراءات الحل سنحدد أنواع الأنظمة الموجودة حسب عدد الحلول:
- تحديد النظام المتوافق: له حل واحد فقط ويمكن تمثيله بخطين يتقاطعان في نقطة واحدة (وهو الحل).
- النظام المتوافق غير المحدد: له حلول لا نهائية، وذلك لوجود خطين متطابقين في نفس النقاط.
- النظام غير المتوافق: ليس له حل، لأن الخطوط متوازية وبالتالي لا يوجد أي نقطة مشتركة بينها.
طرق حل أنظمة المعادلات الخطية
سنشرح الآن الأنظمة المختلفة التي يمكننا استخدامها لحل أنظمة المعادلات. ستجد في الشرح النظرية وبعض الأمثلة، والتي بفضلها ستصبح جميع المفاهيم الموضحة أكثر وضوحًا. لاحظ أننا في هذه المقالة سنتحدث فقط عن أنظمة معادلات 2×2 ، مما يعني أننا سنتعامل ببساطة مع أنظمة مكونة من معادلتين. ومع ذلك، فلنبدأ بالشرح.
طريقة الاستبدال
تتكون طريقة الاستبدال من عزل أحد المجهولين في إحدى المعادلات ثم استبدال التعبير الناتج في المعادلة المقابلة. يوصى بهذه الطريقة عندما تكون قيمة المعامل لواحد على الأقل من المجهولات تساوي 1. وبالتالي، فإن الخطوات التي يجب اتباعها بسيطة جدًا:
- اعزل كمية مجهولة من إحدى المعادلتين.
- عوض في المعادلة الأخرى بالتعبير المكافئ للمجهول الذي حذفناه من المعادلة الأولى.
- امسح عكس المجهول في المعادلة التي حصلنا عليها.
- بمجرد أن نحصل على قيمة المتغير الأول، علينا استخدامه للعثور على المتغير الثاني.
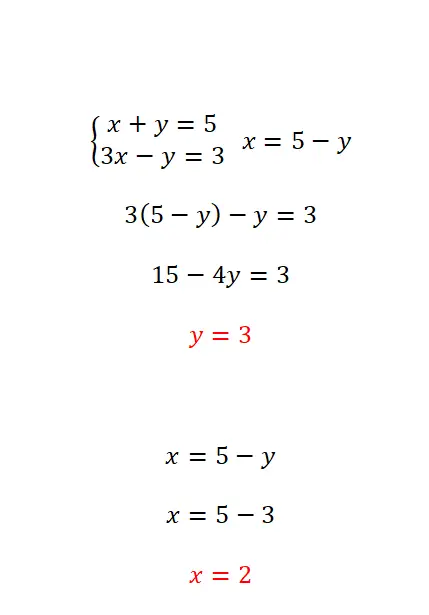
طريقة المعادلة
تتمثل طريقة المطابقة في عزل نفس المتغير في المعادلتين ثم مطابقة التعبيرين اللذين تم الحصول عليهما. يوصى بهذه الطريقة عندما يكون من السهل عزل نفس المجهول في كلتا المعادلتين، حيث أن ذلك يجعل الحساب بأكمله أسهل. الإجراء الذي يجب عليك اتباعه في هذه الحالة هو كما يلي:
- نعزل المجهول الذي اخترناه في المعادلتين.
- نحن نستوعب التعبيرات المكافئة لهذا المجهول.
- نحن نحل المعادلة بشكل طبيعي.
- نحسب المجهول الآخر بالقيمة التي حسبناها.
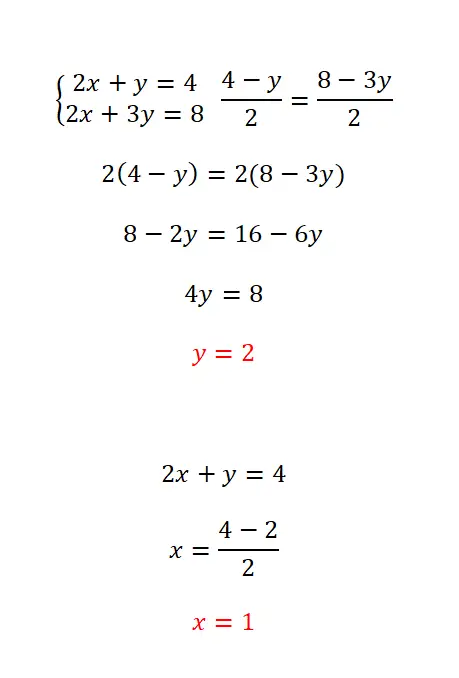
طريقة التخفيض
تعتمد طريقة الاختزال على ضرب المعادلتين في رقمين، مما يتيح لنا الحصول على نفس المعامل مع اختلاف إشارة أحد المتغيرين في كلا التعبيرين. يوصى بهذه الطريقة عندما يكون للمجهول نفسه نفس المعامل في جميع المعادلات أو في حالة وجود نفس معاملات الإشارات المعاكسة. وإجراءات الحل هي كما يلي:
- يتم ضرب المعادلتين بالأرقام الضرورية (عليك إيجاد رقمين يتيحان الحصول على نفس المعامل لأحد المتغيرين في المعادلتين ولكن بإشارة معاكسة).
- ثم يتم طرح المعادلات أو إضافتها لإزالة هذا المجهول بمعاملاتها.
- ثم يتم حل المعادلة المتبقية.
- ونستخدم نتيجة هذه المعادلة للحصول على القيمة العددية المفقودة في المتغير الآخر.
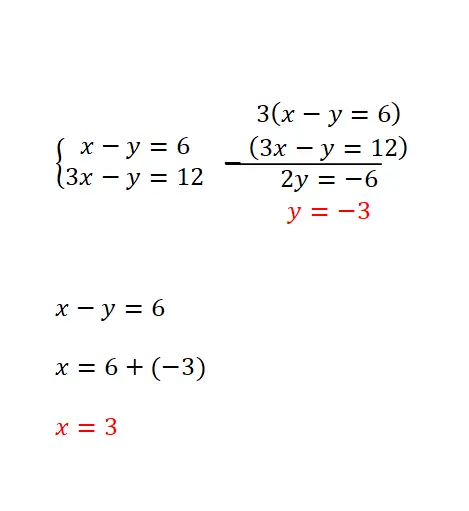
طريقة الرسم
وأخيرا، يمكننا أن نختار حل نظام من المعادلات عن طريق التمثيل البياني . تختلف هذه الطريقة تمامًا عن الطرق الأخرى، لأنها لا تحتوي على جزء رياضي معقد، فهي رسومية بالكامل تقريبًا. وبالتالي، لمعرفة قيم المجهولات يجب أن نبني المعادلتين على شكل معادلة الخط: y = mx + b . وبهذه الطريقة سنتمكن من إجراء التمثيل بعد ذلك، وسنربط قيم إحداثيات نقطة القطع بين الدالتين بالمجهولين. هنا مثال عملي:
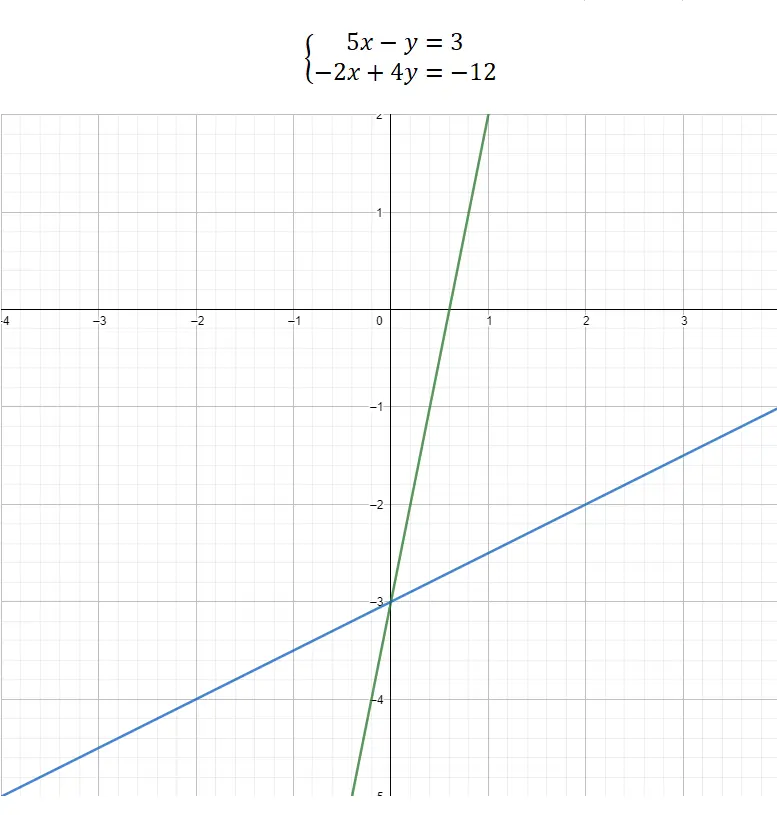
وكما هو واضح في الرسم البياني، فإن النقطة الفاصلة بين الدالتين هي (0، -3). ولذلك فإن قيمة x = 0 وقيمة y = -3. هذه هي الطريقة التي يتم بها حل نظام المعادلات بيانيا.
كيفية حل نظام المعادلات التربيعية؟
لحل أنظمة المعادلات التربيعية، يمكننا استخدام الطرق التي ناقشناها للتو. شخصيًا، نود أن نوصي بطريقة الاستبدال لأنها تتيح لنا الحصول بسرعة على معادلة ذات مجهول واحد. من ناحية أخرى، إذا استخدمنا طرق التخفيض أو المعادلة، يصبح الحساب معقدًا للغاية. لذا، بمجرد قيامك بالتعويض بأحد المتغيرين، ما عليك سوى حل المعادلة التربيعية الناتجة أو المعادلة التربيعية . إليك مثال حتى تتمكن من رؤية العملية برمتها:
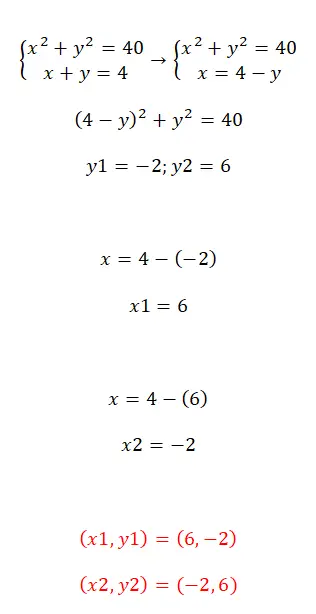
تمارين على حل أنظمة المعادلات
نقدم لك الآن بعض التمارين على أنظمة المعادلات الخطية والتربيعية حتى تتمكن من تطبيق النظرية الموضحة. بهذه الطريقة ستفهم بشكل أفضل جميع المفاهيم المتعلقة بحساب أنظمة المعادلات. ننصحك بمحاولة حلها قبل الاطلاع على الإجابات التي نقدمها، وبهذه الطريقة ستحقق أقصى استفادة من التمارين:
التمرين 1
حل نظام المعادلات هذا باستخدام طريقة الاستبدال:
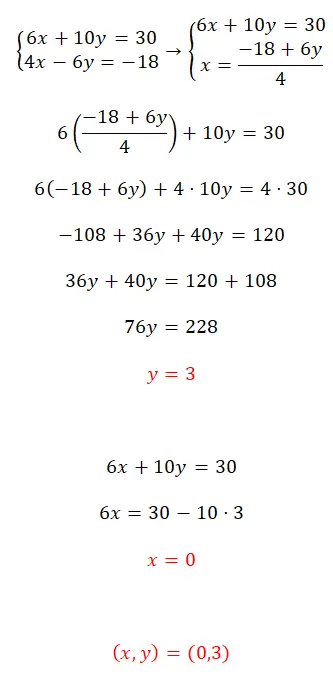
- نبدأ بعزل أحد المجهولين في المعادلة.
- ثم نعوض التعبير الناتج في المعادلة المقابلة بالمجهول الذي حلله سابقًا.
- ثم نحصل على نتيجة المتغير المعاكس.
- بعد ذلك، نعوض بالقيمة المكتشفة الأولى في إحدى المعادلتين لحساب قيمة المجهول الأول.
- وأخيرا، نعبر عن نتيجة المتغيرين.
تمرين 2
حل نظام المعادلات هذا باستخدام طريقة الاستبدال:
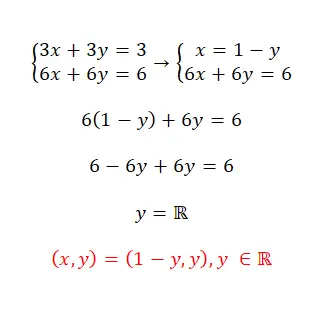
- في هذه الحالة سوف نتبع نفس الإجراء: عزل مجهول، واستبداله في التعبير الآخر وعزل المتغير الثاني.
- كما نرى، هذا نظام متوافق غير محدد، لأنه يحتوي على عدد لا نهائي من الحلول.
التمرين 3
حل نظام المعادلات هذا باستخدام طريقة المعادلة:
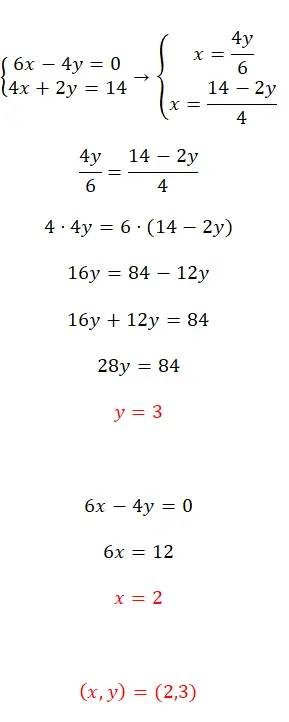
- الخطوة الأولى هي عزل نفس المتغير في كلتا المعادلتين، وفي هذه الحالة اخترنا x.
- ثم نطابق التعبيرات الناتجة ونبدأ في حلها.
- وبذلك نحصل على قيمة المجهول الأول.
- وإذا عوضنا بها في إحدى المعادلتين الأصليتين، فيمكننا حساب المجهول الثاني.
- وأخيرا، نعبر عن نتيجة المتغيرين.
التمرين 4
حل نظام المعادلات هذا باستخدام طريقة المعادلة:
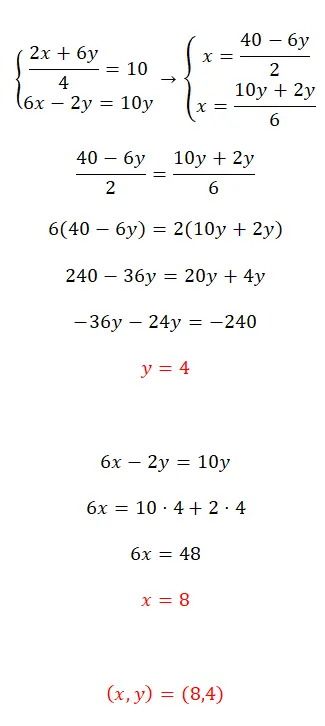
- أولا، نعزل x في كلتا المعادلتين.
- بعد ذلك، نقوم بمطابقة التعبيرات التي حصلنا عليها.
- نحصل على قيمة المجهول الأول.
- نعوض بهذه القيمة في إحدى المعادلتين الأوليتين ونحسب المجهول الثاني.
- وأخيراً نعبر عن قيمة الغريبين.
التمرين 5
حل نظام المعادلات هذا باستخدام طريقة التخفيض:
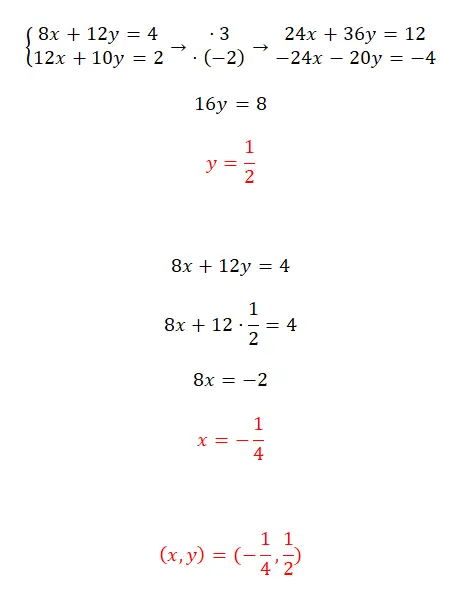
- عليك أن تبحث عن رقمين يتيحان الحصول على نفس المعامل لأحد المتغيرين في المعادلتين ولكن بإشارة معاكسة .
- ثم، ما عليك سوى حل المعادلة التي نحصل عليها عن طريق إضافة التعبيرين اللذين تم الحصول عليهما.
- بعد ذلك، نعوض بـ y في إحدى المعادلتين الأصليتين لحساب x.
- وأخيرا، نعبر عن نتيجة النظام.
التمرين 6
حل نظام المعادلات هذا باستخدام طريقة التخفيض:
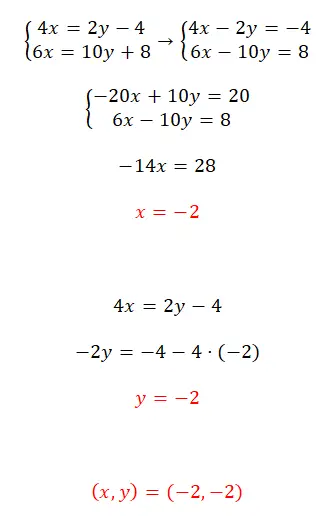
- نبدأ بترتيب المعادلات (تمرير جميع المتغيرات إلى اليسار).
- ثم نضرب المعادلة الأولى في -5.
- نحل المعادلة التي نحصل عليها بجمع المعادلتين ونحصل على قيمة x.
- نستخدم هذه القيمة المعروفة للحصول على قيمة y.
- نعبر عن نتيجة نظام المعادلات.
التمرين 7
حل نظام المعادلات هذا باستخدام طريقة الاستبدال:
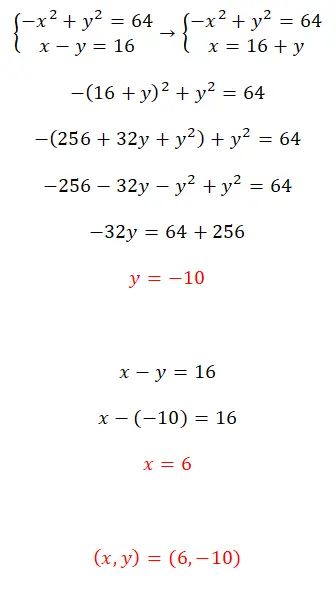
- لحل هذا النظام من المعادلات غير الخطية، نوصي باستخدام طريقة الاستبدال.
- لذلك تقوم بإنشاء معادلة بالتعبير المكافئ لـ x.
- تحصل على قيمة المجهول y.
- يمكنك حساب قيمة x بالقيمة التي حسبتها مسبقًا.
- ولديك بالفعل كلتا القيمتين.
التمرين 8
حل نظام المعادلات هذا باستخدام الطريقة التي تختارها:
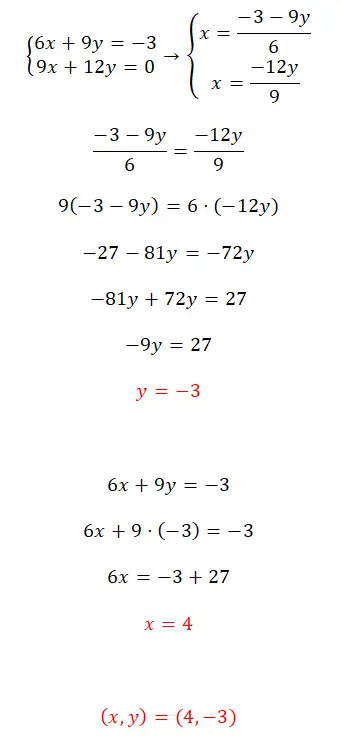
- في هذه الحالة، أمامنا نظام متوافق محدد وسنقوم بحله باستخدام طريقة المعادلة.
- ولذلك، فإننا نحل قيمة x في كلتا المعادلتين ونجعل التعبيرين الناتجين متساويين.
- وبعد حل المعادلة نحصل على قيمة y.
- نستخدم هذه القيمة لإيجاد قيمة x.
- وأخيرا، نعبر عن نتيجة النظام.