مصفوفة غير متماثلة

في هذه الصفحة نشرح ما هي المصفوفات غير المتماثلة. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة بالإضافة إلى بنيتها النموذجية لفهمها بشكل مثالي. نوضح أيضًا خصوصية حساب محدد المصفوفة غير المتماثلة وجميع خصائص هذا النوع من المصفوفات. وأخيرًا، ستكتشف كيفية تحليل أي مصفوفة مربعة إلى مجموع مصفوفة متماثلة بالإضافة إلى مصفوفة أخرى غير متماثلة.

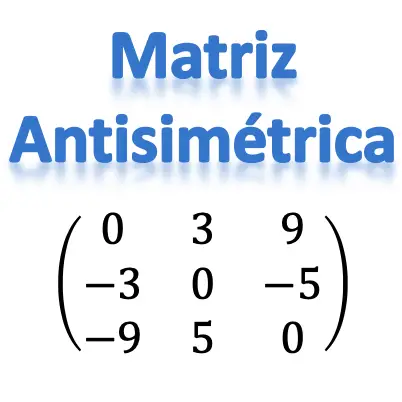
ما هي المصفوفة غير المتماثلة؟

تعريف المصفوفة غير المتماثلة هو كما يلي:

المصفوفة غير المتماثلة هي مصفوفة مربعة يكون تبديلها مساويًا لسالب المصفوفة.

$A^t = -A$

ذهب

$A^t$

يمثل المصفوفة المنقولة

$A$

$-A$

هي المصفوفة

$A$

مع تغير جميع عناصره علامة.

أمثلة على المصفوفات غير المتماثلة

بمجرد أن تعرفنا على مفهوم المصفوفة غير المتماثلة، سنرى عدة أمثلة على المصفوفات غير المتماثلة لفهمها بشكل أفضل:

مثال لمصفوفة غير متماثلة من الرتبة 2 × 2

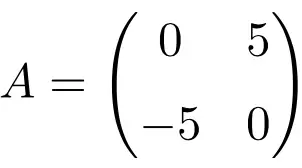
مثال على المصفوفة غير المتماثلة ذات البعد 2x2

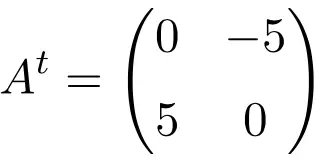
تمرين محلول على المصفوفة غير المتماثلة ذات البعد 2x2

مثال لمصفوفة غير متماثلة البعد 3×3

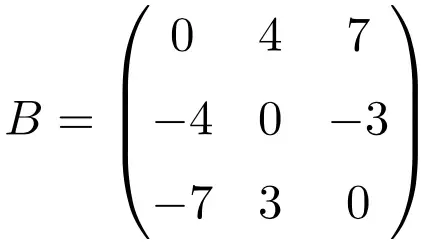
مثال على مصفوفة غير متماثلة ذات البعد 3x3

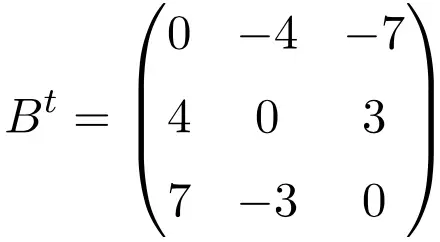
تمرين محلول على المصفوفة غير المتماثلة ذات البعد 3x3

مثال لمصفوفة غير متماثلة بحجم 4×4

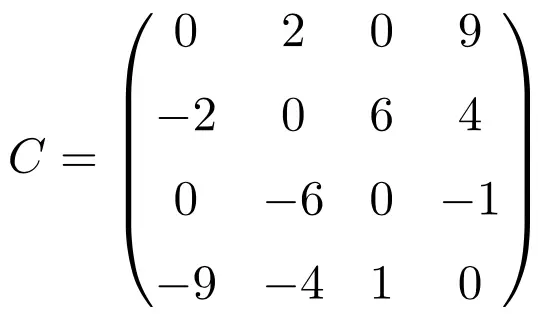
مثال على المصفوفة غير المتماثلة ذات البعد 4x4

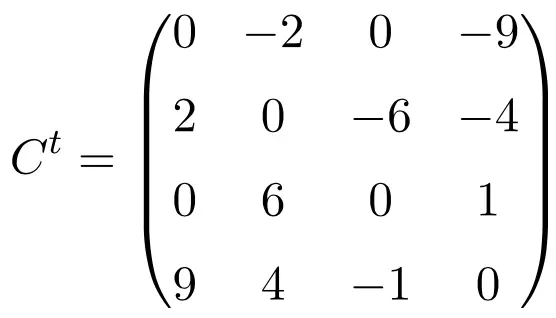
تمرين محلول على المصفوفة غير المتماثلة ذات البعد 4x4

عند تبديل هذه المصفوفات الثلاث، نتحقق من أنها غير متماثلة، لأن المصفوفات المنقولة تعادل إشارة تغير المصفوفات الأصلية الخاصة بها.

هيكل مصفوفة غير متماثلة

لكي يتم استيفاء شرط المصفوفة غير المتماثلة، يجب أن يكون لها دائمًا نفس النوع من البنية: الأرقام الموجودة على القطر الرئيسي كلها تساوي الصفر وعنصر الصف i والعمود j هو سالب عنصر الصف j والعمود أنا . بمعنى آخر، يكون شكل المصفوفات غير المتماثلة كما يلي:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

ولذلك، فإن القطر الرئيسي للمصفوفة غير المتماثلة يعمل كمحور لعدم التماثل. ومن هنا يأتي اسم هذه المصفوفة بالذات.

محدد المصفوفة غير المتماثلة

يعتمد محدد المصفوفة غير المتماثلة على أبعاد المصفوفة المذكورة. ويرجع ذلك إلى خصائص المحددات:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

وبالتالي، إذا كانت المصفوفة غير المتماثلة ذات ترتيب فردي، فإن محددها سيكون مساوياً للصفر . من ناحية أخرى، إذا كانت المصفوفة غير المتماثلة ذات أبعاد زوجية، فيمكن للمحدد أن يأخذ أي قيمة.

ولذلك، فإن المصفوفة غير المتماثلة ذات البعد الفردي هي مصفوفة مفردة أو منحلة. من ناحية أخرى، المصفوفة غير المتماثلة ذات الترتيب الزوجي هي مصفوفة منتظمة.

خصائص المصفوفات غير المتماثلة

خصائص المصفوفات غير المتماثلة هي كما يلي:

إن إضافة (أو طرح) مصفوفتين غير متماثلتين يعطي مصفوفة أخرى غير متماثلة. نظرًا لأن نقل مصفوفتين مضافتين (أو مطروحتين) يعادل نقل كل مصفوفة على حدة:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

أي مصفوفة غير متماثلة مضروبة في عددية تؤدي أيضًا إلى ظهور مصفوفة أخرى غير متماثلة.

قوة المصفوفة غير المتماثلة تعادل مصفوفة غير متماثلة أو مصفوفة متماثلة. إذا كان الأس رقمًا زوجيًا، فإن نتيجة الأس هي مصفوفة متماثلة، ولكن إذا كان الأس عددًا فرديًا، فإن نتيجة الأس هي مصفوفة غير متماثلة. يمكنك استشارة في هذا الرابطما هي المصفوفة المتماثلة .

إن أثر المصفوفة غير المتماثلة يساوي دائمًا الصفر.

مجموع أي مصفوفة غير متماثلة بالإضافة إلى المصفوفة الوحدوية يؤدي إلى مصفوفة مقلوبة.

$\displaystyle \text{det}(A+I)\neq 0$

جميع القيم الذاتية الحقيقية (أو القيم الذاتية) للمصفوفة غير المتماثلة هي 0. ومع ذلك، يمكن أن تحتوي المصفوفة غير المتماثلة أيضًا على قيم ذاتية معقدة.

جميع المصفوفات غير المتماثلة هي مصفوفات عادية. لذلك، فهي تخضع للنظرية الطيفية، التي تنص على أنه يمكن قطري المصفوفة غير المتماثلة بواسطة مصفوفة وحدوية.

تحلل المصفوفة المربعة إلى مصفوفة متماثلة ومصفوفة غير متماثلة

الميزة الخاصة للمصفوفات المربعة هي أنها يمكن أن تتحلل إلى مجموع مصفوفة متماثلة بالإضافة إلى مصفوفة غير متماثلة.

الصيغة التي تسمح لنا بالقيام بذلك هي كما يلي:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

حيث C هي المصفوفة المربعة التي نريد تحليلها، C ^t تبديلها، وأخيرًا S و A هما على التوالي المصفوفات المتماثلة وغير المتماثلة التي تتحلل فيها المصفوفة C.

يوجد أدناه تمرين تم حله لتوضيح الصيغة. دعونا نحلل المصفوفة التالية:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

نحسب المصفوفة المتماثلة وغير المتماثلة بالصيغ:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

ويمكننا التأكد من تحقق المعادلة عن طريق جمع المصفوفتين:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅