مصفوفات متشابهة أو متشابهة

ستجد في هذه الصفحة شرح المصفوفات المتشابهة، وتسمى أيضًا المصفوفات المتشابهة. علاوة على ذلك، نعرض لك مثالا واضحا لمصفوفتين متشابهتين وجميع خصائص هذا النوع من المصفوفات حتى لا يكون لديك أي شك. وأخيرًا، ستتمكن أيضًا من رؤية كيفية ارتباطها بالمصفوفات المتطابقة.

ما هي المصفوفات المتشابهة (أو المشابهة)؟

تعريف المصفوفات المماثلة هو كما يلي:

مصفوفتان

$A$

$B$

متشابهة (أو متشابهة) إذا كانت هناك مصفوفة

$P$

والذي يتحقق فيه الشرط التالي:

$P^{-1}AP = B$

أو ما يعادلها:

$AP = PB$

في الواقع، المصفوفة

$P$

بمثابة مصفوفة التغيير الأساسية. إذن، ما تعنيه هذه المعادلة هو المصفوفة

$A$

يمكن التعبير عنها في قاعدة أخرى (

$P$

)، مما يؤدي إلى المصفوفة

$B$

يمكن أيضًا تسمية هذا المصطلح بتحويل التشابه ، نظرًا لأننا نقوم بالفعل بتحويل المصفوفة

$A$

في المصفوفة

$B$

ومن الواضح أن المصفوفة

$P$

يجب أن تكون مصفوفة منتظمة أو غير منحلة (محدد غير صفري).

ومن ناحية أخرى يمكننا أن نشير إلى أن مصفوفتين متشابهتين بالتعبير التالي:

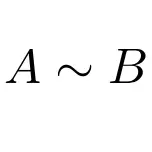
تعتبر هذه الفئة من المصفوفات أكثر أهمية مما تبدو بالنسبة للجبر الخطي. يتم استخدامها بشكل أساسي للمصفوفات القابلة للقطر، لأن الإجراء الخاص بقطر أي مصفوفة يعتمد على مفهوم تشابه المصفوفة.

في الواقع، تتضمن عملية تحديد المصفوفة بشكل قطري حساب مصفوفة مماثلة تكون في نفس الوقت مصفوفة قطرية. يمكنك أن ترى كيف يتم ذلك في كيفية جعل المصفوفة قطرية .

مثال على مصفوفات مماثلة أو مماثلة

ثم سنرى مثالاً لمصفوفات مماثلة ذات البعد 2×2 لإنهاء استيعاب المفهوم.

تتشابه المصفوفتان المربعتان A وB مع بعضهما البعض من خلال المصفوفة القابلة للعكس P:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

لإثبات أن هذه المصفوفات متشابهة، يجب علينا أولاً حساب المصفوفة العكسية لـ P:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

والآن نتحقق من تشابههما عن طريق إجراء ضرب المصفوفة الذي يحدد تشابه المصفوفتين:

$\displaystyle P^{-1}AP = B \quad ?$

$\displaystyle P^{-1}AP = B$

✅

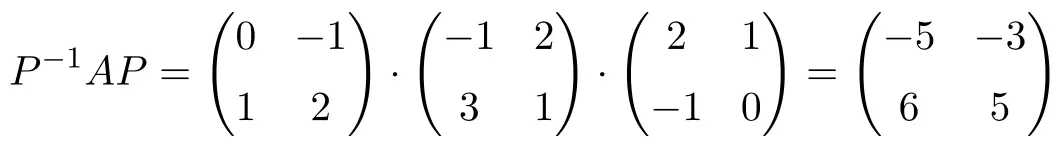
نعم، لقد تحققت علاقة التشابه، فهي مصفوفات متشابهة.

خصائص المصفوفة مماثلة

تشترك مصفوفتان متشابهتان A وB في الخصائص التالية:

نفس الرتبة.

$rg(A)=rg(B)$

محددات المصفوفتين هي نفسها.

$det(A)=det(B)$

نفس التتبع.

$tr(A)=tr(B)$

نفس القيم الذاتية (أو القيم الذاتية). ومع ذلك، فإن المتجهات الذاتية (أو المتجهات الذاتية) عادة ما تكون مختلفة.

نفس كثير الحدود المميزة والحد الأدنى متعدد الحدود.

نقل المصفوفة يشبه المصفوفة الأصلية.

يمكن العثور على المصفوفة B من خلال تطبيق العمليات الأولية على صفوف المصفوفة A، والعكس صحيح.

ومن الواضح أن التشابه ينعكس. أي أنه إذا كان A يشبه B، فإن B يشبه A أيضًا.

علاوة على ذلك، فإن تشابه المصفوفات يكون متماثلًا أيضًا. بمعنى آخر، إذا كان من الممكن الحصول على المصفوفة المشابهة للمصفوفة A (B) باستخدام المصفوفة P، فيمكن أيضًا الحصول على المصفوفة المشابهة للمصفوفة B (A) بنفس المصفوفة P:

$B=P^{-1}AP$

$A=PBP^{-1}$

وعلاوة على ذلك، فإن التشابه هو متعدية. لذا، إذا كانت المصفوفة A تشبه المصفوفة B والمصفوفة B تشبه المصفوفة C، فإن المصفوفة A تشبه أيضًا المصفوفة C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

وأخيرًا، كل قالب يشبه قالب مسنن. ومن هذه الخاصية يمكننا أن نستنتج النتيجة الطبيعية التالية: كل مصفوفة مربعة تشبه المصفوفة الثلاثية.

المصفوفات المتطابقة

من ناحية أخرى، هناك أيضًا علاقة أخرى مشابهة جدًا بين المصفوفات، ولكن بدلاً من أن تكون مع المصفوفة العكسية، فهي مع مصفوفة النقل. وهذا ما يسمى التطابق .

تتطابق المصفوفتان A وB إذا كانت هناك مصفوفة قابلة للعكس P والتي تتحقق معها المساواة التالية:

$P^tAP = B$

كما ترون، هذا هو التناظرية لمصفوفات مماثلة ولكن مع نقل المصفوفة.

ما هي المصفوفات المتشابهة (أو المشابهة)؟

مثال على مصفوفات مماثلة أو مماثلة

خصائص المصفوفة مماثلة

المصفوفات المتطابقة

اترك تعليقاً إلغاء الرد