مصفوفة متعامدة

في هذه الصفحة ستشاهد ما هي المصفوفات المتعامدة والعلاقة بينها وبين معكوس المصفوفة. سترى أيضًا العديد من الأمثلة لفهمها تمامًا. بالإضافة إلى ذلك، فإننا نعلمك الصيغة التي تتحقق من أي مصفوفة متعامدة، والتي ستعرف من خلالها كيفية العثور على مصفوفة بسرعة. وأخيرًا، ستجد خصائص وتطبيقات هذه المصفوفات المحددة بالإضافة إلى تمرين نموذجي للامتحان.

ما هي المصفوفة المتعامدة؟

تعريف المصفوفة المتعامدة هو كما يلي:

المصفوفة المتعامدة هي مصفوفة أعداد حقيقية مربعة، مضروبة في منقولها (أو منقولها) يساوي مصفوفة الهوية. أي أن الشرط التالي قد تحقق:

$A\cdot A^t = A^t \cdot A =I$

ذهب

$A$

هي مصفوفة متعامدة و

$A^t$

يمثل المصفوفة المنقولة.

لكي يتم استيفاء هذا الشرط، يجب أن تكون أعمدة وصفوف المصفوفة المتعامدة عبارة عن متجهات وحدة متعامدة، أي أنها يجب أن تشكل أساسًا متعامدًا. لهذا السبب، يطلق عليها بعض علماء الرياضيات أيضًا المصفوفات المتعامدة .

معكوس المصفوفة المتعامدة

هناك طريقة أخرى لشرح مفهوم المصفوفة المتعامدة وهي من خلال المصفوفة العكسية، لأن مصفوفة النقل (أو النقل) للمصفوفة المتعامدة تساوي معكوسها.

لفهم هذه النظرية بشكل كامل، من المهم أن تعرف كيفية قلب المصفوفة . ستجد في هذا الرابط شرحًا تفصيليًا لمقلوب المصفوفة، وجميع خصائصها، بالإضافة إلى تمارين تم حلها خطوة بخطوة للتدرب عليها.

يمكن بسهولة إظهار المصفوفة العكسية للمصفوفة المتعامدة على أنها مكافئة لتبديلها باستخدام حالة المصفوفة المتعامدة والخاصية الرئيسية للمصفوفات العكسية:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

ولذلك، فإن المصفوفة المتعامدة ستكون دائمًا مصفوفة قابلة للعكس ، أو بمعنى آخر، ستكون مصفوفة عادية أو غير متدهورة.

بعد ذلك، سنرى عدة أمثلة للمصفوفات المتعامدة لإنهاء فهم مفهوم كل شيء.

مثال على مصفوفة متعامدة 2×2

المصفوفة التالية هي مصفوفة متعامدة البعد 2×2:

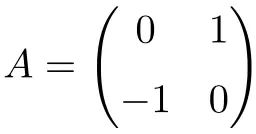
يمكننا التحقق من أنه متعامد عن طريق حساب المنتج من خلال تبديله:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

وبما أن النتيجة تعطي مصفوفة متطابقة، فإننا نتحقق من أن A هي مصفوفة متعامدة.

مثال على مصفوفة متعامدة 3×3

المصفوفة التالية هي مصفوفة متعامدة البعد 3×3:

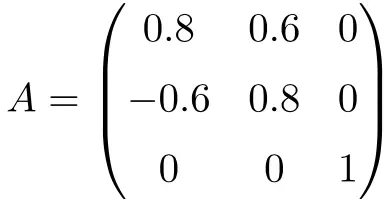
يمكننا أن نبين أنها متعامدة عن طريق ضرب المصفوفة A في منقولها:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

بما أن الحل هو المصفوفة الوحدوية، نوضح أن A هي مصفوفة متعامدة.

صيغة لإيجاد مصفوفة متعامدة 2×2

سنرى بعد ذلك الدليل على أن جميع المصفوفات المتعامدة من الرتبة 2 تتبع نفس النمط.

خذ بعين الاعتبار مصفوفة عامة بحجم 2 × 2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

لكي تكون هذه المصفوفة متعامدة، يجب تحقيق معادلة المصفوفة التالية:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

وبحل عملية ضرب المصفوفات نحصل على المعادلات التالية:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

إذا نظرت عن كثب، فإن هذه التساويات تشبه إلى حد كبير العلاقة المثلثية الأساسية فيثاغورس :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

وبالتالي، فإن المصطلحات التي تحقق المعادلتين (1) و(3) التي تم الحصول عليها هي:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

بالإضافة إلى ذلك، من خلال استبدال القيم في المعادلة الثانية، نحصل على العلاقة بين الزاويتين:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

أي أنه يجب توافر أحد الشرطين التاليين:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

لذا، في الختام، يجب أن يكون للمصفوفات المتعامدة بنية إحدى المصفوفتين التاليتين:

ذهب

$\theta$

هو عدد حقيقي.

في الواقع، إذا كمثال نمنح القيمة

$\displaystyle\theta=\frac{\pi}{2}$

ونأخذ البنية الأولى، سنحصل على المصفوفة التي تحققنا من أنها متعامدة في قسم “مثال على مصفوفة متعامدة 2×2”:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

خصائص المصفوفة المتعامدة

خصائص هذا النوع من المصفوفات هي:

لا يمكن للمصفوفة المتعامدة أن تكون مصفوفة مفردة أبدًا، لأنها يمكن أن تكون مقلوبة دائمًا. وبهذا المعنى، فإن معكوس المصفوفة المتعامدة هو مصفوفة متعامدة أخرى.

يمكن قطري أي مصفوفة متعامدة. نقول بعد ذلك أن المصفوفات المتعامدة قابلة للقياس قطريًا.

جميع القيم الذاتية أو القيم الذاتية للمصفوفة المتعامدة لها معامل يساوي 1.

أي مصفوفة متعامدة تتكون فقط من أرقام حقيقية هي أيضًا مصفوفة عادية.

التناظرية للمصفوفة المتعامدة في بيئة ذات أرقام مركبة هي المصفوفة الوحدوية.

من الواضح أن مصفوفة الهوية هي مصفوفة متعامدة.

مجموعة المصفوفات المتعامدة ذات البعد n × n وكذلك تشغيل منتج المصفوفة تشكل مجموعة تسمى المجموعة المتعامدة. أي أن حاصل ضرب مصفوفتين متعامدتين يساوي مصفوفة متعامدة أخرى.

بالإضافة إلى ذلك، يمكن التعبير عن نتيجة ضرب المصفوفة المتعامدة في منقولها بواسطة دلتا كرونيكر:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

وأخيرًا، محدد المصفوفة المتعامدة يكون دائمًا +1 أو -1.

$\displaystyle \text{det}(A)=\pm 1$

حل تمرين المصفوفات المتعامدة

وسنقوم بعد ذلك بحل تمرين على المصفوفات المتعامدة.

بالنظر إلى المصفوفة المربعة التالية من الرتبة 3، أوجد قيم
$a$

و

$b$

لجعلها متعامدة:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

لكي يتم تحقيق تعامد المصفوفة، يجب أن يكون منتج المصفوفة من خلال تبديلها مساويًا لمصفوفة الهوية. لذا:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

نضرب المصفوفات:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

يمكننا الآن الحصول على معادلة من الزاوية العلوية اليسرى من المصفوفات، لأن العناصر الموجودة في هذا الموضع يجب أن تتطابق. حتى الآن:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

نحل المعادلة ونحذف المجهول:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

لكن هناك معادلات لا تصمد مع الحل الموجب، مثلاً تلك الموجودة في الزاوية اليمنى العليا. لذا فإن الحل السلبي فقط هو الممكن .

ومن ناحية أخرى، لحساب المتغير

$b$

يمكننا، على سبيل المثال، مطابقة المصطلحات الموضوعة في الصف الثاني من العمود الأول:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

عن طريق استبدال قيمة

$a$

في المعادلة:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

باختصار الحل الوحيد الممكن هو:

$\displaystyle \bm{a=b =-2}$

إذن المصفوفة المتعامدة التي تقابل هذه القيم هي:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

تطبيقات المصفوفات المتعامدة

على الرغم من أن الأمر قد لا يبدو كذلك لأنها عادةً ما تكون ذات شكل بسيط جدًا، إلا أن المصفوفات المتعامدة مهمة جدًا في الرياضيات، خاصة في مجال الجبر الخطي.

في الهندسة، تمثل المصفوفات المتعامدة تحويلات متساوية القياس (التي لا تغير المسافات والزوايا) في فضاءات متجهة حقيقية، ولهذا السبب تسمى التحولات المتعامدة. علاوة على ذلك، فإن هذه التحولات هي تماثلات داخلية لمساحة المتجه قيد النظر. يمكن أن تكون هذه التحولات عبارة عن دورات أو انعكاسات مرآوية أو انقلابات .

وأخيرا، يستخدم هذا النوع من المصفوفات أيضا في الفيزياء، لأنه يسمح بدراسة حركة الأجسام الصلبة. بل إنها تستخدم في صياغة بعض النظريات الميدانية.