نقاط متحدة المستوى (أو متحدة المستوى)

ستكتشف في هذه الصفحة ما هي النقاط المستوية (أو المستوية) وكيفية معرفة ما إذا كانت بعض النقاط متحدة المستوى أم لا. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على حل تمارين النقاط المستوية.

ما هي النقاط المستوية؟

في الهندسة التحليلية، يكون معنى النقاط المستوية (أو المستوية) كما يلي:

النقاط المستوية هي النقاط التي تنتمي إلى نفس المستوى.

لذلك، تكون النقطتان أو الثلاث دائمًا مستوية لأنه يمكن تشكيل المستوى بعدد قليل يصل إلى 3 نقاط. من ناحية أخرى، عندما يكون هناك 4 أو 5 نقاط أو أكثر، فمن الممكن ألا تكون بعض النقاط موجودة في نفس المستوى، وبالتالي فهي ليست مستوية.

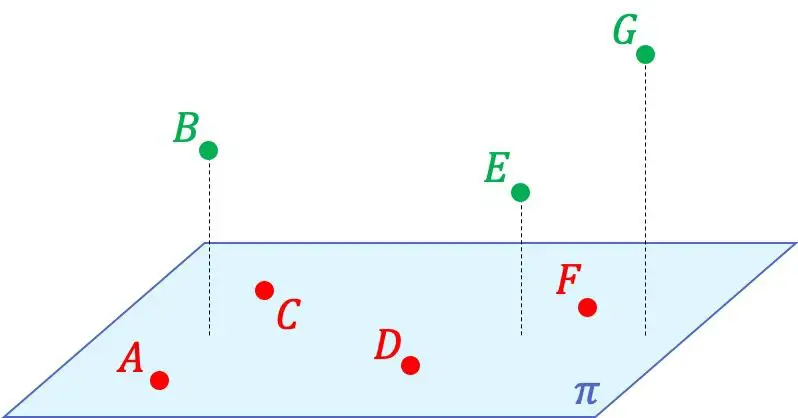
على سبيل المثال، في التمثيل البياني أعلاه، يمكنك أن ترى أن النقاط A وC وD وF متحدة المستوى مع بعضها البعض، لأنها موجودة في نفس المستوى. ومن ناحية أخرى، فإن هذه النقاط الأربع ليست مستوية مع النقاط B وE وG، لأنه لا يمكن تشكيل أي مستوى في الفضاء الذي يحتوي على جميع النقاط.

من هذه الخاصية، يمكننا أن نستنتج أن المتجهات المحددة بنقاط مستوية هي أيضًا متجهات مستوية، أي أنها موجودة في نفس المستوى.

متى تكون النقاط مستوية؟

كما رأينا في تعريف النقاط المستوية (أو المستوية)، تكون نقطتان أو ثلاث نقاط دائمًا متحدة المستوى، ولكن ليس من الضروري أن تحترم أكثر من ثلاث نقاط العلاقة المستوية.

لذلك، هناك طريقتان أساسيتان لتحديد ما إذا كانت أربع نقاط أو أكثر مستوية:

إحدى الطرق لمعرفة ما إذا كانت النقاط متحدة المستوى هي عن طريق المتجهات التي تحددها النقاط: إذا كانت هذه المتجهات متحدة المستوى ، فإن النقاط أيضًا متحدة المستوى.

من الواضح، لتطبيق هذه الطريقة، عليك أن تعرف متى تكون المتجهات متحدة المستوى. ولكن نظرًا لوجود عدة طرق أيضًا لتحديد ما إذا كانت مجموعة المتجهات متحدة المستوى، نوصي بمراجعة كيفية معرفة ما إذا كانت المتجهات متحدة المستوى . ستجد هنا جميع الإجراءات الموجودة لمعرفة متى يكون 2، 3، 4 أو أكثر من المتجهات متحدة المستوى، بالإضافة إلى أمثلة وتمارين تم حلها.

هناك طريقة أخرى لمعرفة ما إذا كانت مجموعة من النقاط متحدة المستوى، وهي إيجاد معادلة المستوى المتكون من 3 نقاط في المجموعة، وإذا كانت النقاط الأخرى تحقق هذه المعادلة، فهذا يعني أن جميع النقاط في المجموعة متحدة المستوى.

على الرغم من أن ذلك يعتمد على المشكلة، إلا أننا نوصي باستخدام الطريقة الأولى من الطريقتين، لأنه من الأسهل والأسرع التحقق مما إذا كانت المتجهات متحدة المستوى بدلاً من حساب معادلة المستوى. ولكن من الواضح أن استخدام ما تفضله.

حل مشاكل نقطة متحد المستوى

التمرين 1

حدد ما إذا كانت النقاط الثلاث التالية مستوية أم لا:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

انظر الحل

في هذه الحالة ليس من الضروري القيام بأي حسابات لأن النقاط الثلاث تكون دائمًا مستوية ، مهما كانت.

تمرين 2

حدد ما إذا كانت النقاط الأربع التالية متحدة المستوى:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

انظر الحل

لكي تكون النقاط الأربع متحدة المستوى، يجب أن تكون المتجهات المحددة بها متحدة المستوى. لذلك نحسب هذه المتجهات:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

دعونا الآن نبني المصفوفة التي شكلتها المتجهات:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

لكي تكون المتجهات الناتجة مستوية، يجب أن تكون رتبة المصفوفة السابقة مساوية لـ 2. ولهذا، يجب أن يكون محدد المصفوفة 3×3 بأكملها مساويًا للصفر:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

ومع ذلك، فإن محدد المصفوفة بأكملها غير صفر، وبالتالي فإن رتبة المصفوفة هي 3، وبالتالي فإن النقاط الأربع ليست مستوية .

التمرين 3

اكتشف ما إذا كانت النقاط الخمس التالية متحدة المستوى:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

انظر الحل

لكي تكون جميع النقاط الخمس متحدة المستوى، يجب أن تكون المتجهات التي تحددها متحدة المستوى. لذلك نحسب هذه المتجهات:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

دعونا الآن نبني المصفوفة المكونة من المتجهات:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

لكي تكون المتجهات الناتجة متحدة المستوى، يجب أن تكون رتبة المصفوفة السابقة مساوية لـ 2. لذلك نحسب رتبة مصفوفة المتجهات بواسطة المحددات للتحقق مما إذا كانت متحدة المستوى:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

رتبة المصفوفة تعادل 2، وبالتالي فإن المتجهات هي مستوية وبالتالي فإن النقاط الخمس هي أيضا مستوية.

التمرين 4

حساب قيمة المعلمة

$k$

بحيث تكون النقاط الأربع التالية مستوية:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

انظر الحل

لكي تكون النقاط الأربع متحدة المستوى، يجب أن تكون المتجهات المحددة بها متحدة المستوى. لذلك نحسب هذه المتجهات:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

مصفوفة المتجهات هي:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

لكي تكون المتجهات الناتجة متحدة المستوى، يجب أن تكون رتبة المصفوفة 2. وبالتالي، يجب أن يكون محدد المصفوفة 3×3 بأكملها 0:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

وأخيراً، نحل المجهول

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

أخيرًا، إذا كانت هذه المقالة مفيدة لك، فمن المحتمل أنك مهتم أيضًا بكيفية حساب المسافة بين نقطتين (الصيغة) ، لأنه في بعض الأحيان في مسائل الهندسة التحليلية نسأل ما هي المسافة بين نقطتين. ستجد في الصفحة المرتبطة شرحًا مفصلاً للغاية، بالإضافة إلى أمثلة وتمارين تم حلها خطوة بخطوة.

نقاط متحدة المستوى (أو متحدة المستوى).

ما هي النقاط المستوية؟

متى تكون النقاط مستوية؟

حل مشاكل نقطة متحد المستوى

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد