قاعدة متوازي الأضلاع أو القانون

ستجد في هذه الصفحة شرحًا لقاعدة (أو قانون) متوازي الأضلاع. بالإضافة إلى ذلك، سترى العديد من الأمثلة على جمع المتجهات وطرحها باستخدام قاعدة متوازي الأضلاع، بالإضافة إلى التطبيقات الواقعية.

ما هي قاعدة متوازي الأضلاع؟

كما تعلم بالفعل، لا يمكن جمع الكميات المتجهة أو طرحها بنفس طريقة جمع الأعداد الحقيقية، لأنها تحتوي على مكونين (في R2) أو 3 مكونات (في R3) ولأن المتجهات يمكن أن يكون لها اتجاهات مختلفة. ولذلك، هناك حاجة إلى طرق أخرى لإجراء العمليات المتجهة، مثل قاعدة متوازي الأضلاع، والتي تتكون من ما يلي:

في الرياضيات، قاعدة متوازي الأضلاع هي إجراء لإضافة أو طرح متجهين من تمثيلهما البياني.

من المؤكد أن طريقة متوازي الأضلاع هي الأكثر استخدامًا في جمع وطرح المتجهات (بيانيًا)، لأنها تقنية سهلة الاستخدام للغاية. على سبيل المثال، في الفيزياء يتم استخدامه لجمع وطرح القوى.

من ناحية أخرى، تختلف القاعدة قليلاً اعتمادًا على ما إذا كنا نريد جمع المتجهات أو طرحها، لذا سنشرح أدناه كلا الإصدارين بشكل منفصل.

قاعدة متوازي الأضلاع لإضافة متجهين

إذا أردنا إضافة متجهين بيانياً، فإن خطوات تطبيق قاعدة أو قانون متوازي الأضلاع هي:

1. أولًا، نرسم المتجهات ونضعها في نفس نقطة التطبيق، أي أننا نضع أصول كلا المتجهين في نفس النقطة.
2. ثم نرسم في نهاية أحد المتجهين خطًا موازيًا للمتجه الآخر. ونكرر الخطوة مع المتجه الآخر. وبالتالي سوف نحصل على رسم متوازي الأضلاع (ومن هنا جاء اسم القاعدة).
3. وأخيرًا، فإن المتجه الناتج عن المجموع سيكون قطر متوازي الأضلاع الذي يمتد من الأصل المشترك للمتجهين إلى نقطة تقاطع الخطين المتوازيين.

في المثال العام التالي، يمكنك رؤية كيفية استخدام قاعدة متوازي الأضلاع:

إذا كنت ترغب في التدرب على قاعدة متوازي الأضلاع، يمكنك في الرابط التالي الاطلاع على المزيد من الأمثلة والعديد من تمارين إضافة المتجهات التي تم حلها . ستجد في هذه الصفحة أيضًا طرقًا أخرى لإضافة المتجهات بيانيًا وحتى كيفية إضافتها رقميًا.

قاعدة متوازي الأضلاع لطرح متجهين

يتم أيضًا استخدام قاعدة أو طريقة متوازي الأضلاع لطرح متجهين من الرسم البياني. لذا فإن خطوات طرح المتجهات هي:

1. أولاً، نمثل المتجهين على الرسم البياني ونضعهما في نفس نقطة التطبيق، أي أننا نضع أصول كلا المتجهين في نفس النقطة.
2. ثانيًا، نرسم المتجه المعاكس للمتجه الذي يتم طرحه في العملية، أو بعبارة أخرى، نعكس المتجه الذي يتم طرحه.
3. ثم نرسم خطًا موازيًا لعلامة تغيير المتجه في نهاية المتجه الذي يضيف ما يصل إلى . ونكرر العملية مع المتجه الآخر. حتى نحصل على رسم متوازي الأضلاع (ومن هنا اسم القاعدة).
4. وأخيرًا، ستكون نتيجة الطرح هي المتجه الذي ينتقل من الأصل المشترك للمتجهين إلى النقطة التي يتقاطع فيها الخطان المتوازيان.

انظر إلى المثال العام التالي الذي يتم فيه طرح متجهين بواسطة قانون متوازي الأضلاع:

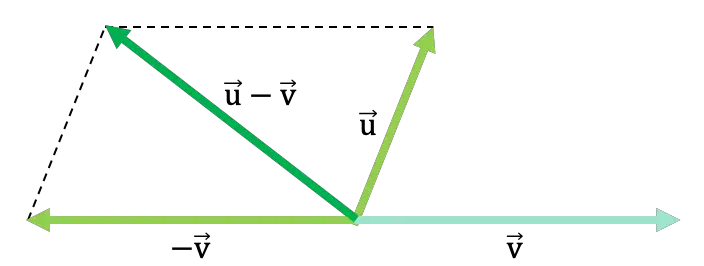
في الرابط التالي، يمكنك رؤية المزيد من الأمثلة على طرح المتجهات باستخدام قاعدة متوازي الأضلاع، ويمكنك أيضًا التدرب على تمارين طرح المتجهات التي تم حلها . بالإضافة إلى ذلك، ستجد تقنيات أخرى لطرح المتجهات من الرسم البياني الخاص بها، وأخيرًا، كيفية طرحها رقميًا.

وأخيرًا، إذا كان شرح هذه التقنية مفيدًا لك، فمن المؤكد أنك ستكون أيضًا مهتمًا بمعرفة ما هي قاعدة اليد اليمنى . في صفحة الارتباط، يمكنك رؤية ماهيتها، وما هي عملية المتجهات التي يتم استخدامها من أجلها، والأشكال المختلفة لهذه القاعدة الموجودة.