الزاوية بين الخط والمستوى

ستجد هنا كيفية حساب الزاوية بين الخط والمستوى. ستتمكن أيضًا من رؤية الأمثلة، بالإضافة إلى التدرب على التمارين التي تم حلها خطوة بخطوة حول الزوايا بين الخطوط والمستويات.

ما هي الزاوية بين الخط والطائرة؟

الزاوية بين الخط والمستوى هي الزاوية بين الخط وإسقاطه المتعامد على المستوى.

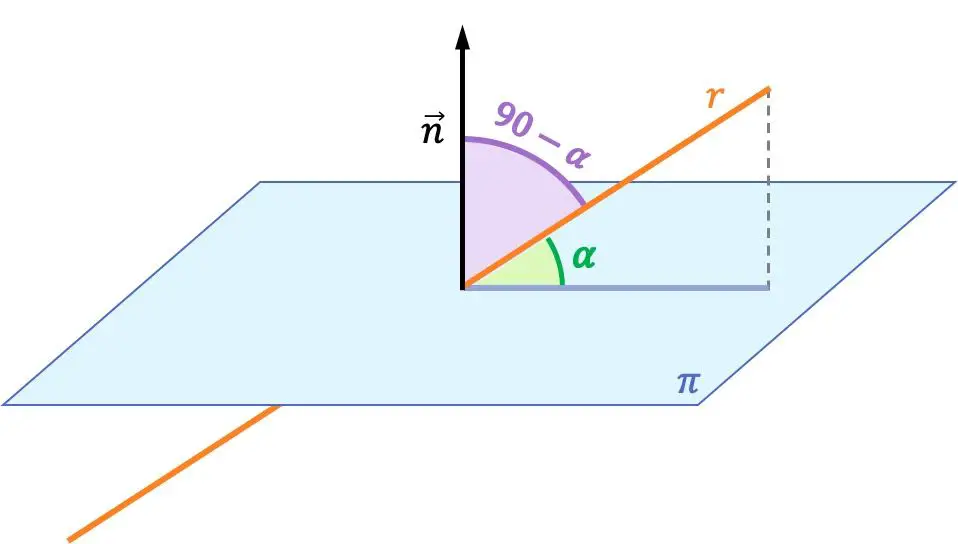
الزاوية بين الخط والمستوى هي تكملة الزاوية بين الخط المذكور والمتجه العمودي للمستوى. لذلك، يتم حساب الزاوية بين الخط والمستوى من الزاوية بين متجه اتجاه الخط والمتجه العمودي للمستوى.

صيغة الزاوية بين الخط والمستوى

لاستنتاج صيغة الزاوية بين المستوى والخط، عليك أن تعرف كيفية العثور على الزاوية بين متجهين . ستجد في الصفحة المرتبطة الشرح بالإضافة إلى الأمثلة والتمارين التي تم حلها خطوة بخطوة، لذا إذا كنت لا تتذكر كيفية القيام بذلك، فنوصيك بإلقاء نظرة.

وبالتالي، بما أن الزاوية بين الخط والمستوى مكملة للزاوية الواقعة بين متجه الاتجاه للخط المذكور

$(\vv{\text{v}}_r)$

والناقل الطبيعي للطائرة المذكورة

$(\vv{n})$

، من صيغة الزاوية بين متجهين نستنتج أن الزاوية بين الخط والمستوى تعادل التعبير التالي:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

وبالتالي فإن صيغة الزاوية بين الخط والمستوى هي :

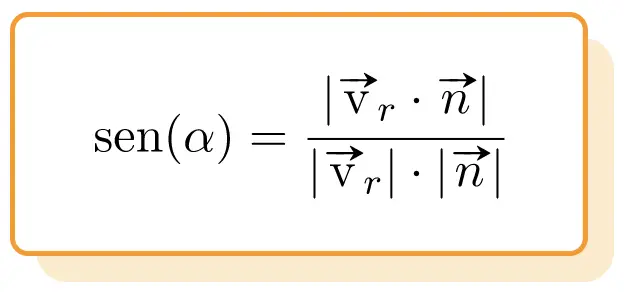
ذهب:

$\vv{\text{v}}_r$

هو المتجه المباشر للخط.
$\vv{n}$

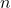
هو المتجه الطبيعي للطائرة.

مثال لحساب الزاوية بين الخط والمستوى

لكي تتمكن من معرفة كيفية حل هذا النوع من المسائل، إليك مثال لحساب الزاوية بين الخط والمستوى:

احسب الزاوية التي يشكلها الخط
$r$

مع الطائرة

$\pi.$

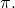
فلتكن معادلاتهم:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

يتم التعبير عن الخط في شكل معادلات بارامترية، بحيث يكون متجه اتجاهه هو:

$\vv{\text{v}}_r = (-1,4,-3)$

من ناحية أخرى، يتم تعريف المستوى في شكل معادلة ضمنية (أو عامة)، لذلك فإن متجهه الطبيعي هو:

$\vv{n} = (1,-1,4)$

وبالتالي، بمجرد أن نعرف متجه الاتجاه للخط والمتجه العمودي للمستوى، فإننا نطبق صيغة الزاوية بين الخط والمستوى:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

نستبدل المتجهات في الصيغة:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

ونقوم بالحسابات:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

وأخيرًا، نعكس جيب الزاوية بالآلة الحاسبة ونوجد قيمة الزاوية:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

وبالتالي فإن الزاوية بين الخط والمستوى تبلغ 51.80 درجة تقريبًا.

يجب أن نأخذ في الاعتبار أننا إذا حصلنا على نتيجة 0°، فهذا يعني أن الخط والمستوى متوازيان أو أن الخط موجود في المستوى. وإذا كانت الزاوية تساوي 90 درجة، فهذا يعني أن الخط والمستوى متعامدان.

حل مسائل الزاوية بين الخط والمستوى

التمرين 1

أوجد الزاوية التي يشكلها الخط

$r$

مع الطائرة

$\pi.$

فلتكن معادلاتهم:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

انظر الحل

يتم التعبير عن الخط كمعادلة مستمرة، وبالتالي فإن متجه اتجاهه هو:

$\vv{\text{v}}_r = (2,-1,-3)$

من ناحية أخرى، يكون المستوى على شكل معادلة ضمنية (أو عامة)، لذا فإن متجهه الطبيعي هو:

$\vv{n} = (3,1,2)$

لذلك، بمجرد أن نعرف متجه الاتجاه للخط والمتجه العمودي للمستوى، نستخدم صيغة الزاوية بين الخط والمستوى:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

وأخيرًا، نعكس الجيب ونوجد قيمة الزاوية:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

وبالتالي فإن الزاوية بين الخط والمستوى هي 4.10 درجة.

تمرين 2

تحديد الزاوية التي يشكلها الخط

$r$

مع الطائرة

$\pi.$

فلتكن معادلاتهم:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

انظر الحل

يتم التعبير عن الخط بمعادلاته الضمنية (أو العامة)، لذلك من الضروري العثور على متجه الاتجاه للخط عن طريق حساب المنتج المتجه للمتجهات العادية للطائرتين اللتين تحددان الخط:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

ومن ناحية أخرى فإن المتجه العمودي للمستوى هو:

$\vv{n} = (-4,2,0)$

لذلك، بمجرد أن نعرف متجه الاتجاه للخط والمتجه العمودي للمستوى، نستخدم صيغة الزاوية بين الخط والمستوى:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

وأخيرًا، نعكس الجيب ونوجد قيمة الزاوية:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

وبالتالي فإن الزاوية بين الخط والمستوى هي 46.33 درجة.

التمرين 3

أوجد، باستخدام صيغة الزاوية بين الخط والمستوى، قيمة

$k$

ضروري للحق

$r$

والطائرة

$\pi$

تكون متوازية.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

انظر الحل

أولاً، يتم التعبير عن الخط كمعادلة متجهة، لذا فإن متجه اتجاهه هو:

$\vv{\text{v}}_r = (4,-1,3)$

ومن ناحية أخرى، يكون المستوى على شكل معادلة عامة، لذا فإن متجهه الطبيعي هو:

$\vv{n} = (4,3,k)$

إذن، لكي يكون العنصران الهندسيان متوازيين، يجب أن تكون الزاوية بينهما صفرًا. وبالتالي فإن صيغة الزاوية بين الخط والمستوى هي:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

ومن ثم، يجب أن يكون حاصل الضرب النقطي بين متجه الاتجاه للخط والمتجه العادي صفرًا. ومن هذه المعادلة يمكننا تحديد قيمة المجهول

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

أخيرًا، إذا وجدت هذه المقالة مفيدة، فمن المحتمل أنك مهتم أيضًا بكيفية العثور على الزاوية بين طائرتين . ستجد في صفحة الروابط شرحًا مفصلًا للغاية بالإضافة إلى الصيغة اللازمة لحساب الزاوية بين مستويين مختلفين، بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة لتتمكن من التدريب والفهم كيف يتم ذلك على أكمل وجه.

ما هي الزاوية بين الخط والطائرة؟

صيغة الزاوية بين الخط والمستوى

مثال لحساب الزاوية بين الخط والمستوى

حل مسائل الزاوية بين الخط والمستوى

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد