التحولات الوظيفية: الترجمة والتوسع والتماثل

تشرح هذه الصفحة ماهية تحويلات الوظائف وكيفية العثور عليها. هناك ثلاثة أنواع من التحولات: الترجمات (أو الإزاحات)، والتماثلات والتوسعات (أو الانكماشات). ستجد أيضًا تمارين تم حلها خطوة بخطوة حتى تتمكن من التدرب على المفاهيم وفهمها دون ترك أي شك.

ما هي التحولات الوظيفية؟

في بعض الأحيان قد يُطلب منا رسم بياني لدوال أولية تشبه إلى حد كبير وظائف أخرى نعرفها بالفعل. حسنًا، بدلًا من تمثيل دالة مماثلة مرة أخرى، يمكن استخدام التقنيات للتبديل من تمثيل دالة إلى أخرى بسهولة وسرعة.

وبالتالي، فإن تحويلات الوظائف هي تقنيات تجعل من الممكن الانتقال من التمثيل الرسومي لدالة إلى التمثيل الرسومي لوظيفة أخرى مشابهة جدًا من خلال العمليات الأولية.

في الأساس، هناك ثلاثة أنواع من تحويلات الوظائف الأولية:

الترجمات أو الحركات : يمكن تحريك الوظيفة رأسيًا وأفقيًا.
الانعكاسات أو التماثلات : يمكن أن تنعكس الدالة باستخدام المحور X أو المحور Y كمحور تماثل.
التوسعات والضغطات : يمكن تكبير الوظيفة أو تصغيرها.

بمجرد أن نرى مفهوم تحويل دالة، سوف نتعمق في كل نوع من أنواع التعديل.

ترجمات أو حركات الوظائف

سنبدأ بالتحولات الوظيفية. هناك نوعان: الترجمات الرأسية والترجمات الأفقية.

الترجمة أو الحركة العمودية للدالة

لترجمة دالة أو نقلها عموديًا (على طول المحور Y)، يجب عليك إضافة أو طرح ثابت للدالة:

نقوم بنقل وحدات الدالة k إلى الأعلى بإضافة ka إلى الدالة:

$\bm{f(x)+k}$

نقوم بنقل الدالة k من الوحدات إلى الأسفل عن طريق طرح ka من الدالة:

$\bm{f(x)-k}$

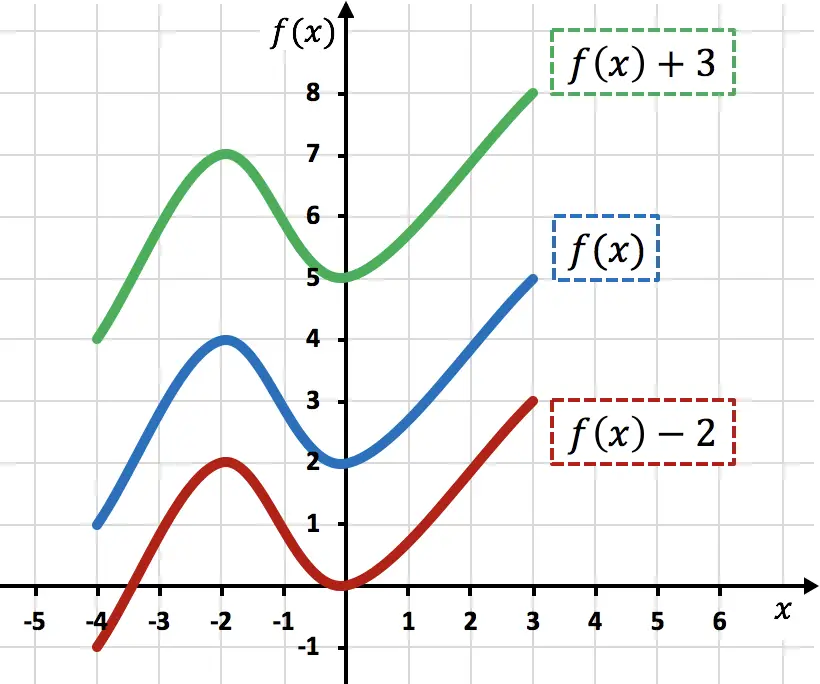
كما ترون من الرسم البياني، فإن إضافة ثابت إلى أي دالة يؤدي إلى تغيير الوحدات المضافة لأعلى (الدالة الخضراء). من ناحية أخرى، عند طرح رقم من دالة، يتم نقل الوحدات المطروحة للأسفل (الدالة الحمراء).

لاحظ أنه في هذا النوع من الحركات يتم تغيير إحداثيات Y فقط لنقاط الوظيفة، بينما تظل إحداثيات X كما هي.

الترجمة أو الحركة الأفقية للوظائف

لترجمة دالة أو تحويلها أفقيًا (على طول المحور X)، يجب عليك إضافة أو طرح ثابت إلى المتغير المستقل x :

الرسم البياني ل

$\bm{f(x+k)}$

هو الرسم البياني ل

$f(x)$

انتقلت وحدات k إلى اليسار.

الرسم البياني ل

$\bm{f(x-k)}$

هو الرسم البياني ل

$f(x)$

تحولت وحدات k إلى اليمين.

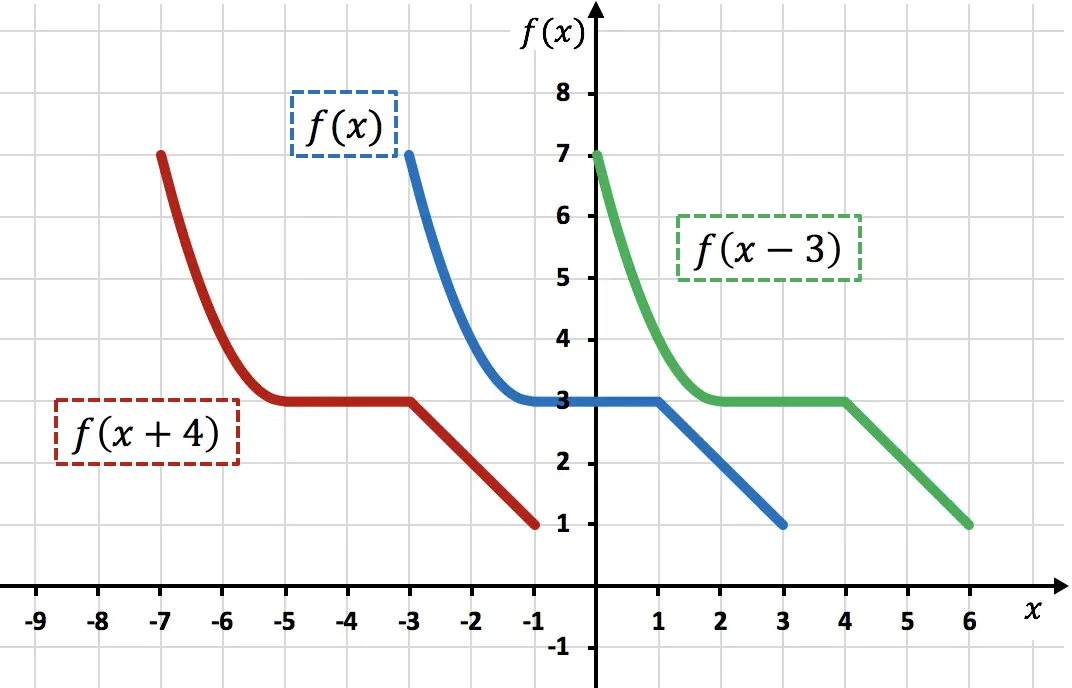
كما ترون من الرسم البياني، عند إضافة ثابت مباشرة إلى المتغير x ، تقوم الدالة بإزاحة الوحدات المضافة إلى اليسار (الدالة الحمراء). من ناحية أخرى، عند طرح رقم من المتغير x ، تقوم الدالة بإزاحة الوحدات المطروحة إلى اليمين (الدالة الخضراء).

لاحظ أنه في هذا النوع من الحركات، يتم تغيير إحداثيات X فقط لنقاط الوظيفة، بينما تستمر إحداثيات Y بنفس القيمة.

مثال على ترجمة أو نقل وظيفة

انقل الدالة التالية 4 وحدات لأعلى و 3 وحدات إلى اليمين:

$f(x)=x^2$

لنقل الدالة لأعلى بمقدار 4 وحدات، نحتاج إلى إضافة 4 وحدات إلى الدالة:

$f(x) + 4 = x^2 + 4$

ولتحريك الدالة أيضًا بمقدار 3 وحدات إلى اليمين، يجب علينا الحساب

$f(x-3)$

. لذلك، حيث يوجد

$x$

في وسعنا

$x-3 :$

$f(x-3) = (x-3)^2 + 4$

الدالة التي تم إزاحتها بمقدار 4 وحدات لأعلى و3 وحدات إلى اليمين هي:

$\bm{f(x) = (x-3)^2 + 4}$

يوجد أدناه الوظيفة الأصلية والوظيفة المحولة رسومًا بيانية حتى تتمكن من رؤية الفرق بينهما:

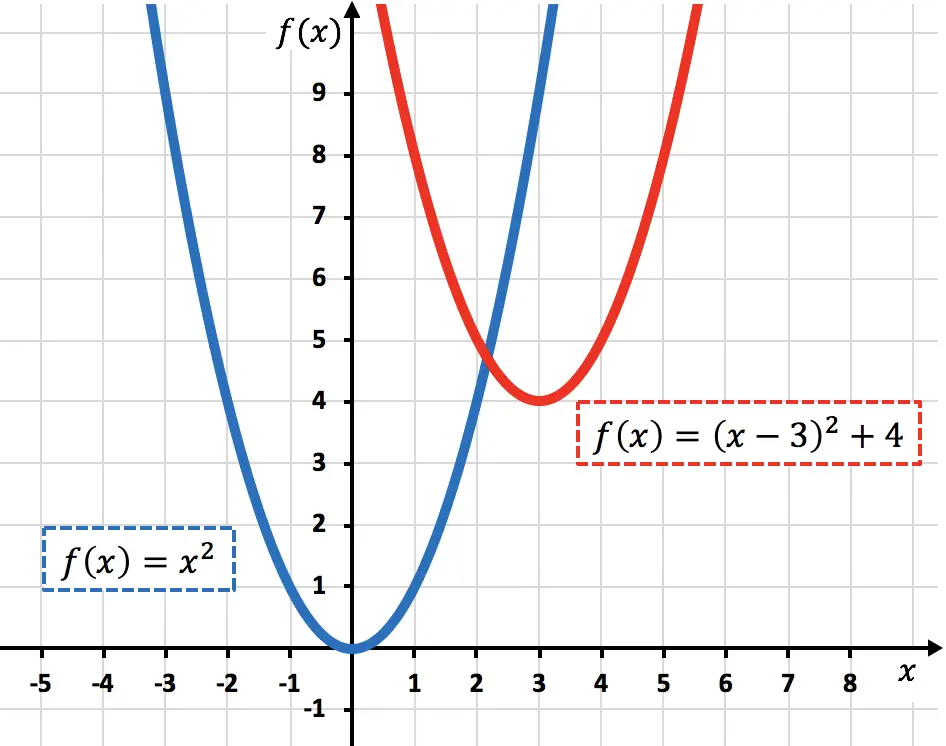
يسمي بعض علماء الرياضيات الإزاحة المائلة أو الانتقال عندما يحدث كلا النوعين من الحركة في نفس الوقت.

انعكاس أو تناظر الدالة بالنسبة إلى محاور الإحداثيات

يمكننا تمثيل الدالة المتماثلة بالنسبة لأي محور ديكارتي بالطريقة التالية:

لعكس دالة بالنسبة إلى المحور السيني، نحتاج إلى تغيير إشارة الدالة، أي أننا نحتاج إلى الحساب

$\bm{-f(x)}.$

لعكس دالة بالنسبة للمحور y، يجب علينا إلغاء المتغير المستقل x ، أي أنه يجب علينا الحساب

$\bm{f(-x)}.$

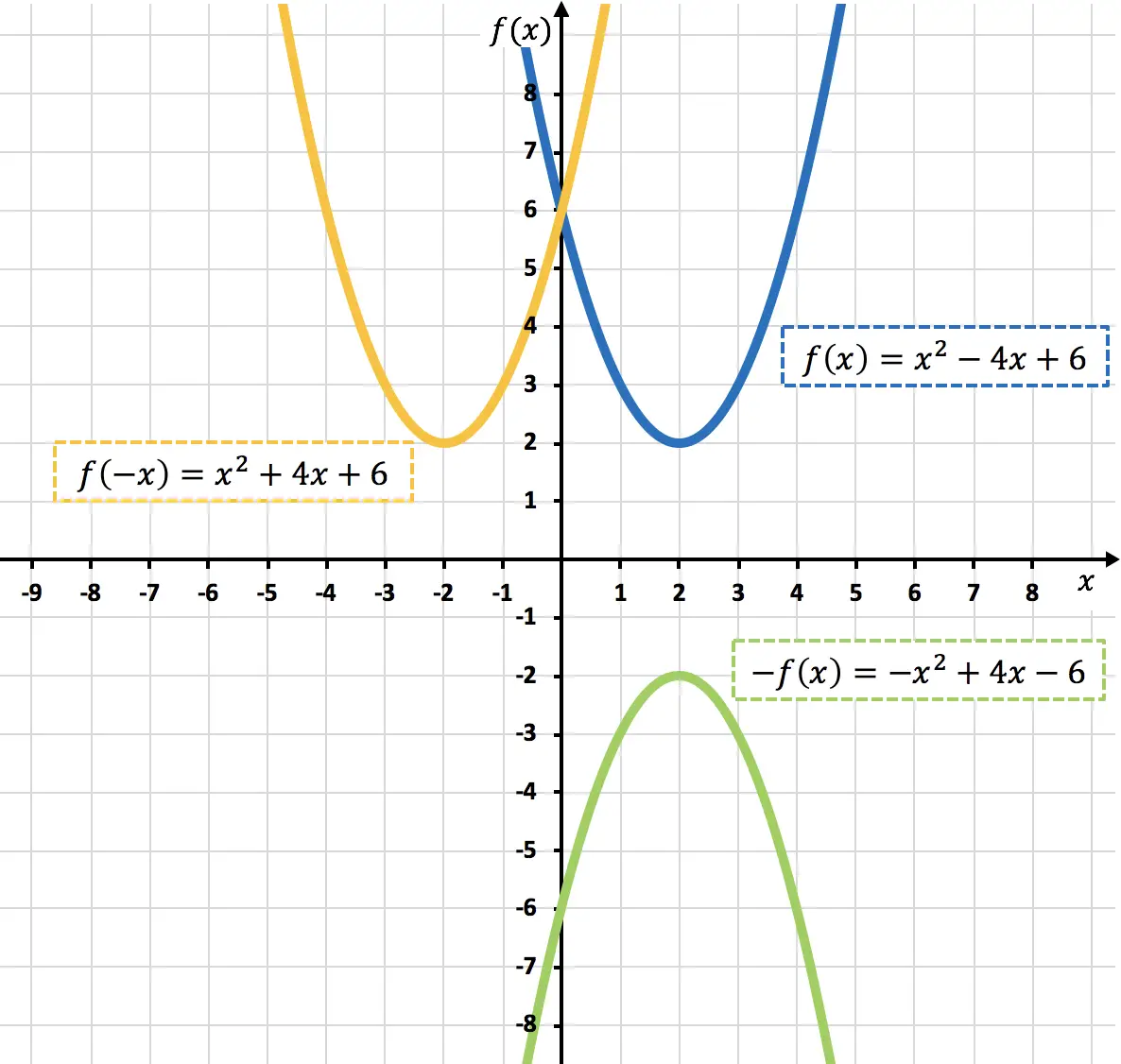
كما ترون في الرسم البياني السابق، من خلال ضرب الدالة في -1، فإننا نعكسها بيانيًا (الدالة البرتقالية)، أو بعبارة أخرى، نعكسها بالنسبة إلى المحور X.

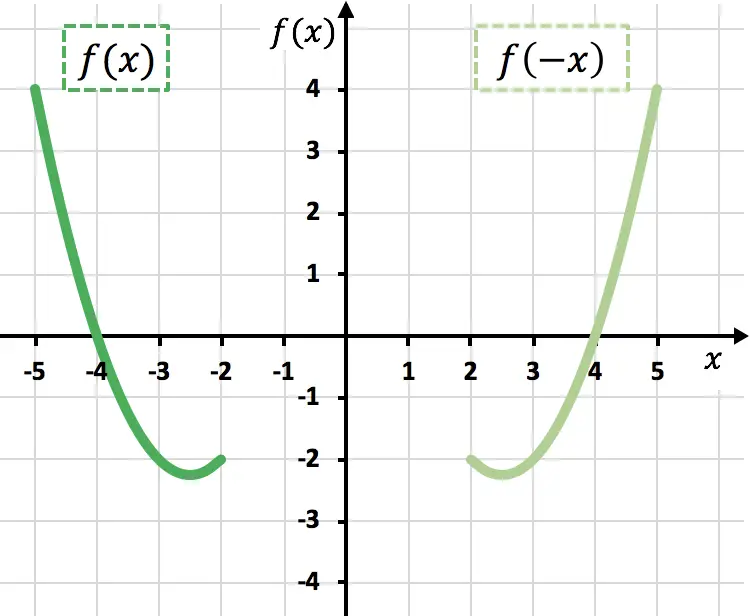
كما هو واضح في الرسم البياني السابق، من خلال إلغاء المتغير x ، فإننا نعكس الدالة بالنسبة إلى المحور Y (الدالة الخضراء الفاتحة).

مثال على عكس وظيفة

احسب الدالة المتماثلة حول محور OX والدالة المتماثلة حول محور OY للدالة التربيعية التالية:

$f(x)=x^2-4x+6$

للعثور على الدالة المتناظرة بالنسبة إلى المحور X، علينا أن نفعل ذلك

$-f(x)$

$-f(x)=-\bigl[x^2-4x+6\bigr]$

$\bm{-f(x)=-x^2+4x-6}$

ولإيجاد الدالة المتناظرة بالنسبة للمحور Y يجب علينا القيام بذلك

$f(-x)$

. لذلك، نستبدل حيث يوجد

$x$

في الوظيفة الأصلية حسب المصطلح

$-x :$

$f(x)=x^2-4x+6$

$f(-x)=(-x)^2-4\cdot (-x)+6$

$f(-x)=x^2-4\cdot (-x)+6$

$\bm{f(-x)=x^2+4x+6}$

لقد قمت أدناه بتمثيل كل من الوظيفة الأصلية والوظائف المتماثلة الموجودة:

مثال على الدوال المتناظرة حول المحورين x وy

التوسعات الوظيفية والتقلصات

كما هو الحال مع الترجمات، هناك نوعان من التوسعات أو التقلصات: الرأسي والأفقي.

التوسع الرأسي والانكماش للدالة

من خلال ضرب دالة عددية في معامل، يمكننا جعلها تتوسع أو تنكمش:

لتوسيع (أو توسيع) دالة على المحور Y، نحتاج إلى ضربها برقم أكبر من 1:

$kf(x)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> <p style=$ لتصغير دالة على المحور Y، نحتاج إلى ضربها برقم موجب أقل من 1:

$kf(x)\qquad 0</div> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="http://mathority.org/wp-content/uploads/2023/07/expansion-et-contraction-d-une-fonction.webp" alt="expansion et contraction verticales d'une fonction" class="wp-image-320" width="442" height="438" srcset="" sizes="" data-src=""></figure> </div> <p> Comme vous pouvez le voir dans le graphique précédent, si on multiplie une fonction par un coefficient supérieur à 1 (fonction verte) on la rend plus grande le long de l’axe OY, en revanche, si on multiplie une fonction par un coefficient supérieur à 0 mais plus petit que 1 (fonction rouge), nous le rendons plus petit le long de l’axe OY.</p> <h3 class="wp-block-heading"> Expansion et contraction horizontales d’une fonction</h3> <p> Dans ce cas, au lieu de multiplier la fonction entière par un coefficient, pour qu’une fonction se dilate ou se contracte horizontalement, nous devons multiplier la variable indépendante <em>x</em> . </p> <div style="padding-top: 23px; padding-bottom: 0.5px; padding-right: 30px; padding-left: 30px; border: 2px dashed #FF9B28; border-radius:20px;"> Pour <strong>étendre (ou dilater) une fonction sur l’axe X,</strong> il faut multiplier tous les <em>x</em> par un nombre compris entre 0 et 1 :” title=”Rendered by QuickLaTeX.com” height=”392″ width=”2425″ style=”vertical-align: -4px;”></p> <p> و(ك س)\كربع 0</p> <p style=$ لتصغير دالة على المحور X، نحتاج إلى ضرب جميع قيم x برقم أكبر من 1:

$f(kx)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> </div> <div class=$

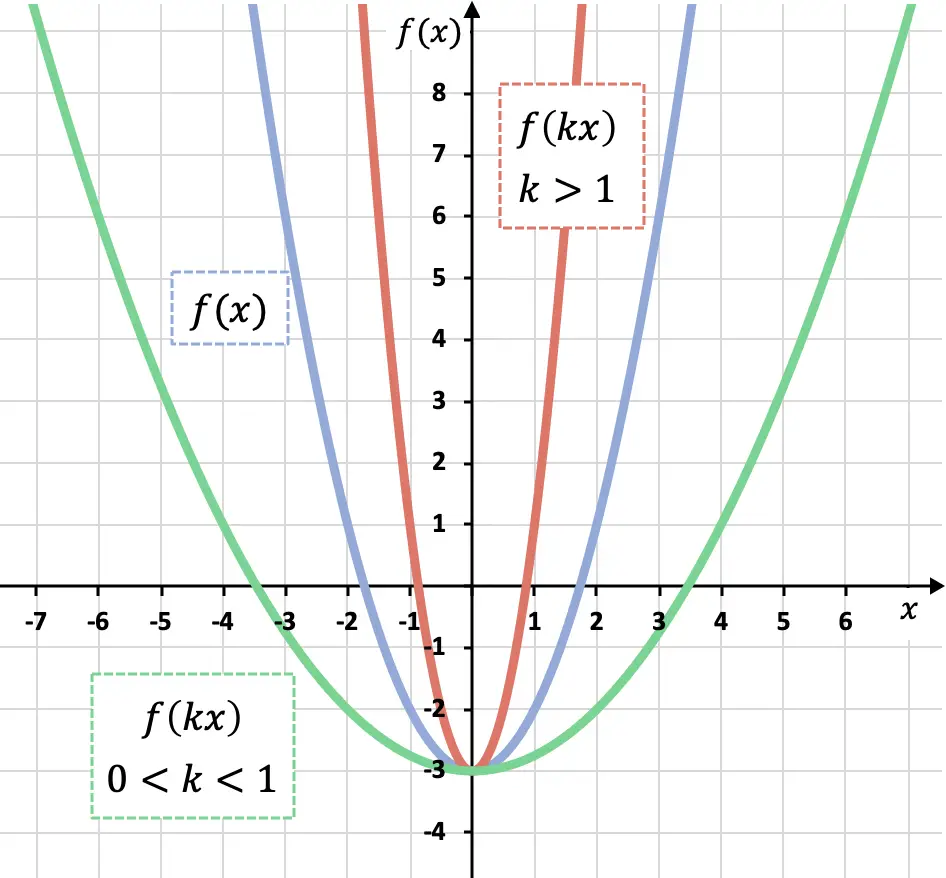
كما ترون في الرسم البياني السابق، إذا ضربنا جميع قيم x للدالة في معامل أكبر من 0 ولكن أقل من 1 (دالة خضراء) فإننا نقوم بتكبيرها على طول محور OX، ومن ناحية أخرى، إذا ضربنا دالة بمعامل أكبر من 1 (دالة حمراء) نقوم بتقليلها على طول محور OX.

مثال لكيفية توسيع دالة أو طيها

قم بتكرار الدالة غير المنطقية التالية رأسيًا وأفقيًا:

$f(x)=\sqrt{9-x^2}$

لتمديد الدالة على المحور y بمقدار اثنين، يجب علينا ضرب الدالة بأكملها في 2:

$2f(x)=2\sqrt{9-x^2}$

ولتوسيع الدالة أيضًا بمقدار اثنين على المحور السيني، يجب علينا ضرب جميع قيم x للدالة في

$\displaystyle \frac{1}{2}:$

$\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}$

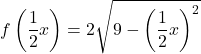
وبالتالي فإن الوظيفة المكررة على محوري الإحداثيات هي:

$\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}$

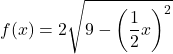
يوجد أدناه الوظيفة الأصلية والوظيفة المحولة ممثلة بيانيًا حتى تتمكن من رؤية الاختلافات بينهما:

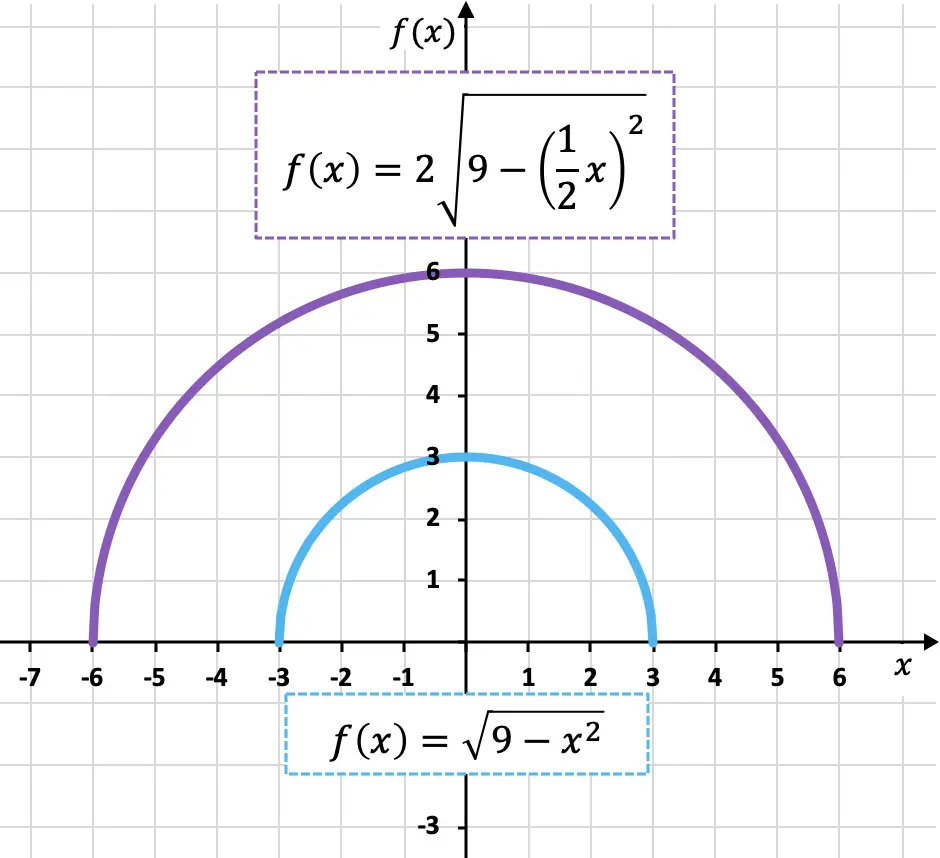
كما ترون، فإن الميزة الجديدة (اللون الأرجواني) أكبر بمرتين من الميزة الأصلية (اللون الأزرق) رأسيًا وأفقيًا، وبالتالي تم توسيع الميزة.

تمارين محلولة على تحويلات الدالة

التمرين 1

انقل دالة الدرجة الثالثة التالية إلى أعلى بمقدار 5 وحدات:

$f(x) = 4x^3-9x-2$

انظر الحل

لتحريك الدالة لأعلى بمقدار 5 وحدات، أضف 5 إلى الدالة:

$\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}$

وبالتالي فإن الدالة التي تم إزاحتها بمقدار 5 وحدات هي:

$\bm{f(x) = 4x^3-9x+3}$

تمرين 2

أوجد الدالة المتماثلة حول المحور Y للدالة التربيعية التالية:

$f(x) = 2x^2-3x+6$

انظر الحل

للعثور على الدالة المتناظرة بالنسبة للمحور Y، من الضروري إجراء الحساب

$f(-x)$

أي أننا بحاجة إلى الاستبدال

$x$

$-x$

في الدالة:

$f(-x) = 2(-x)^2-3\cdot (-x)+6$

$f(-x) = 2x^2+3x+6$

وبالتالي فإن الدالة المتماثلة بالنسبة لمحور OY هي:

$\bm{f(x) = 2x^2+3x+6}$

التمرين 3

قم بإجراء ضغط أفقي للدالة التالية إلى ثلث تمثيلها:

$f(x) = x^3-4x^2-5x+1$

انظر الحل

لتقليل وظيفة من خلال

$f(3x) = (3x)^3-4(3x)^2-5(3x)+1$

$f(3x) = 27x^3-4\cdot 9 x^2-15x+1$

$f(3x) = 27x^3-36 x^2-15x+1$

وبالتالي فإن الوظيفة المخفضة هي:

$\bm{f(x) = 27x^3-36 x^2-15x+1}$

التمرين 4

احسب الدالة المتناظرة بالنسبة لمحور OX للدالة التالية المترجمة 4 وحدات إلى اليمين:

$f(x) = 3x^3-x^2+5x+8$

انظر الحل

قبل حساب الدالة المتماثلة، يجب علينا أولاً تحريك الدالة 4 وحدات إلى اليمين، وبالتالي:

$f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-12$

وبمجرد تحريك الدالة، نحسب الدالة المتماثلة بالنسبة إلى المحور X. للقيام بذلك، يجب علينا إلغاء الوظيفة التي تم الحصول عليها:

$\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]$

$-f(x) = -3(x-4)^3+(x-4)^2-5x+12$

وباختصار، فإن الوظيفة بعد تطبيق جميع العمليات الأولية هي:

$\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}$

التمرين 5

انقل الدالة التالية وحدتين إلى اليسار، ثم قم بتوسيعها رأسيًا بعامل 4:

$f(x) = x^4-5x^3-x-3$

انظر الحل

أولاً، نقوم بتحريك الدالة وحدتين إلى اليسار:

$f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-2-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-5$

ثم نقوم بتوسيع الدالة على طول المحور Y بعامل 4:

$4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]$

$f(x) = 4(x+2)^4-20(x+2)^3-4x-20$

في الختام، فإن الدالة بعد تطبيق جميع التحويلات الأولية هي:

$\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}$

التمرين 6

من الوظيفة

$f(x)=x,$

تحديد أي من التمثيلات على الرسم البياني يتوافق مع الوظيفة

$f(x)=x-3 .$

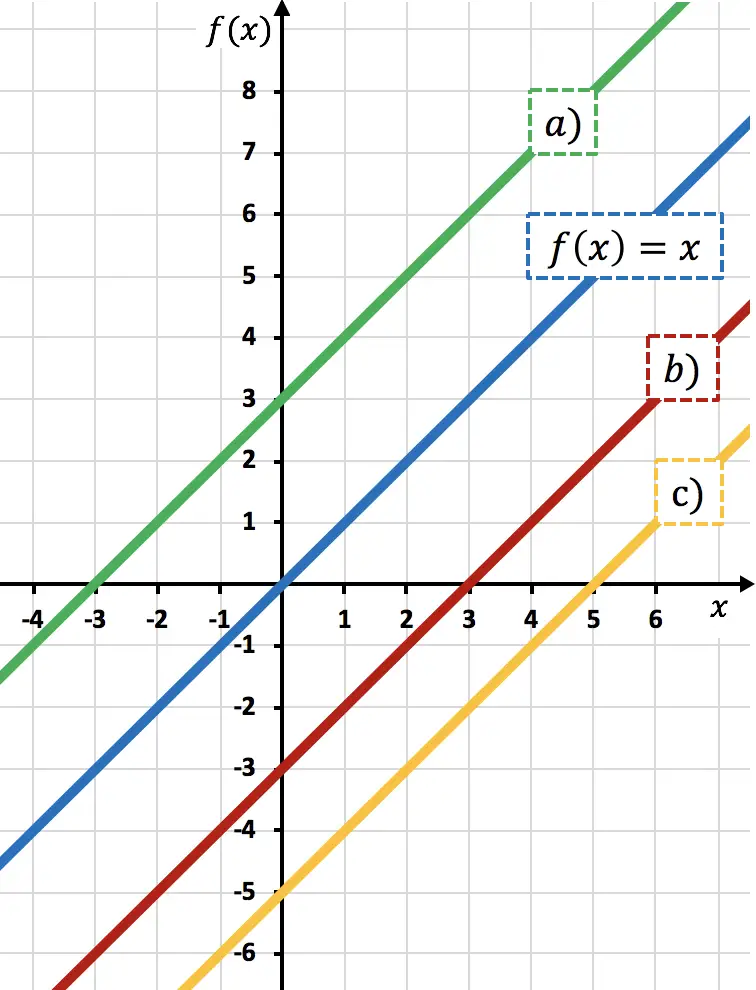
تمارين تم حلها خطوة بخطوة حول تحويلات الدالة

انظر الحل

وظيفة

$f(x)=x-3$

هي الوظيفة

$f(x)=x$

تحركت 3 وحدات إلى أسفل. لأنه بطرح رقم من دالة، فإنك تنقل الدالة إلى الأسفل.

ولذلك فإن تمثيل

$f(x)=x-3$

يتوافق مع الخط ب) لأنه تم إزاحته بمقدار 3 وحدات للأسفل مقارنة بـ

$f(x)=x .$

ويمكن ملاحظة ذلك من خلال النظر إلى المحور الرأسي: متى

$f(x)=x$

يمر عبر 0، والخط الأحمر يمر عبر -3، لذلك يتم إزاحته بمقدار 3 وحدات لأسفل.

التمرين 7

من الوظيفة

$f(x)=x^2+2,$

تحديد القطع المكافئ الذي يمثل الدالة

$f(x)=(x-6)^2+2 .$

انظر الحل

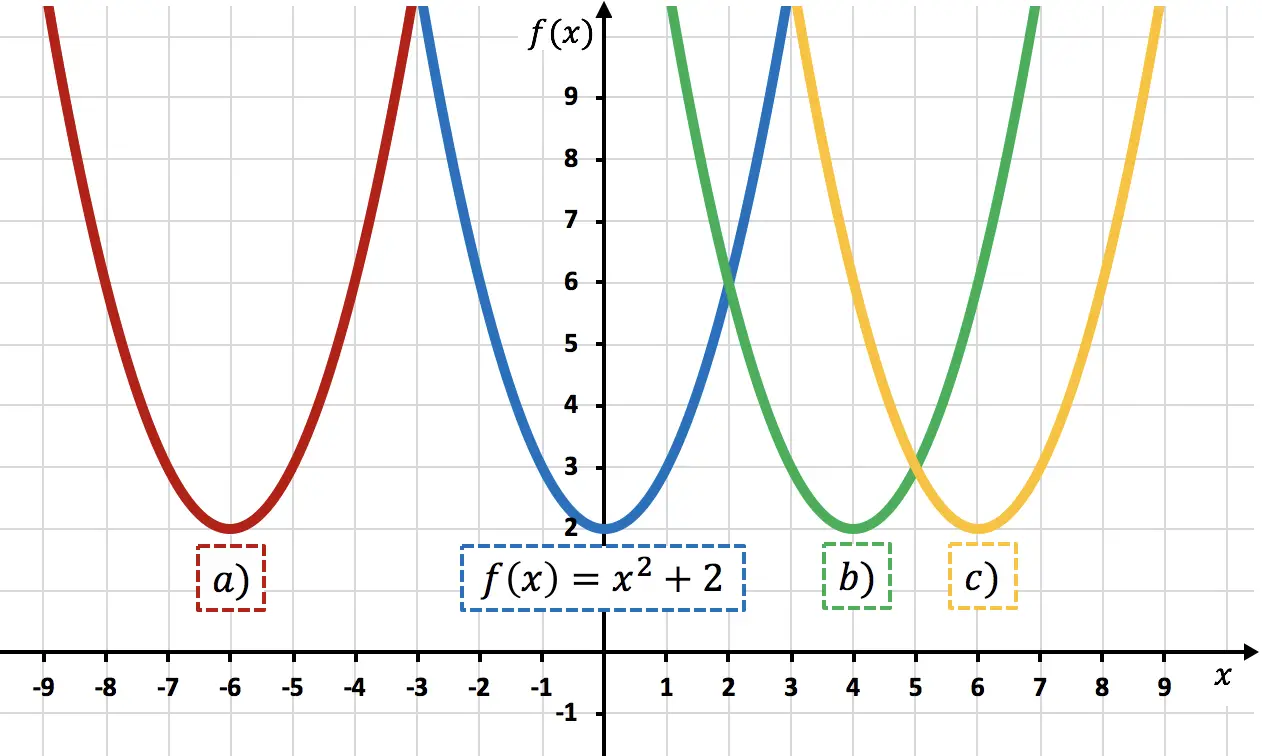
وظيفة

$f(x)=(x-6)^2+2$

هي الوظيفة

$f(x)=x^2+2$

تحركت 6 وحدات إلى اليمين. يمكننا التحقق من ذلك عن طريق الحساب

$f(x-6):$

$f(x)=x^2+2$

$f(x-6)=(x-6)^2+2$

ولذلك فإن تمثيل

$f(x)=(x-6)^2+2$

يتوافق مع القطع المكافئ ج) لأنه تم إزاحته بمقدار 6 وحدات إلى اليمين مقارنة بـ

$f(x)=x^2+2$

ويمكن ملاحظة ذلك من خلال النظر إلى رؤوس القطع المكافئة: المسافة بين رؤوس القطع المكافئ

$f(x)=x^2+2$

ورأس القطع المكافئ ج) يساوي 6 وحدات، وبالتالي يتم إزاحة الأخير بمقدار 6 وحدات إلى اليمين مقارنة بالأول.

تحويلات الدالة: الترجمات، التماثل، التوسيع والضغط

ما هي التحولات الوظيفية؟

ترجمات أو حركات الوظائف

الترجمة أو الحركة العمودية للدالة

الترجمة أو الحركة الأفقية للوظائف

مثال على ترجمة أو نقل وظيفة

انعكاس أو تناظر الدالة بالنسبة إلى محاور الإحداثيات

مثال على عكس وظيفة

التوسعات الوظيفية والتقلصات

التوسع الرأسي والانكماش للدالة

مثال لكيفية توسيع دالة أو طيها

تمارين محلولة على تحويلات الدالة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

اترك تعليقاً إلغاء الرد