▷ كيف أعرف إذا كانت 3 نقاط (أو أكثر) محاذية؟ ✅

ستجد في هذه الصفحة شرحًا لماهية النقاط المحاذية. سترى أيضًا جميع الطرق المتاحة لتحديد ما إذا كانت 3 نقاط (أو أكثر) محاذية أم لا. والأكثر من ذلك، ستجد العديد من الأمثلة وحتى التمارين المحلولة حتى تتمكن من التدرب.

ماذا يعني أن النقاط متوازية؟

في الهندسة التحليلية، تتم محاذاة ثلاث نقاط أو أكثر إذا كانت جميعها على نفس الخط، أي إذا كان من الممكن ضمها عن طريق رسم خط مستقيم بينها.

من الواضح أن النقطتين ستتم محاذاةهما دائمًا، حيث يمكنك دائمًا رسم خط بين نقطتين. ومع ذلك، لا يجب أن تكون النقاط الثلاث على نفس الخط. بشكل أساسي، هناك طريقتان لمعرفة ما إذا كانت 3 نقاط أو أكثر محاذية:

طريقة المتجهات : تتكون من معرفة ما إذا كانت المتجهات التي تشكل النقاط متناسبة.
طريقة المعادلة الخطية : تتمثل في تحديد ما إذا كانت النقاط تنتمي إلى نفس الخط.

فيما يلي شرح لكل إجراء وأمثلة حتى تتمكن من تحديد الإجراء الأفضل بالنسبة لك.

كيفية معرفة ما إذا كانت 3 نقاط (أو أكثر) تتماشى مع طريقة المتجه

بالنظر إلى ثلاث نقاط:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

تتم محاذاة النقاط الثلاث إذا كانت المتجهات

$\vv{AB}$

$\vv{BC}$

لهما نفس الاتجاه، أي إذا كانت مركباتهما متناسبة.

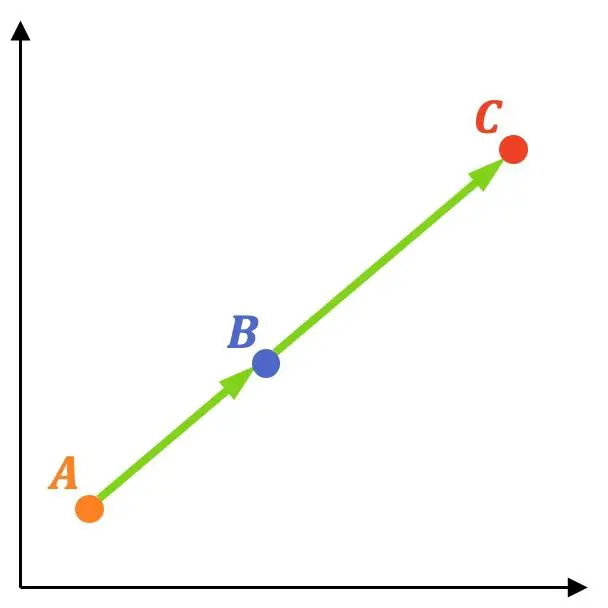
دعونا نرى مثالاً لكيفية القيام بذلك:

حدد ما إذا كانت النقاط الثلاث التالية متوافقة:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

أولا، نحسب المتجهات بين النقاط. يكفي حساب متجهين مختلفين:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

ثم نتحقق مما إذا كانت إحداثيات المتجهات متناسبة:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

بقسمة مكونات X ومركبات Y للمتجهين نحصل على نفس النتيجة (-2)، وبالتالي فإن المتجهات لها نفس الاتجاه، وبالتالي تتم محاذاة النقاط .

يمكن أيضًا استخدام هذه الطريقة لمعرفة ما إذا كانت هناك ثلاث نقاط أو أكثر محاذية في الفضاء (في R3)، والشيء الوحيد الذي يجب إضافته هو التحقق من أن المكون الثالث للمتجهين (المكون Z) متناسب أيضًا.

إذا كانت هذه المقالة مفيدة لك، فمن المحتمل أيضًا أن تكون مهتمًا بمعرفة كيفية حساب نقطة المنتصف بين نقطتين ، لأنه من الواضح أن العثور على نقطة المنتصف لنقطتين هو وسيلة لتحديد نقطة ثالثة تتماشى مع النقطتين الأخريين. يمكنك أن ترى كيف يتم ذلك على الصفحة المرتبطة، بالإضافة إلى أنك ستتمكن أيضًا من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

كيفية معرفة ما إذا كانت 3 نقاط (أو أكثر) تتماشى مع طريقة معادلة الخط المستقيم

كما رأينا في القسم السابق، إحدى الطرق لدراسة محاذاة 3 نقاط أو أكثر هي استخدام المتجهات التي يمكن أن تتشكل بينها. حسنًا، هناك طريقة أخرى وهي البدء بمعادلة الخط:

بالنظر إلى ثلاث نقاط:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

تتم محاذاة النقاط الثلاث إذا كانت جميعها تنتمي إلى نفس الخط. ولذلك، لمعرفة ما إذا كانت هناك ثلاث نقاط أو أكثر محاذية، يجب اتباع الخطوات التالية:

أوجد معادلة الخط المستقيم الذي يمر بنقطتين من النقاط الثلاث.
تحقق مما إذا كانت النقطة الثالثة تنتمي أيضًا إلى السطر. في هذه الحالة يعني ذلك أن النقاط الثلاث متوازية، ولكن إذا لم يتم استيفاء الشرط فهذا يعني أن النقاط غير متوازية.

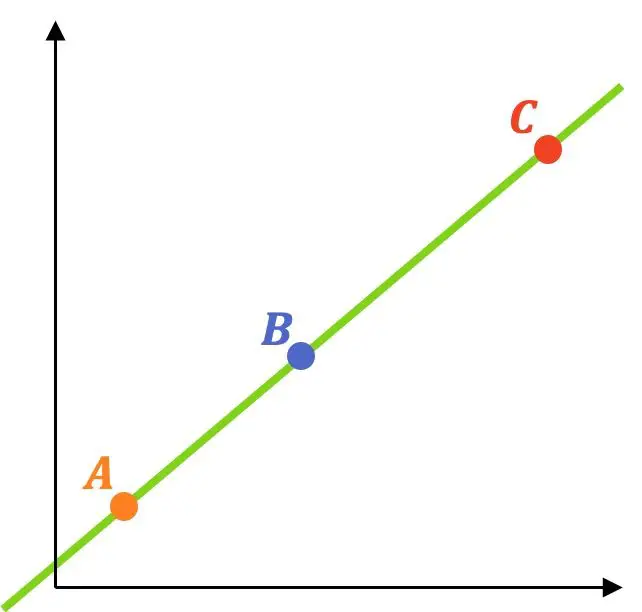
على سبيل المثال، سوف نقوم بحل تمرين باستخدام هذه الطريقة:

تأكد من محاذاة النقاط الثلاث التالية:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

أولًا، يجب علينا حساب معادلة الخط الذي يمر بالنقطتين A وB. وبالتالي، نجد متجه الاتجاه للخط:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

الآن عليك إنشاء معادلة الخط، يمكنك اختيار النوع الذي تريده: بارامترية، ضمنية، عامة، إلخ. لكن في هذه الحالة سوف نستخدم المعادلة المستمرة. وبالتالي فإن المعادلة المستمرة للخط المستقيم الذي يمر بالنقطة A والنقطة B ستكون:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

بمجرد أن نحصل على معادلة الخط، يجب علينا التحقق مما إذا كانت النقطة الأخرى تنتمي أيضًا إلى نفس الخط. للقيام بذلك، نعوض بإحداثيات النقطة C في معادلة الخط:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

لقد حصلنا على التعادل، وبالتالي فإن النقطة تحقق معادلة الخط. وبالتالي فإن النقاط الثلاث تقع على خط واحد .

تجدر الإشارة إلى أن مجموعة النقاط المحاذية لا يجب أن تكون متساوية البعد، أي أن المسافة بين عدة نقاط محاذية قد تكون مختلفة. يمكنك مشاهدة الفرق بين المفهومين في شرح المسافة بين نقطتين (الهندسة) حيث يمكنك أيضا مشاهدة أمثلة وتمارين محلولة خطوة بخطوة.

حل تمارين النقاط المحاذاة

التمرين 1

حدد ما إذا كانت النقاط الثلاث التالية متوافقة:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

انظر الحل

يمكننا اختيار إحدى الطريقتين اللتين رأيناهما لحل المشكلة. في هذه الحالة سوف نستخدم طريقة المتجهات.

أولاً نحسب المتجهات بين النقاط:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

والآن نتحقق مما إذا كانت الإحداثيات الديكارتية للمتجهات متناسبة:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

وبتقسيم مكونات X ومركبات Y للمتجهين على بعضهما البعض نحصل على نفس النتيجة (-4)، وبالتالي فإن المتجهات لها نفس الاتجاه. الحقيقة التي تشير إلى محاذاة النقاط .