قاعدة كريمر – الماتوريتي

ستشاهد في هذه الصفحة ما هي قاعدة كرامر، بالإضافة إلى ذلك، ستجد أمثلة وتمارين لحل أنظمة المعادلات من خلال قاعدة كرامر.

ما هي قاعدة كريمر؟

قاعدة كرامر هي طريقة تستخدم لحل أنظمة المعادلات بواسطة المحددات. دعونا نرى كيف يتم استخدامه:

النظر في نظام المعادلات:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

المصفوفة A والمصفوفة الموسعة A’ للنظام هما:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

تنص قاعدة كريمر على أن حل نظام المعادلات هو:

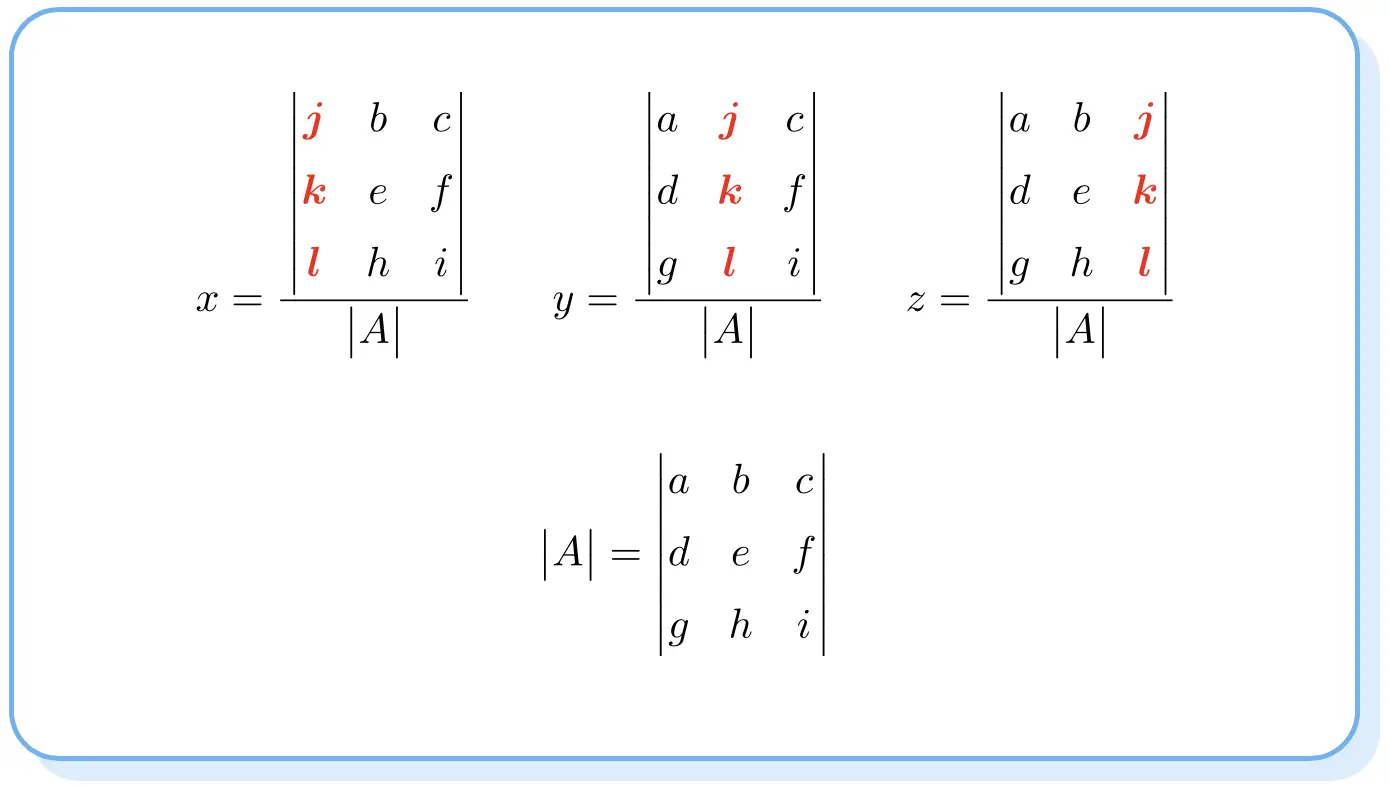
لاحظ أن محددات البسطين تشبه محددات المصفوفة A ولكن يتم تغيير عمود كل مجهول إلى عمود الحدود المستقلة.

ولذلك، يتم استخدام قاعدة كرامر لحل أنظمة المعادلات الخطية. ولكن، كما تعلمون، هناك العديد من الطرق لحل نظام المعادلات، على سبيل المثال طريقة غاوس جوردان معروفة جيداً.

فيما يلي أمثلة لحل أنظمة المعادلات الخطية باستخدام قاعدة كرامر، أو أحيانًا تُكتب أيضًا على هيئة قاعدة كرامر.

مثال 1: تحديد النظام المتوافق (SCD)

حل النظام التالي المكون من 3 معادلات ذات 3 مجاهيل باستخدام قاعدة كرامر:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

نقوم الآن بحساب رتبة المصفوفتين لمعرفة نوع النظام. لحساب رتبة A، نحسب المحدد 3×3 للمصفوفة بأكملها (باستخدام قاعدة ساروس) ونرى ما إذا كانت تعطي 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

محدد A يختلف عن 0، لذا فإن المصفوفة A لها الرتبة 3.

$\displaystyle rg(A)=3$

لذا فإن المصفوفة A’ هي أيضًا من الرتبة 3 ، حيث لا يمكن أن تكون من الرتبة 4 ويجب أن تكون على الأقل من نفس رتبة المصفوفة A.

$\displaystyle rg(A')=3$

مدى المصفوفة A يساوي مدى المصفوفة A’ وعدد المجهولات للنظام (3)، وبالتالي، من خلال نظرية روشيه-فروبينيوس ، نعلم أنه نظام متوافق محدد (SCD):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

بمجرد أن نعرف أن النظام هو SCD، نطبق قاعدة كرامر لحلها. للقيام بذلك، تذكر أن المصفوفة A ومحددتها والمصفوفة A’ هي:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

احسب

$\displaystyle z$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

وبالتالي فإن حل نظام المعادلات هو:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

المثال 2: نظام متوافق غير محدد (ICS)

حل نظام المعادلات التالي باستخدام قاعدة كرامر:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

الآن نحسب مدى المصفوفتين وبالتالي يمكننا معرفة نوع النظام. لحساب رتبة A، نحسب محدد المصفوفة بأكملها (باستخدام قاعدة ساروس) ونتحقق مما إذا كانت 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

المحدد يعطي 0، وبالتالي فإن المصفوفة A ليست من المرتبة 3. ولكن لديها محدد 2 × 2 يختلف عن 0:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

لذا فإن المصفوفة A لها المرتبة 2 :

$\displaystyle rg(A)=2$

بمجرد أن نعرف مدى المصفوفة A، نحسب مدى المصفوفة A’. محدد الأعمدة الثلاثة الأولى يعطي 0، لذلك جربنا المحددات الأخرى 3×3 في المصفوفة A’:

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

جميع محددات الرتبة 3 تعطي 0. لكن من الواضح أن المصفوفة A’ لها نفس المحدد غير 0 2×2 مثل المصفوفة A:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

وبالتالي فإن المصفوفة A’ هي أيضًا من المرتبة 2 :

$\displaystyle rg(A')=2$

لذا، بما أن رتبة المصفوفة A تساوي رتبة المصفوفة A’ لكن هاتين الرتبتين أصغر من عدد المجهولات في النظام (3)، فإننا نعرف من خلال نظرية روشيه-فروبينيوس أنه نظام متوافق بشكل غير محدد (المركز الدولي):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

عندما نريد حل نظام غير محدد متوافق (SCI)، نحتاج إلى تحويل النظام : نحذف المعادلة أولاً، ثم نحول متغيرًا إلى lect (عادةً المتغير z)، وأخيرًا نضع الحدود مع lect مع المصطلحات المستقلة.

بمجرد تحويل النظام، نطبق قاعدة كرامر وسنحصل على حل النظام كدالة لـ lect.

في هذه الحالة سوف نقوم بحذف المعادلة الأخيرة من النظام:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

الآن دعونا نحول المتغير z إلى lect:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

ونضع الحدود مع α مع الحدود المستقلة:

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

لذلك، تظل المصفوفة A والمصفوفة A’ للنظام كما يلي:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

أخيرًا، بمجرد أن نقوم بتحويل النظام، فإننا نطبق قاعدة كرامر . لذلك نحل محدد A :

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

في حين أن حل نظام المعادلات هو دالة لـ lect، نظرًا لأنه من SCI، وبالتالي فإن لديه عدد لا نهائي من الحلول:

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

قاعدة كريمر تحل المسائل

التمرين 1

طبق قاعدة كرامر لحل النظام التالي من معادلتين بمجهولين:

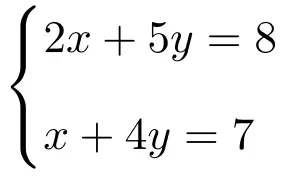
تم حل التمرين خطوة بخطوة باستخدام قاعدة كريمر 2×2

انظر الحل

أول ما يجب فعله هو المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

يجب علينا الآن العثور على رتبة المصفوفة A. للقيام بذلك، نتحقق مما إذا كان محدد المصفوفة بأكملها مختلفًا عن 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

نظرًا لأن المصفوفة لها محدد 2 × 2 يختلف عن 0، فإن المصفوفة A لها المرتبة 2:

$\displaystyle rg(A)=2$

بمجرد أن نعرف رتبة “أ”، فإننا نحسب رتبة “أ”. سيكون هذا على الأقل من الرتبة 2، لأننا رأينا للتو أنه يحتوي داخل محدد من الرتبة 2 يختلف عن 0. علاوة على ذلك، لا يمكن أن يكون من الرتبة 3، لأننا لا نستطيع عدم إنشاء محدد 3×3. ولذلك، فإن المصفوفة A’ هي أيضًا من المرتبة 2:

$\displaystyle rg(A')=2$

لذلك، من خلال تطبيق نظرية روشيه-فروبينيوس، نعلم أن هذا نظام محدد متوافق (SCD)، لأن مدى A يساوي نطاق A’ وعدد المجهولين.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

بمجرد أن نعرف أن النظام هو SCD، نطبق قاعدة كرامر لحلها.

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

وبالتالي فإن حل نظام المعادلات هو:

$\displaystyle \bm{x = -1 \qquad y=2}$

تمرين 2

أوجد حل النظام التالي المكون من ثلاث معادلات ذات ثلاثة مجاهيل باستخدام قاعدة كرامر:

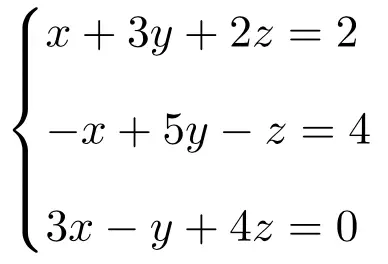
حل تمرين لقاعدة كرامر لنظام المعادلات 3x3

انظر الحل

نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

نجد الآن رتبة المصفوفة A عن طريق حساب محدد المصفوفة 3×3 بقاعدة ساروس:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

المصفوفة التي لها محدد من الرتبة 3 تختلف عن 0، المصفوفة A هي من المرتبة 3:

$\displaystyle rg(A)=3$

وبالتالي، فإن المصفوفة A’ هي أيضًا من المرتبة 3:

$\displaystyle rg(A')=3$

لذلك، باستخدام نظرية روشيه-فروبينيوس، نعلم أن هذا نظام محدد متوافق (SCD)، لأن مدى A يساوي نطاق A’ وعدد المجهولين.

بمجرد أن نعرف أن النظام هو SCD، نحتاج إلى تطبيق قاعدة كرامر لحل النظام.

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

احسب

$\displaystyle z$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

وبالتالي فإن حل نظام المعادلات هو:

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

التمرين 3

احسب حل النظام التالي المكون من ثلاث معادلات ذات ثلاثة مجاهيل باستخدام قاعدة كرامر:

انظر الحل

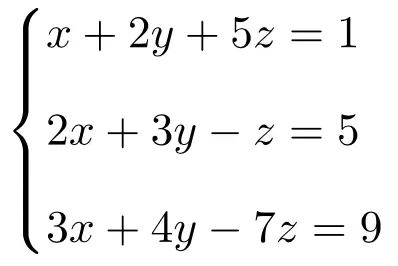
نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

جميع محددات الرتبة 3 تعطي 0. ومع ذلك، فإن المصفوفة A’ لها نفس المحدد 2×2 غير 0 مثل المصفوفة A:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

ولذلك، فإن المصفوفة A’ هي أيضًا من المرتبة 2:

$\displaystyle rg(A')=2$

بما أن رتبة المصفوفة A تساوي رتبة المصفوفة A’ ولكن هذين أقل من عدد المجهولين للنظام (3)، فإننا نعرف من خلال نظرية Rouché-Frobenius أنه نظام متوافق غير محدد (ICS):

كوننا نظام ICS، علينا إزالة المعادلة. في هذه الحالة سوف نقوم بحذف المعادلة الأخيرة من النظام:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

الآن دعونا نحول المتغير z إلى lect:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

ونضع الحدود مع α مع الحدود المستقلة:

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

بحيث تبقى المصفوفة A والمصفوفة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

أخيرًا، بمجرد أن نقوم بتحويل النظام، فإننا نطبق قاعدة كرامر . لذلك نحل محدد A :

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

في حين أن حل نظام المعادلات هو دالة لـ lect، نظرًا لأنه من SCI، وبالتالي فإن لديه عدد لا نهائي من الحلول:

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

التمرين 4

حل المسألة التالية لنظام من ثلاث معادلات ذات 3 مجاهيل بتطبيق قاعدة كرامر:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

انظر الحل

أولاً، نقوم ببناء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

الآن دعونا نحسب رتبة المصفوفة A عن طريق حساب محدد المصفوفة 3×3 باستخدام قاعدة ساروس:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

المصفوفة التي لها محدد من الرتبة 3 تختلف عن 0، المصفوفة A هي من المرتبة 3:

$\displaystyle rg(A)=3$

وبالتالي، فإن المصفوفة A’ هي أيضًا من المرتبة 3، حيث يجب أن تكون على الأقل من نفس رتبة المصفوفة A ولا يمكن أن تكون من المرتبة 4 لأنها مصفوفة البعد 3×4.

$\displaystyle rg(A')=3$

لذلك، باستخدام نظرية روشيه-فروبينيوس، نستنتج أنه نظام محدد التوافق (SCD)، لأن مدى A يساوي مدى A’ وعدد المجهولين.

بمجرد أن نعرف أن النظام هو SCD، نحتاج إلى تطبيق قاعدة كرامر لحل النظام.

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

احسب

$\displaystyle z$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثالث من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

وبالتالي فإن حل نظام المعادلات الخطية هو:

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

التمرين 5

حل نظام المعادلات الخطية التالي باستخدام قاعدة كرامر:

انظر الحل

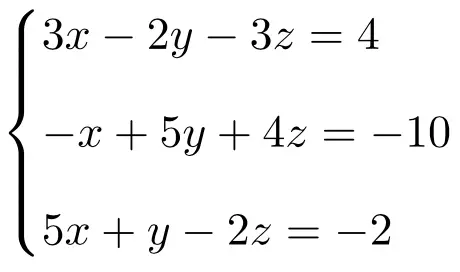
نقوم أولاً بإنشاء المصفوفة A والمصفوفة الموسعة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

نحسب مدى المصفوفة A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

جميع محددات الرتبة 3 تعطي 0. لكن من الواضح أن المصفوفة A’ لها نفس محدد الرتبة 2 بخلاف 0 مثل المصفوفة A:

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

ولذلك، فإن المصفوفة A’ هي أيضًا من المرتبة 2:

$\displaystyle rg(A')=2$

رتبة المصفوفة A تساوي رتبة المصفوفة A’ لكن هاتين المصفوفتين أصغر من عدد المجهولات في النظام (3)، لذلك من خلال نظرية Rouché-Frobenius نعرف أنه نظام غير محدد متوافق (SCI). :

كوننا نظام ICS، علينا حذف معادلة واحدة. في هذه الحالة سوف نقوم بحذف المعادلة الأخيرة من النظام:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

الآن دعونا نحول المتغير z إلى lect:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

ونضع الحدود مع α مع الحدود المستقلة:

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

بحيث تبقى المصفوفة A والمصفوفة A’ للنظام:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

أخيرًا، بمجرد أن نقوم بتحويل النظام، فإننا نطبق قاعدة كرامر . لذلك نحل محدد A:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

لحساب المجهول

$\displaystyle x$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الأول من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

لحساب المجهول

$\displaystyle y$

باستخدام قاعدة كرامر، نقوم بتغيير العمود الثاني من محدد A إلى عمود الحدود المستقلة ونقسمه على محدد A:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

وبالتالي، فإن حل نظام المعادلات هو دالة لـ lect، نظرًا لأنه من SCI، وبالتالي فإن النظام لديه عدد لا نهائي من الحلول:

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

حكم كريمر

ما هي قاعدة كريمر؟

مثال 1: تحديد النظام المتوافق (SCD)

المثال 2: نظام متوافق غير محدد (ICS)

قاعدة كريمر تحل المسائل

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد