الخطوط المتقاطعة - الماتوريتي

ستجد في هذه الصفحة كل شيء عن الخطوط القاطعة: ماذا تعني، الأنواع المختلفة الموجودة، كيفية معرفة ما إذا كان الخطان قاطعين، كيفية العثور على النقطة المشتركة بينهما،… ستتمكن أيضًا من رؤية العديد من الأمثلة والتمارين التي تم حلها من الخطوط القاطعة.

ما هما الخطان المتقاطعان؟

في الرياضيات، تعريف الخطوط القاطعة هو كما يلي:

يتقاطع خطان عندما يتقاطعان عند نقطة واحدة فقط. ولذلك فإن الخطوط المتقاطعة تشترك في نقطة واحدة فقط. علاوة على ذلك، يجب بالضرورة وجود خطين متقاطعين في نفس المستوى الديكارتي.

إن مفهوم الخطين اللذين يتقاطعان في نقطة واحدة مهم لأنه إذا كان لهما أكثر من نقطة تقاطع سيكونان خطين متوازيين، ومن ناحية أخرى، إذا لم يكن لهما نقطة تقاطع، سيكونان خطين متوازيين.

أمثلة على الخطوط المتقاطعة

بعد أن رأينا معنى الخطين المتقاطعين، دعونا الآن نلقي نظرة على مثالين مختلفين لهذا النوع من الخطوط:

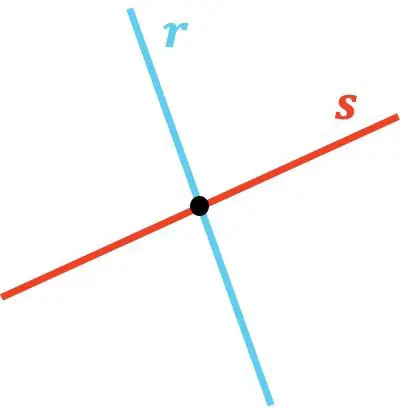
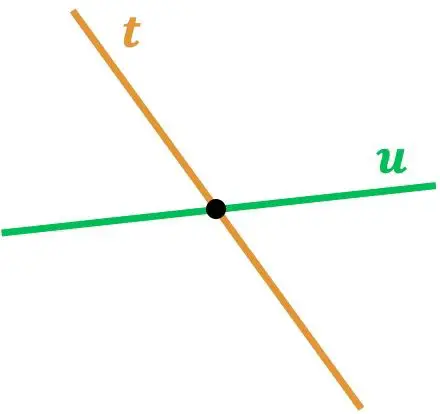
كما ترى، يتقاطع الخطان r و s لأنهما يتلامسان عند نقطة واحدة. وبنفس الطريقة، يتقاطع الخط t مع الخط u حيث أن هناك نقطة تقاطعهما.

أنواع الخطوط المتقاطعة

هناك نوعان من الخطوط المتقاطعة:

الخطوط المتعامدة : هي الخطوط التي تتقاطع بزاوية قائمة قدرها 90 درجة.
الخطوط المائلة: تتكون من خطوط تتقاطع بزاوية حادة بين 0 درجة و90 درجة (غير متضمنة).

خطوط مستقيمة متعامدة

الخطوط المتعامدة هي تلك الخطوط التي تتقاطع لتشكل أربع زوايا قياسها 90 درجة.

وبالمثل، فإن ميلي الخطين المتعامدين يحقق دائمًا الشرط التالي:

$m_r = -\cfrac{1}{m_s}$

خاصية أخرى للخطوط المتقاطعة المتعامدة هي أن حاصل الضرب النقطي بين متجهات اتجاهها (المتجه الذي يشير إلى اتجاه الخط) يساوي الصفر.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

إذا كنت مهتمًا أكثر بالخطوط المتعامدة، يمكنك في هذا الرابط مشاهدة أمثلة للخطوط المتعامدة . بالإضافة إلى ذلك، ستجد أيضًا كيفية حساب خط عمودي على خط آخر، وخصائص هذا النوع من الخطوط، وتمارين تم حلها خطوة بخطوة، وما إلى ذلك.

خطوط مائلة

الخطوط المائلة هي تلك الخطوط التي تتقاطع لتشكل زوايا حادة وزوايا منفرجة في أزواج. وهذا يعني أن نصنع زاويتين حادتين (أقل من 90 درجة) وزاويتين منفرجتين (أكبر من 90 درجة). ومع ذلك، وفقا لتعريف زاوية الخطين، فإن الزاوية بين الخطين هي أصغر الخطوط التي تشكلها.

يمكن حساب الزاوية بين خطين مائلين وميليهما باستخدام الصيغة التالية:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

كيف تعرف إذا كان الخطان متقاطعين؟

هناك ثلاث طرق أساسية للعثور على الموضع النسبي لخطين:

مع متجهات الاتجاه للخطين.
مع منحدرات الخطين.
مع المعادلة الضمنية (أو العامة) للخطين.

ثم سنرى شرح الطرق الثلاثة الموجودة لمعرفة متى يتقاطع الخطان.

من متجهات الاتجاه للخطوط

إذا كانت إحداثيات متجهات الاتجاه (المتجه الذي يحدد اتجاه الخط) لخطين مختلفين غير متناسبة ، فإن هذين الخطين يتقاطعان.

دعونا نرى تمرينًا تم حله خطوة بخطوة لخطين متقاطعين:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

يتم التعبير عن كلا الخطين كمعادلات بارامترية، وبالتالي فإن مكونات متجه الاتجاه لكل سطر هي الأرقام الموجودة أمام المعلمة

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

لذا، لمعرفة ما إذا كانت متجهات الاتجاه متناسبة، علينا تقسيم إحداثياتها فيما بينها. فإذا حصلنا على نفس النتيجة في كلا القسمين، فإنهما سيكونان متناسبين؛ ومن ناحية أخرى، إذا كانت النتيجة مختلفة، فهذا يعني أن المتجهات غير متناسبة.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

تقسيمات المكونات غير متكافئة، وبالتالي فإن المتجهات غير متناسبة وبالتالي تتقاطع الخطوط.

في بداية المنحدرات

إذا كان لخطين ميلان مختلفان ، فهذا يعني أن الخطين متقاطعان.

على سبيل المثال، يتقاطع الخطان التاليان لأن ميلهما مختلف:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

منحدر الخط

$r$

هو -2 ومنحدر الخط

$s$

هو 3.

$m_r =-2 \neq m_s =3$

بما أن الخطين ليس لهما نفس الميل، فهما متقاطعان.

من المعادلة الضمنية للخط

ويمكن أيضًا معرفة ما إذا كان الخطان متقاطعين أم لا من خلال المعادلات الضمنية (أو المعادلات العامة) للخطوط. المعادلة الضمنية للخط هي كما يلي:

$Ax+By+C=0$

وبالتالي، يتقاطع خطان عندما لا يكون معاملاهما A وB متناسبين.

دعونا نرى مثالاً لخطين متقاطعين معرفين بمعادلتهما الضمنية:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

وللتحقق من أن هذين الخطين متقاطعين، يجب علينا تحليل تناسب المعامل A (الرقم الموجود أمام المتغير

$x$

) مع المعامل B (الرقم الموجود أمام المتغير

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

المصطلحان غير متناسبين، لذا فإن الخطين يتقاطعان بشكل فعال.

أوجد النقطة المشتركة بين خطين متقاطعين

كما رأينا، الخطوط المتقاطعة تشترك في نقطة واحدة فقط. وبالتالي، لحساب نقطة تقاطع خطين قاطعين ، من الضروري حل نظام المعادلات التي يتكون منها الخطين.

على سبيل المثال، سنجد نقطة تقاطع الخطين التاليين:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

ولتحديد نقطة تقاطع الخطين يجب علينا حل نظام المعادلات الخطية المكونة من الخطين:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

في هذه الحالة، سوف نقوم بحل النظام بطريقة الاستبدال. لذلك سوف نقوم بعزل المتغير

$x$

من المعادلة الأولى ونعوض بها في المعادلة الثانية:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

وبمجرد أن نعرف كم يستحق المجهول

$y$

نعوض بقيمته في التعبير الموجود لـ

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

وبالتالي فإن حل نظام المعادلات هو نقطة تقاطع الخطين. وهذه النقطة هي

$\bm{(3,1)}.$

خط يتقاطع مع دائرة

عادة، عندما نقول إن خطين متقاطعين، فإننا نشير إلى المفهوم الذي رأيناه للتو. ومع ذلك، في الهندسة، هناك معنى آخر للخط القاطع:

الخط المتقاطع مع الدائرة هو الخط الذي يتقاطع مع الدائرة (أو المنحنى) عند نقطتين مختلفتين.

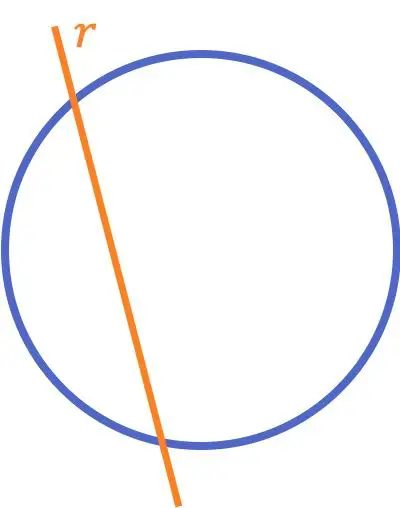
على عكس مفهوم الخطين المتقاطعين الذي يتم تدريسه عادة في المدرسة الابتدائية، فإن هذا التعريف للخط المتقاطع مع الدائرة غالبًا ما تتم دراسته في الفصول اللاحقة جنبًا إلى جنب مع جميع المواضع النسبية للخطوط مع الدوائر.

خطوط متقاطعة