من المؤكد أنك سمعت عن مجموعة الأعداد التخيلية أو الوحدة التخيلية. وهو مفهوم رياضي ينشأ من الحاجة الرياضية للتعبير عن أرقام لا تنتمي إلى الأعداد الحقيقية .
ما هي الأرقام الخيالية؟
الأعداد التخيلية هي تلك التي عند تربيعها تعطي رقما سالبا . ولذلك، فهذه قيم تعادل الجذر التربيعي لعدد سالب. على سبيل المثال، الوحدة التخيلية (الرقم i) تساوي الجذر التربيعي لـ -1.
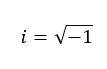
هذه الأرقام لا تنتمي إلى الأعداد الحقيقية، لأنه في المجموعة الحقيقية لا يمكن حل الجذور السالبة. وهنا تكمن أهمية الإعداد الخيالي. تم اختراع هذه المجموعة لتكون قادرة على التعامل مع الجذور السالبة ولتكون قادرة على حل جميع المعادلات والمسائل التربيعية التي “ليس لها حل”، لأنها تعطينا جذرًا سالبًا.
لتجنب الخلط، من المهم التمييز بين الأعداد التخيلية والأعدادالمركبة . المجمعات هي أعداد مكونة من عدد حقيقي وعدد وهمي . لذلك، فإن التخيلات هي فئة فرعية من المجمعات التي ليس لها جزء حقيقي. في الجدول التالي، ستتمكن من تقدير الاختلافات بشكل أفضل.
| عدد مركب | الحزب الملكي | جزء الخيال | وصف |
| 4+7ط | 4 | 7ط | معقد |
| 3 | 3 | 0 | ملكي نقي |
| 2ط | 0 | 2ط | محض خيال |
للانتهاء من تحديد موقع هذه المجموعة الرقمية، يمكننا أن نتصور في الصورة التالية هيكلًا لجميع المجموعات. كما نرى، تشمل الأعداد المركبة جميع أنواع الأعداد ، وهذه بدورها يمكن تقسيمها إلى أعداد حقيقية وأعداد خيالية خالصة (وهي التي نتعامل معها في هذه المقالة).

أمثلة على الأرقام التخيلية
ومن الوحدة التخيلية (i) يمكننا استنتاج أعداد خيالية أخرى. تحتاج فقط إلى تطبيق الصيغة التالية:
م = ري
حيث m هو عدد وهمي، r هو عدد حقيقي وi هي الوحدة التخيلية. في الصورة التالية يمكنك أن ترى كيف نحصل على تخيلات مختلفة من الجذور السلبية.
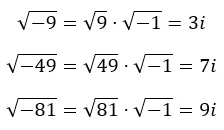
وفي الواقع يمكننا استقراء ذلك بالتعبير التالي:
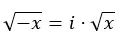
خصائص الأعداد التخيلية
الأعداد التخيلية لها عدد من الخصائص المثيرة للاهتمام . بعضها تحدثنا عنها بالفعل في بداية هذه المقالة والبعض الآخر لم نتحدث عنها:
- فالتخيلات لا تنتمي إلى مجموعة الحقائق، لأنها أرقام غير موجودة فيزيائيا ولا يمكن تمثيلها في واقعنا.
- هذه قيم تعادل الجذور السالبة.
- ويمكن تمثيلها بيانيا على الخط الوهمي.
- تعتبر القوى التخيلية (هذا المفهوم الذي سنشرحه في القسم التالي) مساعدة كبيرة في تبسيط الحسابات العددية التي تتضمن قيمًا خيالية.
- صيغة أويلر هي تعبير يسمح لك بربط الأعداد التخيلية بالأعداد الحقيقية.
العمليات على الأعداد التخيلية
الآن بعد أن عرفت جميع الخصائص المهمة للأعداد التخيلية، فقد حان الوقت لتعلم كيفية حل العمليات باستخدامها. للعمل مع القيم التخيلية ، يجب عليك اتباع نفس الخطوات التي تتبعها للعمل مع القيم الحقيقية، إلا أنه يجب أن تأخذ في الاعتبار مفهوم واحد: القوى التخيلية.
القوى الخيالية
تتمتع الأعداد التخيلية بخاصية مثيرة للاهتمام تحدث عند ضرب الوحدة التخيلية في نفسها. أي أن هذا يحدث عندما تصنع قوى الوحدة التخيلية . فإذا قمنا بكتابة القوى كما في القائمة التالية يمكن اكتشاف النمط:
ط 0 = 1
أنا 1 = أنا
i 2 = i · i = ( √ -1) · ( √ -1) = -1
أنا 3 = أنا 2 أنا = (-1) أنا = -i
ط 4 = أنا 2 أنا 2 = (-1) (-1) = 1
إن معرفة هذا المفهوم ستسهل علينا كثيرًا حل العمليات على الأعداد التخيلية، لأننا سنكون قادرين على تبسيط العمليات الصعبة وجعلها أسهل قليلاً. كما أن الشيء الجيد في هذه القوى هو أنها تتكرر إلى أجل غير مسمى. يمكننا أن نرى هذا إذا أضفنا المزيد من القوى:
أنا 5 = أنا
ط 6 = -1
ط 7 = -ط
ط 8 = 1
إلخ.
ومع القوى السلبية يحدث هذا أيضًا.
العمليات الحسابية على الأعداد التخيلية
بعد ذلك، سنقدم لك مثالاً على كل عملية حسابية أساسية، حتى تتمكن من رؤية حسابات الأعداد التخيلية التي تم حلها.
- إضافة أرقام خيالية: إنها تمامًا مثل إضافة أرقام حقيقية، لكن لا تنس إضافة i.
4ط + 3ط = 7ط
- طرح الأعداد التخيلية: يتم أيضًا حل عمليات الطرح بنفس الطريقة كما في المجموعة الحقيقية.
4ط – 3ط = أنا
- ضرب الأعداد التخيلية: وفي هذه الحالة يجب أن نأخذ في الاعتبار القوى التخيلية التي ذكرناها سابقاً.
3i 4i = 12 i 2 = 12 (-1) = -12
- قسمة الأعداد التخيلية: في هذا النوع من القسمة يجب علينا أيضًا أن نكون يقظين، في حالة مواجهة قوة خيالية، مما يسمح لنا بتبسيط العملية.
12ط ÷ 4ط = 3
المعادلات ذات الأعداد التخيلية
كما قلنا من قبل، عندما نحل المعادلات في المجموعة الحقيقية، أحيانًا نحصل على جذور سالبة، وبالتالي فإن المعادلات “ليس لها حل” . لكن الآن بعد أن عرفنا المتخيلات، أصبح بإمكاننا حل هذه المعادلات. دعونا نرى مثالا:
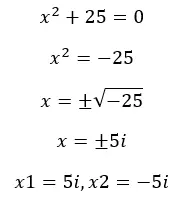
ما هي الأرقام الخيالية المستخدمة؟
تنشأ الأرقام الخيالية من الحاجة إلى القدرة على التعبير عن القيم التي تقع خارج المجموعة الحقيقية. لهذا السبب، في البداية، قد يبدو أنهم لا يملكون الكثير من التطبيقات المفيدة . لكن الحقيقة هي أن الأمر عكس ذلك تماما. لأنه عندما نجمعها مع الأعداد الحقيقية، نحصل على الأعداد المركبة.
وهذه لها تطبيقات كثيرة. يتم استخدامها لدراسة التيار المتردد (لأنه يحتوي على قيم سالبة)، كما أن استخدامه منتشر جدًا في مجال الموجات (التي لها تطبيقات في الفيزياء وإلكترونيات الاتصالات وميكانيكا الكم). من بين العديد من الاستخدامات الأخرى.
بالإضافة إلى ذلك، غالبًا ما يحدث أنه عندما تحل معادلة من الدرجة الثانية ، فإن القيمة تعطيك جذرًا سالبًا ولا يمكنك العمل… باستخدام التخيلات ، يمكنك حلها . لذا، كخاتمة، يمكننا القول إنها مجموعة تسمح لنا بتوسيع معرفتنا الأكثر تجريدًا.