ما هي قاعدة روفيني وكيف يتم استخدامها في الآلة الحاسبة؟

قاعدة روفيني هي إجراء رياضي تم تطويره بواسطة باولو روفيني ، والذي يسمح لنا بتقسيم كثيرات الحدود من الشكل (x – a). تُعرف هذه الطريقة الرياضية أيضًا بالتقسيم الاصطناعي. ولكن كيف يتم استخدام هذا الإجراء وما هي خطواته؟ وكيف تحل تمرين روفيني بالآلة الحاسبة؟ سنشرح لك كل هذا في هذه المقالة بطريقة مختصرة وسهلة الفهم ، بالإضافة إلى أننا سنوصي بأفضل الآلات الحاسبة لروفيني.

آلة حاسبة روفيني على الإنترنت

إذا كنت تريد تحليل كثيرة الحدود، يمكنك استخدام هذه الآلة الحاسبة، والتي ستسمح لك بتحليل أي تعبير ، طالما أنك تكتبه باستخدام الرموز التالية: ^ (رفع) و / (تقسيم). ويمكنك أن تطمئن، لأن هذه الآلة الحاسبة قادرة على تحليل متعددات الحدود من الدرجة 3 وحتى الدرجات الأعلى. ولذلك فهي أداة الحساب النهائية لتحليل كثيرات الحدود عبر الإنترنت.

كيفية تطبيق روفيني؟

سنشرح في هذا القسم كيفية تنفيذ Ruffini وسنقوم بحل مثال محدد باستخدام الطريقة، وبهذه الطريقة ستتمكن من رؤية الإجراء بأكمله بوضوح ورسوم بيانية. مما سيسمح لك بفهم هذا المفهوم من جذوره وسوف تتذكره لاحقًا في الامتحان. بالإضافة إلى ذلك، قمنا بتضمين فيديو توضيحي يسمح لك بفهم هذا المفهوم حتى لو كانت لديك شكوك مع الشرح المكتوب.

متطلبات استخدام طريقة روفيني

قبل أن تبدأ في حل قسمة كثيرات الحدود أو قبل تحليل كثيرات الحدود ، عليك أن تنظر إلى المقسوم عليه. إذا كانت من الدرجة الأولى فيمكننا المتابعة بطريقة روفيني. من ناحية أخرى، إذا كان المقسوم عليه بدرجة أكبر من 1، فلن نتمكن من حل العملية الحسابية باتباع هذا الإجراء. ولذلك، علينا استخدام أي طريقة أخرى لتقسيم كثيرات الحدود. وهذا عامل يجب التحقق منه قبل البدء في إجراء الحسابات، وإلا قد تضيع الكثير من الوقت.

إجراء قسمة كثيرات الحدود باستخدام قاعدة روفيني

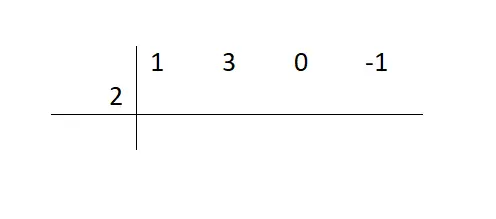
الآن بعد أن عرفنا متى يمكن استخدام هذا المورد الرياضي، سنرى الخطوات المختلفة التي يجب اتباعها حتى نتمكن من تحليل كثيرة الحدود. إذن، من المثال (x³+3x²-1) / (x-2)، يجب علينا أولًا كتابة معاملات المقسوم على خط أفقي، يمثل الحدود المفقودة بصفر. وبعد ذلك، سنضع الحد المستقل للمقسوم عليه في علامة المقابل المنفصلة، كما هو موضح في الصورة.

ثم يجب علينا خفض المعامل الأول (الذي يصاحب المتغير المرفوع إلى أس أعلى). لن نفعل شيئًا بهذا الرقم، بل سنقلله وننتقل إلى الخطوة التالية.

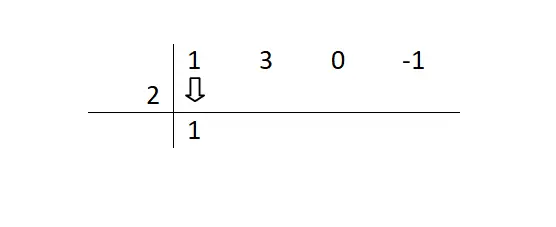
بعد ذلك، سنبدأ بسلسلة من الخطوات المتكررة إلى حد ما: سنضرب الرقم الذي خفضناه بالمقسوم عليه وسنضع النتيجة تحت الحد التالي. ثم سنضيف الحد التالي بين هذه النتيجة ونكتبه بجوار الرقم الأول الذي كتبناه.

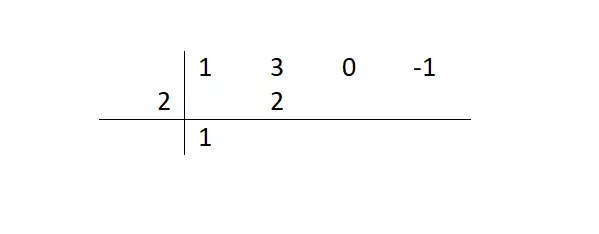
إذا اتبعنا هذا التسلسل من الخطوات حتى نكمل الجدول، فسيكون لدينا التصميم التالي. بهذه الطريقة سنعرف أن الباقي يساوي 19 (آخر رقم قمنا بحسابه) وأن تعبير الباقي (الحاصل) سيكون x²+5x+10. كل هذه المعلومات حصلنا عليها من الأرقام الموجودة في الصف السفلي . وفي حالة تحليل كثيرة الحدود، علينا استخدام خارج القسمة هذا للاستمرار في إيجاد الجذور الأخرى.

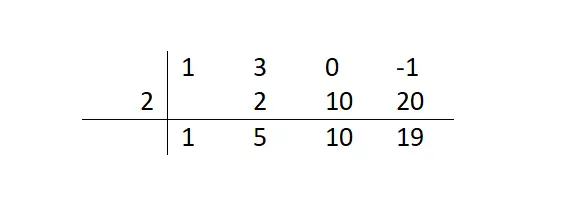
كيفية وضع روفيني في الآلة الحاسبة؟

لتتمكن من قسمة كثيرات الحدود باستخدام Ruffini على الآلة الحاسبة ، ما عليك سوى الوصول إلى أدوات حل الآلة الحاسبة، أي الوصول إلى وضع حساب المعادلة. وبمجرد الدخول، سنختار خيار المعادلات كثيرة الحدود، لأننا نريد تحليل كثيرة الحدود. بعد ذلك سوف نختار درجة التعبير ويمكننا الدخول إلى المحرر الرياضي، وبالتالي سوف نقوم بإدخال التعبير. لذا عندما نحصل على جذور كثيرة الحدود، كل ما علينا فعله هو كتابتها على الصورة (x – a). هذا الإجراء بأكمله (باستثناء الجزء الجذري) مطابق للإجراء الذي سنستخدمه لحل المعادلات باستخدام الآلة الحاسبة .

أفضل الآلات الحاسبة لحساب نظرية روفيني

يمكننا حاليًا العثور على العديد من الآلات الحاسبة القادرة على حل العمليات مع كثيرات الحدود وتحليلها. ومع ذلك، هناك بعض النماذج التي تبرز من حيث سهولة الاستخدام والسعر . هناك مثالان جيدان هما Casio FX-991SPX II و Casio FX-991ES PLUS ، في الواقع يعتمد الشرح الذي قدمناه في القسم السابق على تشغيل هذين الطرازين. على الرغم من أنه كما قلنا من قبل، يمكنك العثور على آلات حاسبة علمية أخرى ستساعدك أيضًا على القيام بـ Ruffini بشكل مثالي.

أمثلة وتمارين روفيني

يمكن ممارسة قاعدة روفيني عن طريق أخذ كثيرتي الحدود بشكل عشوائي، طالما أنهما يتبعان القواعد التي علقنا عليها في البداية. على الرغم من أنه يمكنك أيضًا تجربة تحليل كثيرات الحدود ذات الدرجة الأكبر من الواحد من خلال هذا الإجراء الرياضي. وبالتالي، ستراجع نفس الآلية الرياضية، وستقوم بدورها بمراجعة مفهوم جذر كثيرة الحدود. بعد ذلك، سنعرض لك كثيرتي حدود ستحتاج إلى تحليلهما وقسمة بسيطة إلى حد ما، والتي ستحتاج إلى حلها باستخدام طريقة روفيني.

التمرين 1

عامل متعدد الحدود: 2x³-7x²+8x-3

الجذور: x=1 وx=1، وبالتالي يتبقى لدينا (x-1)²(2x-3)

تمرين 2

عامل متعدد الحدود: x³+2x²-x-2

الجذور: x=-2، x=-1، x=1، لذلك سيتبقى لدينا (x+2)(x+1)(x-1)

التمرين 3

حل التقسيم التالي بين كثيرات الحدود: (3x³-5x²+2) / (x-2)

حاصل القسمة: 3x²+x+2، الباقي: 6

إذا كنت تريد المزيد من تمارين روفيني، ننصحك بمشاهدة مقالة Superprof هذه ، والتي تشرح نفس الإجراءات المذكورة في هذه المقالة. ولكن، مع الأمثلة والتمارين المختلفة قليلاً عن Ruffini، قد تتمكن من حل بعض الشكوك بمزيد من الممارسة. وفي كلتا الحالتين، نأمل أن تجد المحتوى الخاص بنا وآلة حاسبة Ruffini مفيدًا.