الفائدة البسيطة هي الطريقة الأكثر شيوعًا لحساب الفائدة، ويتم استخدامها لمجموعة متنوعة من الأغراض، بدءًا من شراء منزل وحتى الحصول على قرض شخصي. إذا كنت بحاجة إلى حساب الفائدة البسيطة، فسيوضح لك هذا الدليل كيفية القيام بذلك خطوة بخطوة. كما نوفر لك آلة حاسبة عبر الإنترنت لتسهيل مهمتك.
حاسبة الفائدة البسيطة
حاسبة الفائدة البسيطة عبر الإنترنت هي أداة يمكنها مساعدتك في حساب أي من المتغيرات المشاركة في حساب الفائدة البسيطة. لاستخدامه، ما عليك سوى تحديد ما تريد حسابه وإدخال البيانات الخاصة بالمتغيرات التي تطلبها. ثم عليك النقر على زر الحساب وهذا كل شيء.
ما هي الفائدة البسيطة؟
الفائدة البسيطة هي سعر الفائدة الذي يتم فرضه عند استثمار أو إقراض مبلغ لفترة زمنية محددة. ويتم حسابه عن طريق ضرب المبلغ الأولي في سعر الفائدة والوقت. وباختصار، يتم استخدام هذه الفائدة في الإجراءات المالية الثابتة والقصيرة الأجل عادة.
وبما أن سعر الفائدة والفترة الزمنية يظلان ثابتين، فإن الفائدة التي يجب دفعها شهريًا أو سنويًا هي نفسها دائمًا ، حيث لا تزيد الفائدة. هذا هو الفرق الرئيسي بين الفائدة البسيطة والفائدة المركبة .
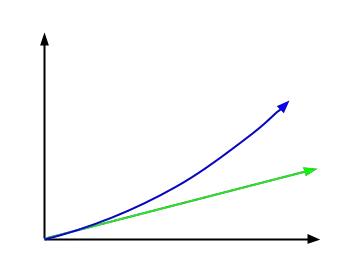
في الصورة التالية يمكنك رؤية الدالة التي تمثل الفائدة البسيطة باللون الأخضر ودالة الفائدة المركبة الموضحة باللون الأزرق. وكما نرى في الصورة، فهو ذو شكل أسي أكثر بكثير.
صيغة لحساب الفائدة البسيطة
صيغة حساب الفائدة البسيطة هي: I = C xixt ، حيث تتدخل المتغيرات التالية:
- رأس المال الأولي (C): مجموع الأموال المستثمرة أو المقترضة، والتي تحسب عليها الفائدة البسيطة.
- سعر الفائدة (ط): يخبرنا هذا المؤشر كنسبة مئوية بمبلغ الفائدة بالنسبة للوقت. من المهم كتابتها بواحد في الصيغة (تقسيم قيمة النسبة المئوية على مائة).
- الوقت (t): طول فترة الاستثمار، معبرًا عنها عمومًا بالسنوات. على الرغم من أننا سنعلمك أدناه كيفية تحويلها إلى وحدات زمنية أخرى، مثل: الأشهر والأيام.
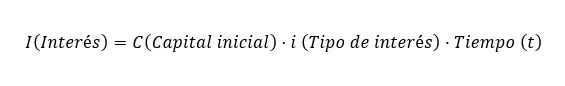
لمعرفة كيفية استخدام هذه الصيغة، يمكننا النظر في المثال التالي : لقد استثمرنا 1000 يورو بمعدل سنوي قدره 4٪، وبعد ثلاث سنوات، ما مقدار الفائدة التي سنحصل عليها؟ للعثور على الفائدة المتولدة، يجب علينا تطبيق الصيغة: I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = 120 يورو.
بعد ذلك، من الصيغة الرئيسية، يمكننا عزل المتغيرات المختلفة وبالتالي نحصل على الصيغ التي تسمح لنا بحساب رأس المال الأولي، وسعر الفائدة، والوقت ورأس المال النهائي. وهذا ما سنراه في الأقسام التالية، حيث سنعلمك كيفية حساب هذه المتغيرات من صيغة سبق أن رأيتها وأخرى بسيطة للغاية.
كيف يتم حساب رأس المال النهائي؟
لحساب رأس المال النهائي ، ببساطة قم بتطبيق المنطق. ثم، بما أن المبلغ النهائي يساوي المبلغ الأولي، بمجرد تطبيق الفائدة، فإن صيغتها هي: رأس المال النهائي (Cf) = رأس المال الأولي (C) + الفائدة (I). هذا التعبير هو ثاني أهم صيغة فائدة بسيطة، والأهم هو الصيغة السابقة.
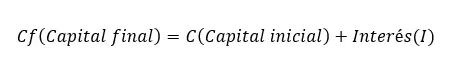
الآن بعد أن عرفت الصيغة، حاول حل هذا المثال العملي: ما هو رأس المال النهائي الذي ستحصل عليه إذا استثمرت 50,000 يورو لمدة 4 سنوات، بفائدة قدرها 20,000 يورو؟ ببساطة، نطبق التعبير السابق : رأس المال النهائي (Cf) = رأس المال الأولي (C) + الفائدة (I) = 50,000 + 20,000 = 70,000 يورو.
كيف يتم حساب رأس المال الأولي؟
إذا أردنا حساب رأس المال الأولي، فيمكننا استخدام صيغتين، اعتمادًا على البيانات التي يقدمونها لنا. أولاً، يمكننا تطبيق التعبير من القسم السابق إذا كان لدينا رأس المال النهائي والمبلغ الناتج عن الفائدة: رأس المال الأولي (C) = رأس المال النهائي (Cf) – الفائدة (I).
ثانياً، يمكننا عزل قيمة رأس المال الأولي بصيغة الفائدة البسيطة (التي تحدثنا عنها في البداية). وبالتالي سيتبقى لدينا رأس المال الأولي (C) = الفائدة (I) ÷ (الوقت (t) × سعر الفائدة (i)).

دعونا نرى مثالاً على الحالة الثانية الأكثر تعقيدًا: ما هو المبلغ الذي يجب أن أستثمره للحصول على فائدة بقيمة 30 ألف يورو، بمعدل 8٪ لمدة عامين؟ نطبق صيغة رأس المال الأولي = I ÷ (tx (i ÷ 100))، مما يترك لدينا 30,000 ÷ (2 x (8 ÷ 100)) = 187,500 يورو أوليًا.
كيف يتم حساب سعر الفائدة؟
لحساب سعر الفائدة ، يجب علينا أيضًا استخدام صيغة الفائدة البسيطة، ولكن مع عزل i. لذلك، يتبقى لدينا: سعر الفائدة (i) = الفائدة (I) ÷ (رأس المال الأولي (C) × الوقت (t)). كما ترون، جميع الصيغ هي نفسها، ولكن مع عزل متغير مختلف.
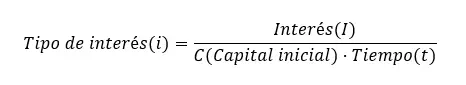
فيما يلي حالة عملية لحساب أسعار الفائدة: بأي سعر فائدة يجب أن نستثمر مبلغ 180 ألف يورو لمدة 5 سنوات، إذا أردنا تحويله إلى 200 ألف يورو؟ في هذا المثال، يجب عليك أولاً العثور على الفائدة: I = Cf – C = 200,000 – 180,000 = 20,000 يورو. ومن ثم نحل: سعر الفائدة = 20,000 ÷ (180,000 × 5) = 0.022 × 100 = 2.2%.
كيف يتم حساب الوقت؟
أخيرًا، يمكننا حساب الوقت ، والذي يمكن الحصول عليه أيضًا من الصيغة الأولية: الوقت (t) = الفائدة (I) ÷ (المبلغ الأولي (C) × سعر الفائدة (i)). من المهم أن تتذكر أن الصيغة تتطلب أن تكون وحدات الوقت سنوات. ومع ذلك، إذا كنت تريد التعبير عنها بوحدات أخرى، فيمكنك استخدام الأشكال التالية من الصيغة:
- I = C · (i / 100) · t إذا كانت t سنوات (صيغة عامة)
- I = C · (i / 1200) · t إذا كانت t أشهر (النتيجة بالأشهر)
- I = C · (i / 36000) · t إذا كانت t أيام (النتيجة بالأيام)
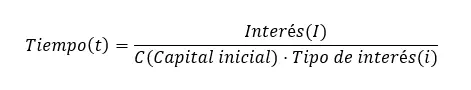
انظر إلى المثال التالي: كم من الوقت يجب أن يمر إذا أردنا استثمار مبلغ 40,000 يورو لتوليد فائدة قدرها 5,000 يورو، بمعدل 5%؟ ويبقى الحساب: الوقت = 5000 ÷ (40000 × 5 ÷ 100) = 2.5 سنة. لكن إذا أردنا حسابها بالأشهر يمكننا القيام بما يلي: الزمن = 5000 ÷ (40000 × 5 ÷ 1200) = 30 شهرًا.
مثال واقعي لحساب الفائدة البسيطة
لقد رأيت الآن مثالاً لحساب كل متغير يشكل معادلة الفائدة البسيطة. ومع ذلك، نريد أن نعرض لك مثالًا أخيرًا على الحساب الأكثر شيوعًا ، وهو حساب الفائدة نفسه. من أجل تطبيق الصيغة الأولى، سيكون لديك بقايا الطعام. إذا كنت تريد مراجعة الحساب، فإليك دراسة الحالة:
نحن نقترض 10000 يورو للاستثمار ونريد حساب مقدار الأموال التي سيتعين علينا سدادها بعد 5 سنوات إذا طلبوا منا فائدة سنوية بنسبة 3٪. الحساب سيكون:
10000 × 0.03 = 300
300 × 5 سنوات = 1500 يورو
CF = 10,000 يورو + 1,500 يورو = 11,500 يورو
وبالتالي، في نهاية 5 سنوات ستكون الفائدة 1500 يورو ورأس المال النهائي الذي سيتم دفعه هو 11500 يورو .
خاتمة
باختصار، لحساب الفائدة البسيطة ، يجب أن تأخذ في الاعتبار مبلغ القرض وسعر الفائدة والمدة. ومن هناك، يمكنك ببساطة ضرب هذه الأرقام الثلاثة للحصول على المبلغ الإجمالي للفائدة المستحقة الدفع. وإذا كنت تريد حساب أحد المتغيرات الأخرى، فبدلاً من الفائدة، تحتاج فقط إلى عزل تلك القيمة في الصيغة العامة.