مصفوفة يعقوبية ويعقوبية

ستجد في هذه الصفحة ما هي مصفوفة جاكوبي وكيفية حسابها باستخدام مثال. بالإضافة إلى ذلك، لديك العديد من التمارين التي تم حلها على المصفوفات اليعقوبية حتى تتمكن من التدرب عليها. سترى أيضًا سبب أهمية محدد المصفوفة اليعقوبية، اليعقوبية. وأخيرا، نوضح العلاقات التي تقيمها هذه المصفوفة مع العمليات الأخرى والتطبيقات التي لها.

ما هي المصفوفة اليعقوبية؟

تعريف المصفوفة اليعقوبية هو كما يلي:

مصفوفة جاكوبي هي مصفوفة مكونة من مشتقات جزئية من الدرجة الأولى للدالة.

وبالتالي فإن صيغة المصفوفة اليعقوبية هي كما يلي:

ولذلك، فإن مصفوفات جاكوبي ستحتوي دائمًا على عدد من الصفوف مثل الدوال العددية

$(f_1,f_2,\ldots ,f_m)$

لديك الوظيفة، وسوف يتوافق عدد الأعمدة مع عدد المتغيرات

$(x_1, x_2, \ldots , x_n).$

من ناحية أخرى، تُعرف هذه المصفوفة أيضًا بالخريطة التفاضلية اليعقوبية أو الخريطة الخطية اليعقوبية . في الواقع، أحيانًا يتم كتابته أيضًا بالحرف D بدلاً من الحرف J:

$\displaystyle J_f = D_f$

ومن باب الفضول، تم تسمية المصفوفة اليعقوبية على اسم كارل غوستاف جاكوبي، وهو عالم رياضيات وأستاذ مهم في القرن التاسع عشر قدم مساهمات مهمة في عالم الرياضيات، وخاصة في مجال الجبر الخطي.

مثال لحساب المصفوفة اليعقوبية

بمجرد أن نرى مفهوم المصفوفة اليعقوبية، سنرى خطوة بخطوة كيفية حسابها باستخدام مثال:

حدد المصفوفة اليعقوبية عند النقطة (1،2) للدالة التالية:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

أول شيء يتعين علينا القيام به هو حساب جميع المشتقات الجزئية من الدرجة الأولى للدالة:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

الآن نطبق صيغة المصفوفة اليعقوبية. في هذه الحالة، تحتوي الدالة على متغيرين ودالتين عدديتين، وبالتالي فإن المصفوفة اليعقوبية ستكون مصفوفة مربعة البعد 2×2:

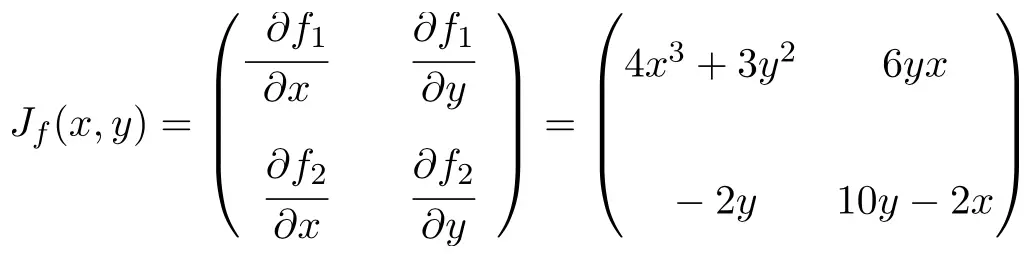
بمجرد أن نحصل على تعبير المصفوفة اليعقوبية، نحسبه عند النقطة (1،2):

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

وأخيرًا نقوم بتنفيذ العمليات ونحصل على الحل:

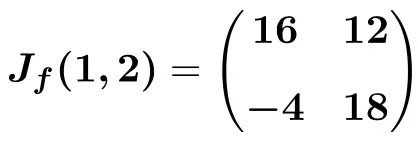
بمجرد أن تعرفت على كيفية العثور على المصفوفة اليعقوبية للدالة، نترك لك العديد من التمارين التي تم حلها خطوة بخطوة حتى تتمكن من التدرب عليها.

حل مسائل المصفوفات اليعقوبية

التمرين 1

أوجد المصفوفة اليعقوبية عند النقطة (0,-2) للدالة المتجهة التالية في متغيرين:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

انظر الحل

تحتوي الدالة على متغيرين ودوالتين عدديتين، وبالتالي فإن المصفوفة اليعقوبية ستكون مصفوفة مربعة بحجم 2×2:

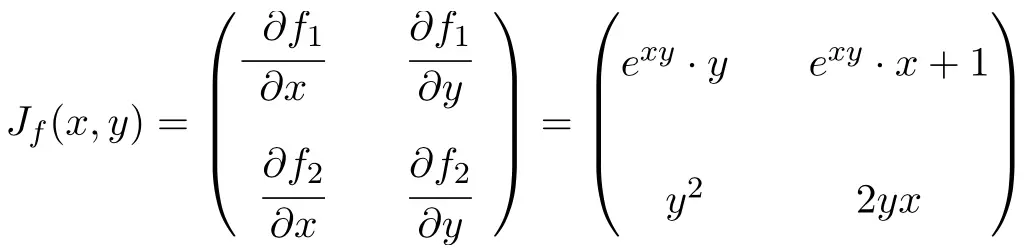
بمجرد أن نحسب التعبير الخاص بمصفوفة جاكوبي، نقيمه عند النقطة (0،-2):

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

وأخيرا نقوم بتنفيذ العمليات ونحصل على النتيجة:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

تمرين 2

احسب المصفوفة اليعقوبية عند النقطة (2،-1) للدالة التالية بمتغيرين:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

انظر الحل

في هذه الحالة، تحتوي الدالة على متغيرين ودوالتين عدديتين، وبالتالي فإن مصفوفة جاكوبي ستكون مصفوفة مربعة من الرتبة 2:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

بمجرد العثور على التعبير الخاص بالمصفوفة اليعقوبية، نحسبه عند النقطة (2،-1):

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

وأخيرا نقوم بتنفيذ العمليات ونحصل على النتيجة:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

التمرين 3

حدد المصفوفة اليعقوبية عند النقطة (2،-2،2) للدالة التالية بثلاثة متغيرات:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

انظر الحل

في هذه الحالة، تحتوي الدالة على ثلاثة متغيرات ودالتين عدديتين، وبالتالي فإن المصفوفة اليعقوبية ستكون مصفوفة مستطيلة البعد 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

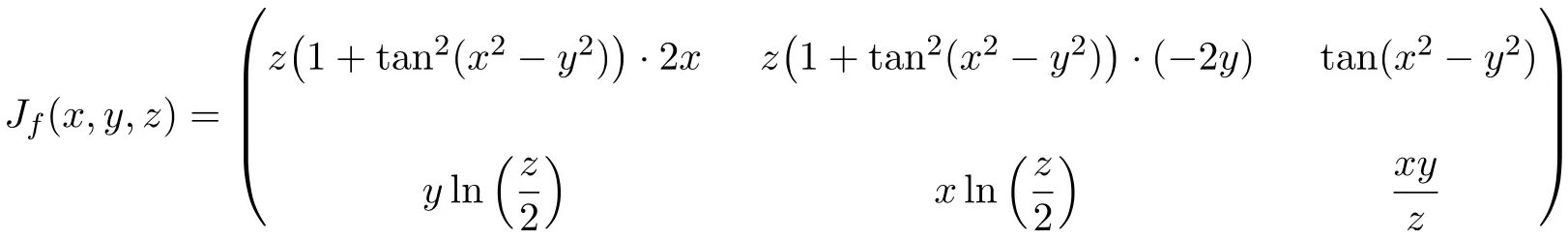
حل تمرين المصفوفة اليعقوبية لثلاثة متغيرات

بمجرد أن نحصل على التعبير الخاص بمصفوفة جاكوبي، فإننا نحسبه عند النقطة (2،-2،2):

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

نقوم بإجراء الحسابات:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

ونحن نواصل العمل حتى لم يعد من الممكن تبسيطه:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

التمرين 4

تحديد المصفوفة اليعقوبية عند هذه النقطة

$(\pi, \pi)$

للوظيفة متعددة المتغيرات التالية:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

انظر الحل

في هذه الحالة، تحتوي الدالة على متغيرين وثلاث دوال عددية، وبالتالي فإن المصفوفة اليعقوبية ستكون مصفوفة مستطيلة البعد 3×2:

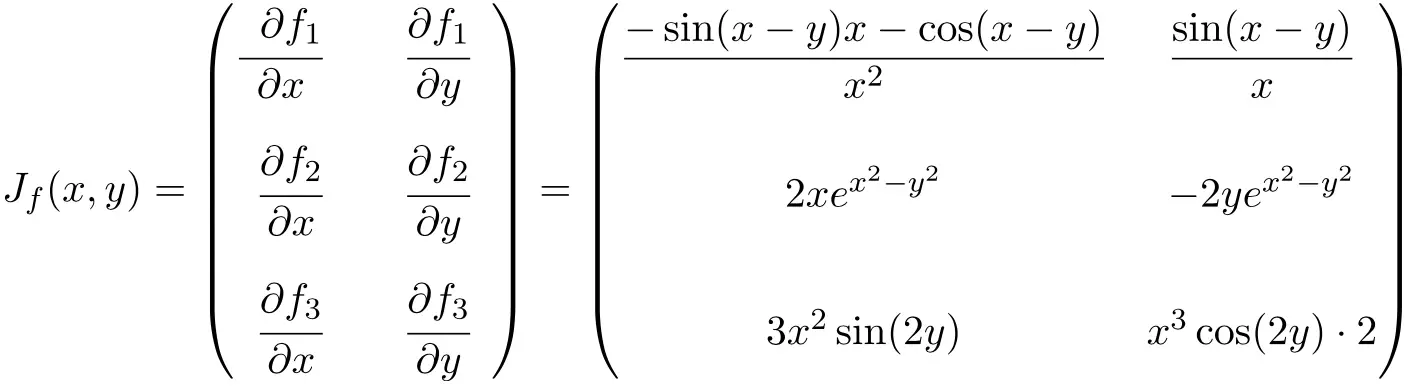
بمجرد أن نحصل على تعبير المصفوفة اليعقوبية، فإننا نوجد قيمة هذه المصفوفة

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

نقوم بتنفيذ العمليات:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

وبالتالي فإن المصفوفة اليعقوبية لوظيفة المتجه عند النقطة قيد النظر تستحق:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

التمرين 5

احسب المصفوفة اليعقوبية عند هذه النقطة

$(3,0,\pi)$

للدالة التالية مع 3 متغيرات:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

انظر الحل

في هذه الحالة، تكون الدالة مكونة من ثلاثة متغيرات وثلاث دوال عددية، وبالتالي فإن المصفوفة اليعقوبية ستكون مصفوفة مربعة البعد 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

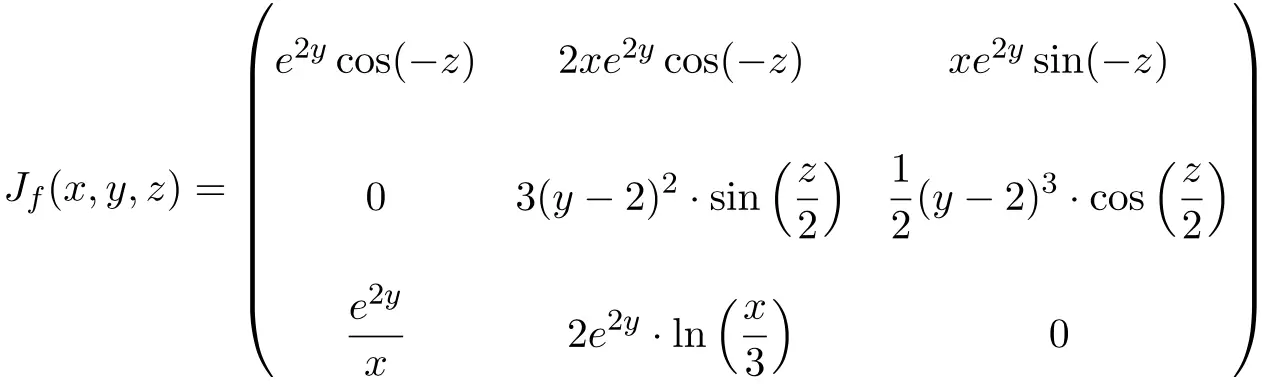
حل تمرين للمصفوفة اليعقوبية 3×3 مع 3 متغيرات

بمجرد العثور على مصفوفة جاكوبي، نقيمها عند النقطة

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

نحسب العمليات:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

ونتيجة المصفوفة اليعقوبية عند هذه النقطة هي:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

محدد المصفوفة اليعقوبية: اليعقوبية

محدد المصفوفة اليعقوبية يسمى المحدد اليعقوبي أو اليعقوبي. يجب أن يؤخذ في الاعتبار أنه لا يمكن حساب دالة جاكوبي إلا إذا كانت الدالة تحتوي على نفس عدد المتغيرات مثل الدوال العددية، لأن مصفوفة جاكوبي ستكون لها نفس عدد الصفوف مثل الأعمدة، وبالتالي ستكون مربعًا مصفوفة. .

المثال اليعقوبي

دعونا نرى مثالاً لحساب المحدد اليعقوبي لدالة ذات متغيرين:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

نحسب أولاً مصفوفة جاكوبي للدالة:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

والآن نحل محدد المصفوفة 2×2:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

اليعقوبي وانعكاس الوظيفة

الآن بعد أن رأيت مفهوم اليعقوبي، ربما فكرت… حسنًا، ما المغزى من ذلك؟

حسنًا، الاستخدام الرئيسي للجاكوبيان هو تحديد ما إذا كان من الممكن عكس الدالة. تقول نظرية الدالة العكسية أنه إذا كان محدد المصفوفة اليعقوبية (الجاكوبية) يختلف عن 0، فهذا يعني أن هذه الدالة قابلة للعكس.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

تجدر الإشارة إلى أن هذا الشرط ضروري ولكنه غير كاف، أي أنه إذا كان المحدد غير صفر فيمكننا الجزم بأن المصفوفة يمكن قلبها، أما إذا كان المحدد 0 فلا يمكننا معرفة ما إذا كان المحدد هو صفر أم لا. الدالة لها معكوس أو لا

على سبيل المثال، في المثال الذي رأيناه سابقًا حول كيفية العثور على اليعقوبي للدالة، فإن المحدد يعطي

$4x^2+4y^2$

. في هذه الحالة يمكننا الجزم بأن الدالة يمكن دائما أن تكون معكوسة إلا عند النقطة (0,0)، حيث أن هذه النقطة هي الوحيدة التي يساوي فيها المحدد اليعقوبي الصفر، وبالتالي لا نعرف ما إذا كانت الدالة العكسية أم لا موجود في هذه النقطة.

علاقة المصفوفة اليعقوبية بالعمليات الأخرى

ترتبط المصفوفة اليعقوبية بالتدرج ومصفوفة هسه للدالة:

ميل

إذا كانت الدالة دالة عددية، فستكون المصفوفة اليعقوبية عبارة عن مصفوفة صفية والتي ستكون مكافئة للتدرج :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

مصفوفة هسه

المصفوفة اليعقوبية لتدرج الدالة تساوي مصفوفة هسه :

$\displaystyle H_f = J(\nabla f)$

تعتبر الهسي مصفوفة مهمة جداً لاشتقاق الدوال ذات أكثر من متغير، لأنها تتكون من المشتقات الثانية للدالة. في الواقع، يمكن للمرء أن يقول أن مصفوفة هسه هي استمرارية المصفوفة اليعقوبية. ولكن من المهم جدًا أن يكون لدينا صفحة كاملة تشرح ذلك بالتفصيل. لذلك، إذا كنت تريد أن تعرف بالضبط ما هي هذه المصفوفة ولماذا هي مميزة جدًا، يمكنك النقر فوق الرابط.

تطبيقات على المصفوفة اليعقوبية

إلى جانب الفائدة التي رأيناها من المصفوفة اليعقوبية، والتي تحدد ما إذا كانت الدالة قابلة للعكس، فإن لمصفوفة جاكوبي تطبيقات أخرى.

يتم استخدام مصفوفة جاكوبي لحساب النقاط الحرجة للدالة متعددة المتغيرات، والتي يتم تصنيفها بعد ذلك إلى نقاط عظمى أو صغرى أو نقاط سرج من خلال مصفوفة هسه. للعثور على النقاط الحرجة، تحتاج إلى حساب مصفوفة جاكوبي للدالة، وتسويتها بالصفر، وحل المعادلات الناتجة.

$\displaystyle J_f(x)=0$

بالإضافة إلى ذلك، يوجد تطبيق آخر للمصفوفة اليعقوبية في تكامل الدوال مع أكثر من متغير، أي في التكاملات الثنائية والثلاثية وغيرها. حيث أن محدد المصفوفة اليعقوبية يسمح بتغيير المتغير في التكاملات المتعددة حسب الصيغة التالية:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

حيث T هي دالة التغيير المتغير التي تربط المتغيرات الأصلية بالمتغيرات الجديدة.

وأخيرًا، يتم استخدام مصفوفة جاكوبي أيضًا لإجراء تقريب خطي لأي دالة

$f$

حول نقطة

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

ما هي المصفوفة اليعقوبية؟

مثال لحساب المصفوفة اليعقوبية

حل مسائل المصفوفات اليعقوبية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

محدد المصفوفة اليعقوبية: اليعقوبية

المثال اليعقوبي

اليعقوبي وانعكاس الوظيفة

علاقة المصفوفة اليعقوبية بالعمليات الأخرى

ميل

مصفوفة هسه

تطبيقات على المصفوفة اليعقوبية

اترك تعليقاً إلغاء الرد