رقم أويلر (المعروف أيضًا باسم ثابت أويلر) هو رقم رياضي مهم وأساسي في مجالات مختلفة من الرياضيات، بما في ذلك نظرية الأعداد والطوبولوجيا ونظرية المجموعة ونظرية الوظيفة. ويرمز له بالحرف اليوناني “e” وقيمته التقريبية هي 2.71828.
الرقم e يتبع من صيغة الدالة الأسية وهو رقم أساسي في نظرية الأعداد المركبة.
وهو أيضًا عدد طبيعي يظهر في حل العديد من المسائل الرياضية، بما في ذلك حساب الاحتمالات ونمذجة عمليات النمو والاضمحلال.
ما هو أصل رقم أويلر؟
سمي رقم أويلر نسبة إلى عالم الرياضيات السويسري ليونارد أويلر (1707-1783)، الذي كان أحد أعظم علماء الرياضيات على مر العصور ويعتبر أبو الرياضيات الحديثة.
قدم أويلر مساهمات قيمة في العديد من مجالات الرياضيات، بما في ذلك نظرية الأعداد والهندسة وحساب التفاضل والتكامل والفيزياء وعلم الفلك.
كان هو أول من حدد واستخدم الرقم e (المسمى برقم أويلر) في عمله على حساب ونظرية اللوغاريتمات. تعدصيغة أويلر للأعداد المركبة أيضًا واحدة من أبرز مساهماته في الرياضيات.
كيف يتم الحصول على هذه القيمة؟
في الواقع، هناك عدة طرق لحساب رقم أويلر. ومع ذلك، تجدر الإشارة إلى أن أياً من الطريقتين لا تعطي نتيجة دقيقة. ولذلك فإن ترقيمها مستمر ولا نهائي، لكنه لا يتكرر.
في الواقع، في الوقت الحاضر، من المعروف أن أكثر من تريليون رقم يشكل الرقم e. المتسلسلة اللانهائية التي تحدد رقم أويلر هي:

ذهب “!” مضروب، والذي يتم تعريفه على أنه حاصل ضرب جميع الأعداد الطبيعية حتى هذا العدد. على سبيل المثال:
5! = 5 4 3 2 1 = 120
يمكننا أن نرى هذه المتسلسلة بيانياً كمجموع سلسلة من المستطيلات ذات الارتفاع 1 والعرض المتناقص، حيث عرض كل مستطيل هو 1/n!، حيث n هو عدد المضروب.
إذا قمنا بزيادة عدد المستطيلات في المجموع، فإن تقريب المساحة تحت منحنى الدالة الأسية يقترب أكثر فأكثر من رقم أويلر.
باختصار، رقم أويلر هو رقم ينتج عن مجموع سلسلة لا نهائية وهو أساسي في العديد من مجالات الرياضيات. على الرغم من أنه رقم غير نسبي ، إلا أن قيمته التقريبية هي 2.71828.
من المهم أن نضع في اعتبارنا أن أويلر نفسه طبق هذه الطريقة لحساب e حتى 18 منزلة عشرية.
طريقة أخرى لحسابها:
يمكننا حساب القيمة التقريبية لرقم أويلر على خط باستخدام سلسلة من الحدود المحدودة . على سبيل المثال، إذا أخذنا السلسلة اللانهائية الأولى المحددة أعلاه:

يمكننا حساب القيمة التقريبية عن طريق إضافة الحدود الأولى من السلسلة. على سبيل المثال، إذا أضفنا الحدود الستة الأولى:
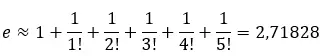
يمكننا رسم هذه المتسلسلة على خط لنرى كيف تقترب من القيمة التقريبية 2.71828 .
بيانياً، يمكن رسم الخط الذي يمثل رقم أويلر على شكل سلسلة من المستطيلات ارتفاعها 1 وعرضها متناقص، حيث عرض كل مستطيل هو 1/n!، حيث n هو عدد المضروب.
إذا قمنا بزيادة عدد المستطيلات في المجموع، فإن تقريب المساحة تحت منحنى الدالة الأسية يقترب أكثر فأكثر من رقم أويلر.
المعادلات الأسية مع رقم أويلر
يمكن استخدام المعادلات الأسية ذات رقم أويلر لنمذجة مجموعة واسعة من الظواهر في العلوم مثل الفيزياء وعلم الأحياء والاقتصاد وغيرها. وهنا بعض الأمثلة:
النمو الأسي والاضمحلال
يصف هذا النموذج المعدل الذي ينمو أو يتراجع فيه عدد السكان، أو المعدل الذي تتحلل به المادة السامة.
على سبيل المثال، إذا كان عدد السكان ينمو بمعدل 5٪ سنويًا، فيمكن وصف حجمه بالصيغة:
P(t) = P0 · e 0.05t حيث P0 هو الحجم الأولي للسكان.
نماذج الاضمحلال الإشعاعي
يصف هذا النموذج المعدل الذي تتحلل به الذرات المشعة مع مرور الوقت.
الصيغة هي كما يلي:
N(t) = N0 ه – lectt
حيث N0 هو العدد الأولي للذرات، و lect هو ثابت يعتمد على المادة المشعة و t هو الوقت.
هذه مجرد أمثلة قليلة لكيفية استخدام المعادلات الأسية مع رقم أويلر عمليًا. هناك العديد من المجالات الأخرى حيث تكون المعادلات الأسية مفيدة وذات صلة.
ما هي تطبيقات رقم أويلر؟
يحتوي رقم أويلر على مجموعة واسعة من التطبيقات في مجالات مختلفة من الرياضيات والعلوم. بعض الحقول التي يستخدم فيها الرقم e هي:
- الحساب والتحليل الرياضي : يستخدم في دراسة الدوال الأسية واللوغاريتمية، وفي حل المعادلات التفاضلية.
- نظرية الأعداد – تستخدم في دراسة توزيع الأعداد الأولية وفي حل المسائل المتعلقة بنظرية الأعداد.
- الاحتمالية والإحصاء : تستخدم في حل المسائل المتعلقة بتوزيع الاحتمالات وتقدير القيم المتوقعة.
- التشفير – يستخدم في دراسة خوارزميات التشفير وفك التشفير.
- الفيزياء – تستخدم لحل المشاكل المتعلقة بالديناميكا الحرارية وميكانيكا الكم والفيزياء الإحصائية.
- الكيمياء : تستخدم في حل المسائل المتعلقة بالديناميكا الحرارية الكيميائية والحركية الكيميائية.
صيغة أويلر للأعداد المركبة
تحدد صيغة أويلر للأعدادالمركبة علاقة بين الدوال المثلثية والأسية. الصيغة مكتوبة:

حيث أن “e” هو أساس اللوغاريتمات الطبيعية، و”i” هي الوحدة التخيلية، و”x” هو رقم حقيقي، و”cos” و”sin” هما الدوال المثلثية جيب التمام والجيب، على التوالي.
هذه الصيغة مفيدة جدًا في العديد من مجالات الرياضيات، بما في ذلك نظرية الأعداد ونظرية الوظائف ونظرية التعقيد، ولها مجموعة واسعة من التطبيقات في الهندسة والفيزياء والاقتصاد.
ومن الأمثلة العملية على استخدامه في تمثيل الإشارات والأنظمة في تحليل فورييه، حيث يتم تمثيل الإشارات الدورية كمجموع من الإشارات الجيبية المعقدة.
تُستخدم صيغة أويلر لوصف كيفية ارتباط هذه الإشارات المعقدة بالدوال المثلثية الفعلية التي تصف الإشارات الجيبية الفردية.
عدد أويلر والفائدة المركبة
الفائدة المركبة هي مفهوم مالي يصف العملية التي من خلالها يحصل مبلغ من المال، يسمى أصل الدين، على فائدة على الفائدة التي تزداد بمرور الوقت.
وبعبارة أخرى، فإن الفائدة المكتسبة من الاستثمار لا تأتي فقط من رأس المال الأولي، ولكن أيضًا من الفائدة المكتسبة في الفترات السابقة.
يرتبط رقم أويلر والفائدة المركبة لأن صيغة حساب الفائدة المركبة تستخدم رقم أويلر. صيغة الفائدة المركبة هي:
أ = ف ه ر
حيث A هو المبلغ النهائي، P هو رأس المال، r هو سعر الفائدة، t هو الوقت وe هو رقم أويلر. بهذه الطريقة، يعد رقم أويلر عاملاً مهمًا في الصيغة الرياضية لحساب الفائدة المركبة.
مثال على حساب الفائدة المركبة بأرقام محددة سيكون:
لنفترض أن لدينا استثمار بقيمة 1000 يورو بمعدل فائدة 5٪ سنويًا لمدة عامين. ستكون صيغة حساب الفائدة المركبة هي:
A = P e rt = 1000 e 0.05 2 = 1000 1.1025 = 1102.5 يورو.
وهذا يعني أنه بعد عامين، سيزيد رأس مالنا الأولي البالغ 1000 يورو إلى 1102.5 يورو بفضل الفائدة المركبة الناتجة.
أمثلة على التمارين الرياضية برقم أويلر
فيما يلي مثالان للمسائل الرياضية التي تم حلها والتي تتضمن رقم أويلر:
1. أوجد قيمة “e ix ” حيث x عدد حقيقي:
تخبرنا هوية أويلر أن e ix = cos(x) + i · sin(x). لذلك، إذا عرفنا قيمة x، فيمكننا حساب قيمة e ix باستخدام الدوال المثلثية.
2. احسب e^(x 2 ) لقيمة x معينة:
يمكننا استخدام متسلسلة تايلور لحساب قيمة e^(x 2 ). متسلسلة تايلور لـ e x هي توسعة لا نهائية تجعل من الممكن حساب تقديرات تقريبية متتالية لقيمة e x ، اعتمادًا على المصطلح المستخدم.

إذا استبدلنا x 2 بـ x في هذه المتسلسلة، فسنحصل على متسلسلة تايلور لـ e^(x 2 ).