الكسور أو الأعداد الكسرية هي مفهوم رياضي مهم جدًا في مجال حساب التفاضل والتكامل. لذلك، من الضروري معرفة كيفية عملها وكيفية حل تمارين الكسور . هذا هو الهدف من هذه المقالة، سواء تعلمت كيفية حل العمليات بالكسور وأي نوع آخر من التمارين أو المسائل التي تتضمن أرقامًا من هذا النمط. ومع ذلك، لنبدأ بالتمارين الأولى.
تمرين على العمليات على الكسور
للبدء، نقدم بعض العمليات الأساسية التي تتضمن الكسور، كل ما عليك فعله هو حلها والتعبير عن النتيجة المبسطة. لذلك، بمجرد الانتهاء من حل العمليات الحسابية ، ننصحك بمقارنة النتائج وإلقاء نظرة على التصحيح الذي نقدمه لك. على الرغم من أنه يمكنك أيضًا التحقق من نتائجك باستخدام حاسبة الكسور الموجودة على الإنترنت.
جمع وطرح الكسور ذات المقام المشترك
أدناه لديك جمع وطرح اثنين من الكسور التي تم حلها، حاول حلها بنفسك ومقارنة النتيجة. وبهذه الطريقة ستستعرض آليات الحل لهذا النوع من العمليات:
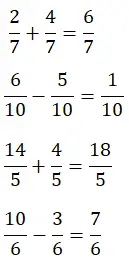
جمع وطرح الكسور ذات المقامات المختلفة
الآن نرفع المستوى قليلًا، لأنه لحل عملية جمع وطرح الكسور ذات المقامات المختلفة، نحتاج أولًا إلى إيجاد lcm للمقامات. وبالتالي يصبح الحساب أكثر تعقيدًا بعض الشيء.
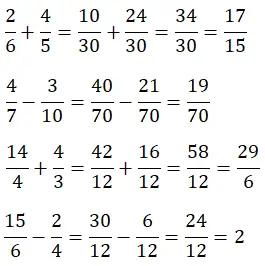
ضرب وقسمة الكسور
في هذا القسم، سيتعين عليك حل عمليات ضرب وقسمة الكسور، وهذه العمليات سهلة جدًا، لكنك لا تزال بحاجة إلى التدرب عليها. كما في القسمين السابقين، لديك اثنان من كل نوع.
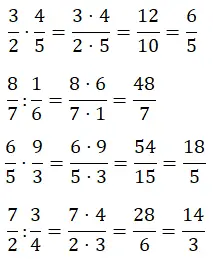
الكسور مجتمعة
أخيرًا، سيتعين عليك حل الكسور المجمعة ، وهي عمليات دمج الكسور. العنصر الأكثر تعقيدًا في هذه الأمور هو الحساب، حيث يتعين عليك جمع كل معرفتك حول العمليات باستخدام الأعداد الكسرية لتتمكن من حل عملية حسابية من هذا النوع بشكل صحيح.

تمرين في التحويل بين الكسور العشرية والكسور
يجب عليك الآن محاولة تحويل الأرقام العشرية التالية إلى كسر مولد والعكس صحيح. على الرغم من أنه للقيام بذلك بشكل صحيح، يجب عليك مراعاة نوع العلامة العشرية (دقيقة أو دورية خالصة أو دورية مختلطة) نظرًا لاختلاف طرق التحويل. إذا كنت لا تتذكر هذه الطرق، ننصحك بقراءة مقالنا عنالكسور ، لأننا نشرح فيه جميع إجراءات التحويل بين الكسور العشرية والكسور والعكس. يمكنك العثور أدناه على بعض التحويلات التي تم حلها، ونوصيك بمحاولة القيام بها بنفسك:

تمرين على الكسور المتكافئة
بعد التدرب على العمليات الحسابية والتحويلات الأساسية ، حان الوقت للبدء بالكسور المتكافئة . سنعرض لك في هذا القسم العديد من الكسور وستحتاج إلى العثور على أزواج الكسور المتكافئة. بهذه الطريقة ستتدرب على مفهوم التكافؤ وستراجع أيضًا تبسيط الكسور .

تمرين مقارنة الكسور
بعد ذلك، سنعرض لك عدة كسور وسيتعين عليك مقارنتها بالرموز “<“، “=” و “>”. لحل هذا التمرين، ستحتاج إلى إيجاد مقام مشترك وتحويل الكسرين إلى ذلك المقام. بهذه الطريقة ستتمكن من معرفة أي البسطين أكبر، وعليك التصرف وفقًا لذلك:

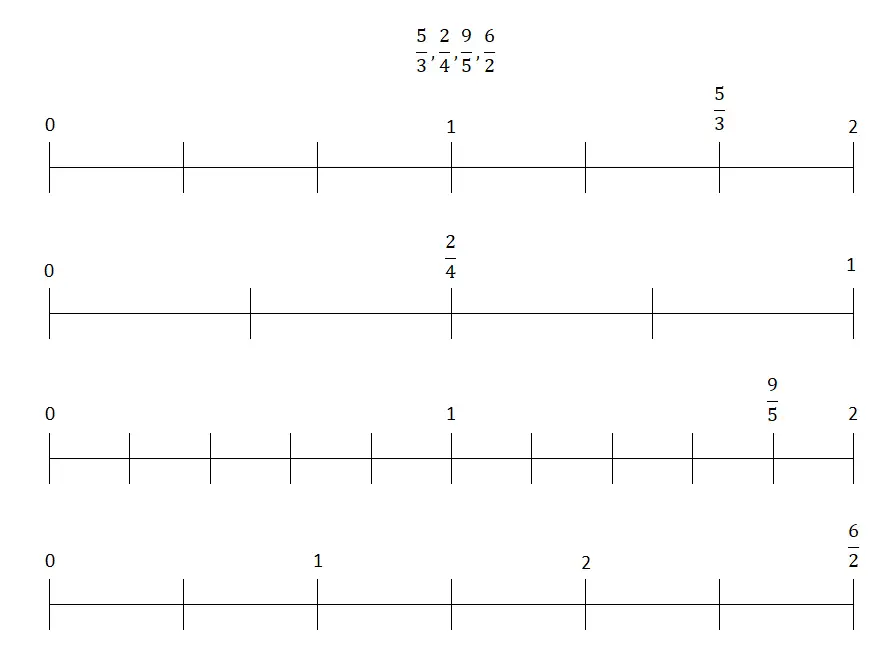
تمرين على الكسور على خط الأعداد
في هذا التمرين، سيتعين عليك ترتيب الكسور المختلفة التي سنقدمها لك علىخط الأعداد ، وبالتالي يمكن أن تكون إجراءات الحل متنوعة تمامًا. على سبيل المثال، يمكنك تقسيم المسافة بين رقمين صحيحين على عدد الأجزاء التي تشير إليها قيمة المقام، ثم ضع الكسر في القطعة التي يشير إليها البسط .
بالإضافة إلى ذلك، يمكنك قسمة البسط على المقام والحصول على رقم عشري، والذي ستضعه لاحقًا على السطر. على الرغم من أن هذا الإجراء الثاني هو أكثر أساسية ، ولهذا السبب اخترنا اختيار الطريقة الأولى التي شرحناها. ومع ذلك، فإن الكسور التي ستحتاج إلى وضعها على اليمين هي كما يلي:
مشاكل الكسر
وأخيرًا، نصل إلى الجزء الأخير من هذه المقالة، والذي سنتناول فيه بعض المسائل المتعلقة بالكسور. على الرغم من أننا نريد أولاً وصف الإجراء الصحيح الذي يجب عليك استخدامه عند حل المشكلات الرياضية :
- فهم المشكلة: الخطوة الأولى هي القيام بقراءة جيدة، تفهم من خلالها المشكلة بأكملها. بهذه الطريقة سوف تتعرف على كافة المعلومات الموضحة في الإعلان. إذا قمت بهذا الجزء بشكل صحيح، فقد أنجزت الكثير، لأنك ستعرف كيفية توجيه الحل وجميع الحسابات.
- بيان المشكلة: بمجرد أن تعرف ما هي المشكلة، سوف تحتاج إلى تقديمها. يمكنك القيام بذلك باستخدام مخطط أو رسم أو تمثيل رسومي صغير للبيانات. في هذه الخطوة، ستبدأ بالتفكير في طرق ربط البيانات وحل المشكلة.
- حل المشكلة نفسها: لاحقًا يمكنك الاستمرار في حل المشكلة عدديًا، في هذه المرحلة تحتاج إلى اختبار النظريات التي أثرتها في القسم السابق. هذا هو المكان الذي تقوم فيه بالفعل بتنفيذ خطة العمل والحصول على النتائج، لذلك عليك أن تكون شديد التركيز.
- تفسير الحلول: أخيرًا، عندما يكون لديك الحلول بالفعل، ستحتاج إلى تفسير هذه النتائج وفهمها في سياق المشكلة. هذه الخطوة الأخيرة مهمة جدًا ويتجاهلها الكثير من الناس، لأنهم يعتقدون أن النتيجة العددية كافية، لكن في الواقع عليك تلخيص الحل في جملة واحدة.
مشكلة 1
إذا أردنا ملء حوض سباحة بنقرة واحدة، فسيستغرق الأمر 6 ساعات، ولكن إذا فعلنا ذلك بنقرة أخرى، فسيستغرق الأمر 8 ساعات. ما هو المقدار الذي سيتم ملؤه من حوض السباحة خلال ساعتين إذا استخدمنا الصنبورين في نفس الوقت؟ التعبير عن النتيجة في صورة كسر.
لحل هذه المشكلة، علينا استخدام الكسور. ما سنفعله بشكل أساسي هو حساب المقدار الذي سيمتلئ به كل صنبور خلال هاتين الساعتين بشكل منفصل. لذا، فإن الصنبور الأول سوف يملأ 1/6 الخزان في ساعة واحدة، وإذا ضربناه في ساعتين، فسوف يملأ 2/6. بينما النقرة الثانية سوف تملأ 1/8 في الساعة وسيتعين علينا أيضًا ضربها في 2، والتي سيكون لدينا بها 2/8.
وأخيرًا، سنضيف الكسرين للحصول على المبلغ الإجمالي للمجمع الذي سيتم ملؤه. إذن يتبقى لدينا 2/6 + 2/8 = 7/12 من المجموعة.
مشكلة 2
لدينا 64 قطعة حلوى، لكننا نعطي ربعها لصديقنا ماركوس. ثم نأكل 3 قطع حلوى ونعطي 2/5 الكمية المتبقية لصديقتنا ماريا. كم تبقى لدينا من الحلوى؟ التعبير عنه كعدد صحيح.
نحتاج أولاً إلى طرح ربع من إجمالي المبلغ 64، ثم سنطرح 3 من النتيجة التي تم الحصول عليها وأخيراً سنطرح خمسي هذه الكمية من الحلوى. والتي يمكننا من خلالها حساب ذلك باستخدام الكسور المجمعة:
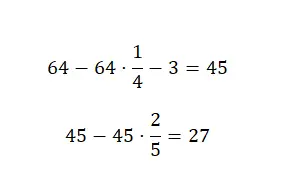
وبالتالي، في النهاية يتبقى لدينا 27 قطعة حلوى.
مشكلة 3
لدينا قطعة أرض مساحتها 10000 متر مربع مقسمة إلى ثلاثة أجزاء غير متساوية. القسم الأول يمثل 3/6 المساحة الكلية والقسم الثاني يساوي نصف القسم السابق. ما الكسر الذي يصف مساحة القسم الثالث؟ ما هو عدد الأمتار المربعة التي يمتلكها كل قطاع؟
أول شيء سنفعله هو حساب كسر المخطط الثالث، وسنفعل ذلك عن طريق طرح بسيط جدًا للكسور. بعد ذلك، سوف نقوم بحساب مساحة كل قسم عن طريق حساب الكسر من رقم، في حالتنا هذه القيمة العددية ستكون 10000. أدناه يمكنك رؤية الإجراء بأكمله: