الكسور أو الأعداد الكسرية هي تعبيرات عددية تشير إلى كمية مقسومة على كمية أخرى. وبالتالي فهي قيمة ممثلة بحاصل رقمين. مع هذا النوع من الأرقام يمكننا التعبير عن الكميات العشرية والأعداد الصحيحة ويمكننا حتى الإشارة إلى النسب . بعد ذلك، سنحدد الكسور بطريقة رياضية أكثر ونعرض لك بعض الأمثلة، حتى تتمكن من فهم هذا المفهوم بيانيًا.
ما هي الكسور؟
الكسر يساوي عدد الأجزاء التي نأخذها من الوحدة المقسمة إلى أجزاء متساوية. ومن ثم، يتم تمثيله بيانيًا بحدين يفصل بينهما خط أفقي في المنتصف. بتعبير أدق، في الجزء العلوي من السطر نجد البسط وتحت المقام.
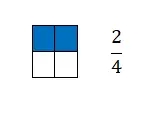
كما ترون، الكسور هي مفهوم رياضي سهل جدًا للرسم البياني لأنها تسير جنبًا إلى جنب مع النسب. ولهذا السبب قمنا في المثال السابق بالتعبير عن عدد المربعات الملونة بعدد كسري.
مصطلحات كسرية
جزأين من الكسر هما:
- البسط: يقع هذا الحد فوق الخط الأفقي وهنا نكتب عدد القطع التي نأخذها. يمكننا إيجاد البسط الموجب والسالب والصفر (يساوي الصفر).
- المقام: هذا المصطلح الآخر يقع أسفل الخط وهنا نكتب إجمالي عدد الأجزاء التي تنقسم إليها الوحدة. يمكننا إيجاد المقامات الموجبة والسالبة، لكن لا يمكن أن تكون صفرًا.
أنواع الكسور
هناك أنواع عديدة من الكسور، اعتمادًا على الأعداد التي تتكون منها ومدى تكافؤها مع الكسور الأخرى. بعد ذلك، سنحدد جميع الفئات الموجودة وسنعلق على الخصائص التي تسمح لها بالتمييز عن غيرها:
- الكسور الصحيحة: هي تلك التي يكون بسطها أقل من مقامها. إذا قمت بتحويل هذه الكسور إلى عدد عشري ، فستحصل على رقم بين صفر وواحد. ولا يمكن أن يكون أكبر من واحد، لأن قيمة البسط ستكون دائمًا أقل من قيمة المقام، وبالتالي لن يتم تجاوز الوحدة.
- الكسور غير الحقيقية: هي تلك التي يكون بسطها أكبر من مقامها، وهي في هذه الحالة تعبر عن قيم عددية أكبر من الوحدة. على سبيل المثال، 8/5 يساوي 1.6 وهو أكبر من 1. وهذه طريقة أخرى للتعبير عن الأعداد الكسرية، وهي النوع التالي.
- الكسور المختلطة: وتسمى أيضًا الأعداد الكسرية، وهي تلك التي تتكون من عدد صحيح وعدد مختلط. يتم تمثيلها بشكل أساسي بقيمة عددية قبل الكسر، لذا لتحويلها إلى كسور غير حقيقية تحتاج إلى ضرب الجزء الصحيح في المقام وإضافته إلى البسط وترك المقام كما هو.
- الكسور العشرية: هي تلك التي لها مقام يعبر عن كمية تعادل قوة العشرة، على سبيل المثال: 6/10، 34/1000، أو 5/100. يتم استخدامها في التدوين العشري وهي الأكثر شيوعًا عند تحويل الأرقام العشرية الدقيقة إلى أرقام مختلطة. سنناقش هذا بمزيد من التفصيل في القسم التالي.
- الكسور المركبة: هي التي تتكون من كسر آخر، إما في البسط، أو في المقام، أو في كليهما. إذن، لتبسيط هذه التعبيرات وإظهارها ككسر واحد، علينا قسمة البسط على المقام. وسيصبح هذا أكثر وضوحًا عندما نشرح التقسيم بين الكسور.
- الكسور المتكافئة: هي تلك التي تعادل نفس العدد، رغم أنها لا تتكون من نفس البسط أو المقام. على سبيل المثال، 8/4 = 4/2 = 2، كلا الكسرين يساوي اثنين. في هذه الحالة تحديدًا، يرجع ذلك إلى أن الكسر الأول يساوي ضعف الكسر الثاني، وبالتالي فإنه يحافظ على علاقة تناسب.
- الكسور غير القابلة للاختزال: هي تلك التي لا يمكن تبسيطها أكثر، لأن البسط والمقام لا يشتركان في عوامل مشتركة، وبالتالي لا يمكن قسمتهما على أي رقم. بعض الأمثلة على هذا النوع هي: 9/5، 5/6، 7/8 وغيرها. لمعرفة كيفية اكتشافها، من المهم معرفة كيفية حساب القاسم المشترك الأكبر .
العمليات مع الكسور
الآن بعد أن عرفنا الفئات المختلفة للكسور الموجودة، سنرى كيفية حل العمليات الحسابية المختلفة باستخدام الأعداد الكسرية . تجدر الإشارة إلى أن هذا الأمر أكثر تعقيدًا بعض الشيء من العمليات التي تتم على الأعداد الصحيحة، على الرغم من أنه بمجرد فهم المنهجية، يصبح كل شيء سهلاً للغاية. علاوة على ذلك، لن نقوم بشرح النظرية فحسب، بل سنعرض لك أيضًا بعض الأمثلة. ومع ذلك، فلنبدأ.
مجموع الكسور
تعد إضافة الكسور ذات المقام المشترك أمرًا بسيطًا للغاية، حيث أنك تقوم فقط بإضافة البسطين وتترك المقام كما هو. من ناحية أخرى، فإن جمع الكسور ذات المقامات المختلفة يصبح أمرًا صعبًا بعض الشيء، لأنه يتعين عليك إيجاد المضاعف المشترك الأصغر للمقامات. وبعد ذلك، يجب علينا جمع حاصل ضرب كل بسط عن طريق قسمة lcm (المقام الجديد) على المقام القديم. لفهم أفضل، يمكنك إلقاء نظرة على الرسم البياني التالي:
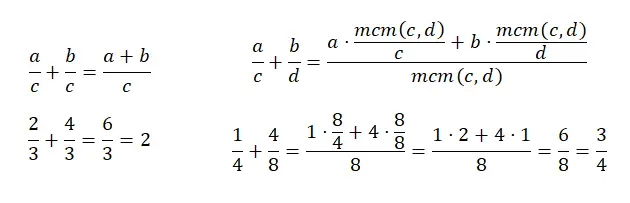
كسور الطرح
طرح الكسور ذات المقام المشترك يشبه إلى حد كبير عملية الجمع، في الواقع كل شيء يتم بنفس الطريقة باستثناء مجموع البسطين، لأنه بدلاً من الجمع، عليك الطرح. وفي طرح الكسور ذات المقامات المختلفة، يحدث نفس الشيء، إنه نفس الشيء تقريبًا باستثناء أنه بدلاً من إضافة منتج البسط بقسمة lcm على المقام القديم، يجب علينا طرح . هنا رسم تخطيطي آخر:
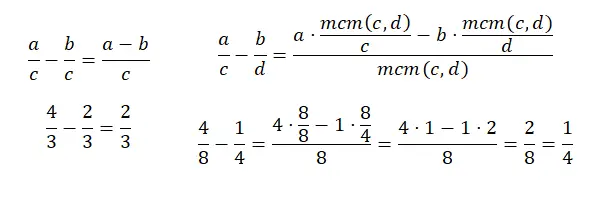
مضاعفة الكسور
يمكن حل ضرب الكسور بنفس الطريقة سواء كانت المقامات واحدة أم لا. في الأساس، عليك ضرب البسط في جزء واحد والمقامات في جزء آخر. ربما تكون هذه هي أبسط عملية، حيث أنك تحتاج فقط إلى إجراء ضربتين.
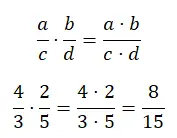
تقسيم الكسور
من السهل أيضًا حل التقسيم إلى كسور ، ما عليك سوى ضرب الصلبان. بمعنى آخر، البسط هو نتيجة ضرب بسط الكسر الأول في مقام الثاني. حيث أن المقام هو حاصل ضرب مقام الكسر الأول وبسط الثاني.
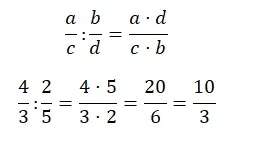
تبسيط الكسور
تبسيط الكسور أو تقليل الكسور ليس عملية حسابية في حد ذاتها، ولكن من المهم جدًا معرفة كيفية القيام بذلك، وهو أيضًا موضوع تناولناه بالفعل قليلًا مع أنواع الكسور. إذن، لتبسيط عدد كسري، علينا قسمة البسط والمقام على العدد نفسه. وبشكل عام، سنختار العامل المشترك الأكبر لإجراء هذا التبسيط. في الصورة التالية يمكنك العثور على مثال.
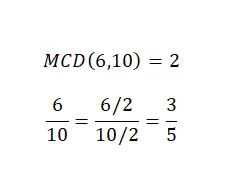
كما ترون، لدينا كسرين متكافئين ، لذا فإن كلاهما يمثل نفس القيمة العددية، ولكن الثاني أبسط من الأول. ولذلك، فقد نجحنا في تحقيق هدف التبسيط.
كيفية الانتقال من العدد العشري إلى الكسر والعكس؟
الكسر المولد هو الكسر غير القابل للاختزال الذي يتم الحصول عليه من رقم عشري، إما رقم عشري دقيق أو رقم عشري متكرر. بالطبع، سنحتاج إلى استخدام طرق مختلفة اعتمادًا على نوع العلامة العشرية، وهو ما سنناقشه أدناه.
تحويل من العشري الدقيق لتوليد الكسر
وفي هذه الحالة يمكننا اللجوء إلى الكسور العشرية التي علقنا عليها في البداية. ببساطة، علينا كتابة القيمة العددية في البسط، ولكن بدون العلامة العشرية. بينما نكتب في المقام قوة العشرة التي تحتوي على عدد من الأصفار يساوي عدد الأرقام في البسط.
ومع ذلك، إذا كان لدينا عدد عشري أكبر من واحد، مثل 4.25، فسنحتاج إلى ضرب عدد الوحدات الكاملة التي لدينا في قيمة المقام وإضافتها إلى البسط الأصلي. ستجد أدناه مثالاً لكل نوع:
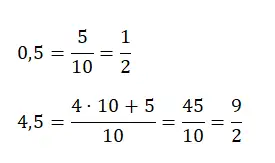
تحويل العشري المتكرر النقي إلى توليد الكسر
عندما يكون لدينا رقم عشري دوري خالص ، إذا أردنا الحصول على الكسر المولد، فسيتعين علينا وضع نفس القيمة في البسط، ولكن بدون علامة عشرية وطرح الجزء الصحيح. في حين أن المقام سيكون مساويًا لرقم يتكون من تسعة فقط، إلا أنه يجب علينا على وجه التحديد أن نكتب عددًا من التسعات يساوي عدد الأرقام في الجزء العشري من الرقم الأصلي. هذا النظام محير إلى حد ما، لكن مع بعض الأمثلة سنفهمه:
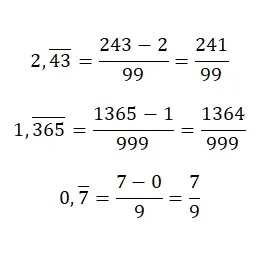
تحويل الكسور العشرية المتكررة المختلطة إلى توليد الكسور
في حالة وجود رقم عشري مختلط متكرر ، سيتعين علينا تطبيق قاعدة معقدة إلى حد ما. أولاً، سنكتب الرقم بدون الفاصلة في البسط ونطرح الجزء الصحيح متبوعًا بالكسور العشرية غير المتكررة، بدون الفاصلة أيضًا. أما بالنسبة للمقام، فسوف تحتاج إلى كتابة عدد من التسعات يساوي عدد الأرقام في الجزء العشري الدوري، متبوعة بعدد من الأصفار يساوي عدد الأرقام في الجزء العشري غير المتكرر.
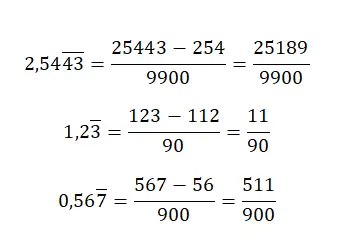
تحويل الكسر إلى عشري
للانتقال من كسر إلى عدد عشري، ما عليك سوى قسمة البسط على المقام، لأن الرقم المختلط ليس أكثر من حاصل قسمة بين قيمتين . لذلك، من خلال حل القسمة، تحصل على الرقم العشري المقابل. في الصورة التالية يمكنك العثور على بعض الأمثلة البسيطة إلى حد ما:
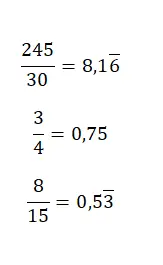
تمارين الكسور
الآن بعد أن عرفت كل النظريات المتعلقة بالكسور، ننصحك بممارسة بعض التمارين. بهذه الطريقة سوف تتعلم كل المفاهيم الموضحة بمزيد من التعمق وفي يوم الامتحان سوف تكون أسرع في حل العمليات الحسابية. بالإضافة إلى ذلك، ستكون قد شاهدت جميع أنواع تمارين الكسور الموجودة وستعرف كيفية حلها وفقًا لذلك. أخيرًا، دعني أخبرك أن لدينا أيضًا تحت تصرفك آلة حاسبة للكسور عبر الإنترنت، والتي يمكنك من خلالها حل جميع عمليات الكسور.