دالة متعددة الحدود

ستجد هنا ما هي الدوال متعددة الحدود وما هي جميع أنواع الدوال متعددة الحدود. بالإضافة إلى ذلك، سنشرح أيضًا خصائص الدوال متعددة الحدود.

ما هي وظيفة متعددة الحدود؟

دالة متعددة الحدود هي دالة تعبيرها الجبري هو متعدد الحدود ، أي أن دالة متعددة الحدود يتم تعريفها عن طريق إضافة أو طرح عدد محدود من الحدود ذات الدرجات المختلفة.

ولذلك، يتم وصف دالة متعددة الحدود رياضيا بالتعبير التالي:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

من ناحية أخرى، يمكن أيضًا تعريف الدوال متعددة الحدود باستخدام الصيغة التالية:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

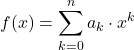
حيث الشروط

$a_k$

$x^k$

هما على التوالي معامل ومتغير كل وحدة واحدة تشكل دالة متعددة الحدود.

على المدى

$a_nx^n$

، المسمى بالمصطلح الرئيسي، يشير إلى درجة الدالة كثيرة الحدود، لأنها أعلى درجة أحادية الحد للدالة. بمعنى آخر، أكبر قيمة أسية هي التي تشير إلى درجة الدالة كثيرة الحدود.

على الرغم من أننا سنرى المزيد من خصائص الدوال كثيرة الحدود أدناه، إلا أن مجال أي دالة كثيرة الحدود هو جميع الأعداد الحقيقية.

أنواع الدوال متعددة الحدود

بالنظر إلى تعريف دالة كثيرة الحدود، سنرى الآن ما هي جميع أنواع الدوال متعددة الحدود الموجودة.

وظيفة ثابتة

الدالة الثابتة هي دالة متعددة الحدود من الدرجة 0، لذا فهي نوع من الوظائف التي تأخذ دائمًا نفس الصورة لأي قيمة للمتغير المستقل (x).

التعبير العام للدالة الثابتة هو كما يلي:

$f(x)=k$

على سبيل المثال، الدوال الثلاث التالية هي ثوابت أو دوال متعددة الحدود من الدرجة صفر:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

التمثيل الرسومي للدالة الثابتة هو خط أفقي (موازي للمحور السيني) بقيمة تساوي الثابت.

يمكنك رؤية المزيد من الميزات حول هذا النوع من الوظائف في الرابط التالي:

➤ انظر:خصائص الدالة الثابتة

دالة خطية

الدالة الخطية ، وتسمى أيضًا الدالة المتقاربة، هي دالة متعددة الحدود من الدرجة الأولى. وبالتالي، لا يمكن أن تتكون دالة متعددة الحدود من هذا النوع إلا من حد خطي وحد مستقل:

$f(x)=mx+n$

ذهب

$m$

هو ميل الخط و

$n$

هو التقاطع y، أي حيث تعبر الدالة المحور Y.

أمثلة على الدوال الخطية أو الدوال متعددة الحدود من الدرجة الأولى:

$f(x)=4x+3\qquad f(x)=-5x$

يميز البعض بين الوظيفة الخطية والوظيفة المتقاربة اعتمادًا على ما إذا كانت الوظيفة لها مصطلحها

$n$

أم لا، كونها الدالة المتقاربة مع التقاطع والدالة الخطية بدونها.

التمثيل الرسومي للوظائف الخطية هو دائمًا خطوط تعتمد درجة ميلها على قيمة ميل الوظيفة.

أدناه يمكنك رؤية دالة متعددة الحدود من الدرجة الأولى بيانياً

$f(x)=2x-1.$

ومع ذلك، لتمثيل دالة خطية، يجب أن تكون واضحًا بشأن عدة مفاهيم. ستجد في الرابط التالي شرحًا خطوة بخطوة لكيفية رسم دالة متعددة الحدود من هذا النوع رسمًا بيانيًا:

➤ انظر: التمثيل الرسومي للدالة الخطية

وظيفة من الدرجة الثانية

الدالة التربيعية هي دالة متعددة الحدود من الدرجة الثانية، أي دالة حدها الأعلى هو من الدرجة الثانية.

ولذلك، فإن صيغة الدالة التربيعية هي:

$f(x)=ax^2+bx+c$

ذهب

$ax^2$

هو الحد التربيعي,

$bx$

المصطلح الخطي و

$c$

الحد المستقل للدالة كثيرة الحدود.

أمثلة على الدوال التربيعية أو الدوال التربيعية متعددة الحدود:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

الرسم البياني للدالة التربيعية يكون دائمًا قطعًا مكافئًا ويعتمد شكله على إشارة المعامل الرئيسي.

$a:$

إذا كان المعامل
$a$

موجبة، والدالة التربيعية محدبة (على شكل

$\bm{\cup}$

).
بدلا من ذلك، إذا كان المعامل
$a$

سالبة، والدالة التربيعية مقعرة (على شكل

$\bm{\cap}$

).

لذا، باستخدام إشارة المعامل الرئيسي للدالة التربيعية كثيرة الحدود، يمكننا معرفة الشكل الذي سيتخذه الرسم البياني الخاص بها، ولكن لتمثيلها الرسومي الدقيق، يجب اتباع إجراء محدد. يمكنك رؤية هذا الإجراء في الرابط التالي:

➤ انظر: التمثيل الرسومي للدالة التربيعية

وظيفة مكعبة

الدالة التكعيبية هي دالة متعددة الحدود من الدرجة الثالثة. ولذلك، يتم التعبير عن هذا النوع من الدوال متعددة الحدود جبريا على النحو التالي:

$f(x)=ax^3+bx^2+cx+d$

أمثلة على الدوال التكعيبية أو الدوال متعددة الحدود من الدرجة الثالثة:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

تتوافق التمثيلات الرسومية للوظائف المكعبة مع المنحنيات المكعبة. ومع ذلك، لتمثيل هذا النوع من الوظائف في الرسم البياني، يجب اتباع إجراء معقد (يتضمن المشتقات). يمكنك أن ترى كيف يتم ذلك هنا:

➤ انظر: كيفية تمثيل دالة

كما ترون، فإن أنواع الدوال كثيرة الحدود هي في الواقع لا نهائية، حيث أن متعددة الحدود يمكن أن تحتوي على حدود لا نهائية. على سبيل المثال، الدالة من الدرجة الرابعة تشبه الدالة التكعيبية ولكن مع إضافة حد تربيعي. الشيء المهم هو أن تفهم أن نوع الدالة كثيرة الحدود يتحدد بدرجة الدالة.

خصائص وظائف متعددة الحدود

وظائف كثيرة الحدود لها الخصائص التالية:

مجال أي دالة متعددة الحدود هو مجموعة الأعداد الحقيقية.

$\text{Dom } f=\mathbbf{R}$

جميع الدوال متعددة الحدود مستمرة.

الدوال متعددة الحدود ذات الدرجة الأكبر من 1 ليس لها خطوط مقاربة.

بغض النظر عن نوع الدالة كثيرة الحدود، فإن نقطة التقاطع الوحيدة مع المحور الإحداثي (المحور Y) هي عند ارتفاع حدها المستقل، أي عند النقطة التالية:

$(0,a_0)$

من ناحية أخرى، فإن الدالة متعددة الحدود تعترض محور الإحداثي السيني (المحور X)، على الأكثر، بقدر عدد مرات درجة الدالة.

إذا كانت الدالة كثيرة الحدود لها حدود ذات درجة زوجية فقط، فهذا يعني أنها متناظرة حول محور OY. من ناحية أخرى، إذا كانت الدالة كثيرة الحدود تحتوي فقط على حدود ذات درجة فردية، فهذا يعني أن الدالة متماثلة حول أصل الإحداثيات.

عدد الحدود القصوى النسبية (الحد الأقصى أو الأدنى) للدالة كثيرة الحدود هو، على الأكثر، درجة كثير الحدود للدالة ناقص 1.

عدد نقاط انعطاف دالة كثيرة الحدود يساوي على الأكثر درجة كثير حدود الدالة ناقص 2.

يمكن إجراء العمليات باستخدام وظائف متعددة الحدود:
- مجموع دالتين متعددي الحدود يعطي دالة متعددة الحدود أخرى.
- ناتج ضرب دالتين كثيرتي الحدود يؤدي إلى ظهور دالة متعددة الحدود أخرى.
- يؤدي ضرب دالة كثيرة الحدود بعدد قياسي (رقم حقيقي) إلى الحصول على دالة متعددة الحدود مماثلة ولكن مع تقليل الرسم البياني الخاص بها أو توسيعه.
- إن تكوين دالتين متعددي الحدود يساوي دالة متعددة الحدود أخرى.