ربما سمعت عن الأعداد المركبة . ربما تكون هذه المجموعة من الأعداد هي الأصعب في التعامل معها، لأنها تجمع بين أرقام حقيقية وأرقام خيالية. وتوحيدها يجعل من الممكن دراسة السلوكيات العددية التي لا يمكن معالجتها باستخدام جميع الأعداد الحقيقية.
ما هي الأعداد المركبة؟
الأعداد المركبة هي مزيج من عدد حقيقي وعدد خيالي . على سبيل المثال، 4 + 5i هو عدد مركب جزءه الحقيقي يساوي 4 وجزء وهمي يساوي 5i. وبشكل عام يمكننا التعبير عنها بالصيغة التالية:
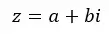
حيث Re(z) = a وIm(z) = b
وكما قلنا جيدًا، فإن المجمعات هي أكبر مجموعة أو مجموعة عالمية ، والتي تتضمن كلا من الأعداد الحقيقية والأعداد التخيلية. بعد ذلك، نعرض لك رسمًا تخطيطيًا صغيرًا للبنية الهرمية لجميع المجموعات:

ومن ثم، عندما يكون لدينا عدد حقيقي وعدد تخيلي، يكون لدينا عدد مركب. لكن هناك أوقات يكون فيها أحد الجزأين يساوي صفرًا. ماذا يحدث في هذه الحالات؟ حسنًا، ما زلنا نتعامل مع المجمعات، لأن المجموعة المعقدة تشمل جميع المجموعات العددية الأخرى. لكننا ندخل فئة فرعية مختلفة:
| عدد مركب | الحزب الملكي | جزء الخيال | تصنيف فرعي |
| 2+5ط | 2 | 5i | معقد |
| 4 | 4 | 0 | ملكي نقي |
| 3ط | 0 | 3ط | محض خيال |
عندما يكون لدينا حقيقي خالص، حيث أن القيمة التخيلية b تساوي صفرًا، فإن العدد المركب المتبقي يعادل:
ض = أ + 0i = أ
ومن ناحية أخرى، عندما يكون لدينا خيال محض، فإن a يساوي صفرًا، وبالتالي يبقى العدد المركب كما يلي:
ض = 0 + ثنائية = ثنائية
التمثيل البياني للأعداد المركبة
لتمثيل الأعداد المركبة، نستخدم المستوى المركب . والذي يتكون من خطين : الخط الحقيقي والخط التخيلي. يتم استخدام خطي الأعداد هذين لتحديد الأرقام في كل مجموعة بيانيًا وإذا جمعناها معًا نحصل على خطة، مثل:

يُسمى المحور X بالمحور الحقيقي لأنه يوجد فيه قيم الجزء الحقيقي. بينما يُسمى المحور Y بالمحور التخيلي، فهذا هو المكان الذي تُكتب فيه القيم التخيلية. دعونا نرى مثالاً، سنضع الرقم 3 + 2i في المستوى المركب.

كما رأيت في الصورة، قمنا بتحديد موقع الرقم باستخدام الرقمين 3 و2 كإحداثيات، كل منهما لمحور. إذا كنت تريد معرفة المزيد حول تمثيل الأعداد المركبة، ننصحك بقراءة هذه المقالة.
ما هي أنواع الأعداد المركبة؟
والآن سنرى الطرق التي يمكننا بها التعبير عن عدد مركب. حتى الآن لم نر سوى الصيغة الأساسية (التي تسمى الصيغة ذات الحدين)، والتي تكتب كمجموع: الجزء الحقيقي بالإضافة إلى الجزء التخيلي.
لكن، في الواقع، لدينا ثلاثة أشكال: ذات الحدين، والقطبية، والمثلثية . كل نوع من التعبير له خصائصه ويستخدم في موقف أو آخر. لذلك سنقوم بشرحها جميعًا وإظهار كيفية الانتقال من واحدة إلى أخرى.
1. شكل ذو الحدين
تتم كتابة الأعداد المركبة في صورة ذات الحدين كمجموع الجزء الحقيقي والجزء التخيلي: a + bi. على سبيل المثال، الرقم 6 + i هو رقم مركب يتم التعبير عنه بترميز ذي الحدين. في هذا، الصيغة هي نفسها دائمًا:

لذلك، للتعبير عن عدد مركب في صورة ذات الحدين، ما عليك سوى معرفة قيمته الحقيقية وقيمته التخيلية.
على سبيل المثال، القيمة 3 + 2i تكون في صيغة ذات الحدين، وكما رأينا سابقاً يتم تمثيلها على النحو التالي:

يستخدم النموذج ذو الحدين بشكل أساسي لحل عمليات جمع وطرح الأعداد المركبة.
2. الشكل القطبي
للتعبير عن الأعداد المركبة بالشكل القطبي ، يجب علينا حساب وحدتها |z| وحجته. تُستخدم الصيغة القطبية بشكل أساسي عندما نحتاج إلى حل عمليات ضرب وقسمة الأعداد المركبة.
لحساب معامل العدد المركب، ما عليك سوى حساب معامل a وb، كما هو موضح في الصيغة التالية:

ولحساب وسيطة أو زاوية z، نحتاج إلى حساب ظل الزاوية لـ b بين a:

من المهم ملاحظة أنه لتحديد قيمة الزاوية α بدقة، من الضروري تحديد الربع الذي تقع فيه. في الواقع، تحسب دالة الظل القوسي الزوايا الواقعة بين π/2 و-π/2 فقط. لتحديد الربع الذي يقع فيه العدد المركب، يجب أن ننظر إلى القيمتين a وb (إذا كانت موجبة أو سالبة):
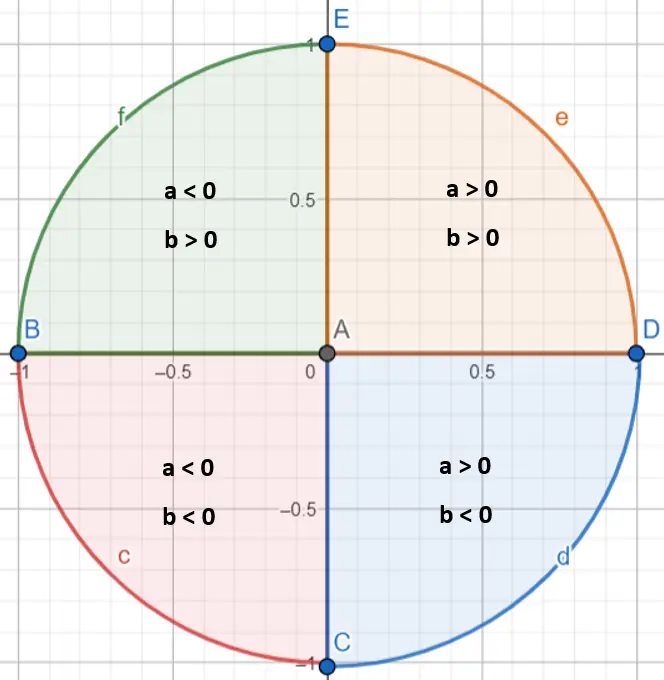
بمجرد أن نعرف الربع الذي يقع فيه رقمنا، نحتاج إلى اتباع بعض القواعد:
- إذا كان العدد المركب موجودًا في الربع الأول (a > 0 وb > 0)، فسنترك الوسيطة كما هي.
- إذا كان العدد المركب موجودًا في الربع الثاني (a < 0 و b > 0)، فسنضيف π إلى الوسيطة.
- إذا كان العدد المركب يقع في الربع الثالث (a < 0 و b < 0)، فإننا نطرح π من الوسيطة.
- إذا كان العدد المركب موجودًا في الربع الرابع (a > 0 وb <0)، فسنضيف 2π إلى الوسيطة.
في حال كنت لا تعرف ما الذي نتحدث عنه عندما نقول الربع، ننصحك بمراجعة مقالتنا حول النسب المثلثية .
بمجرد أن نعرف مقدار وسعة z، يمكننا التعبير عن العدد المركب في الصورة القطبية. على الرغم من أن هذا النموذج يقبل عدة تسميات، إلا أن التسميتين الرئيسيتين هما:

على سبيل المثال، إذا أردنا تغيير الرقم 3 + 5i إلى رقم قطبي، فنحن ببساطة بحاجة إلى اتباع الإجراء التالي.
نحسب الوحدة أولاً:
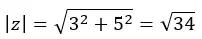
ثم نحسب السعة الموجودة في الربع الأول، فتظل كما حسبناها.
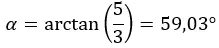
ونعبر عن العدد بالصورة القطبية:
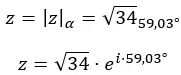
تمثيلها الرسومي هو كما يلي:
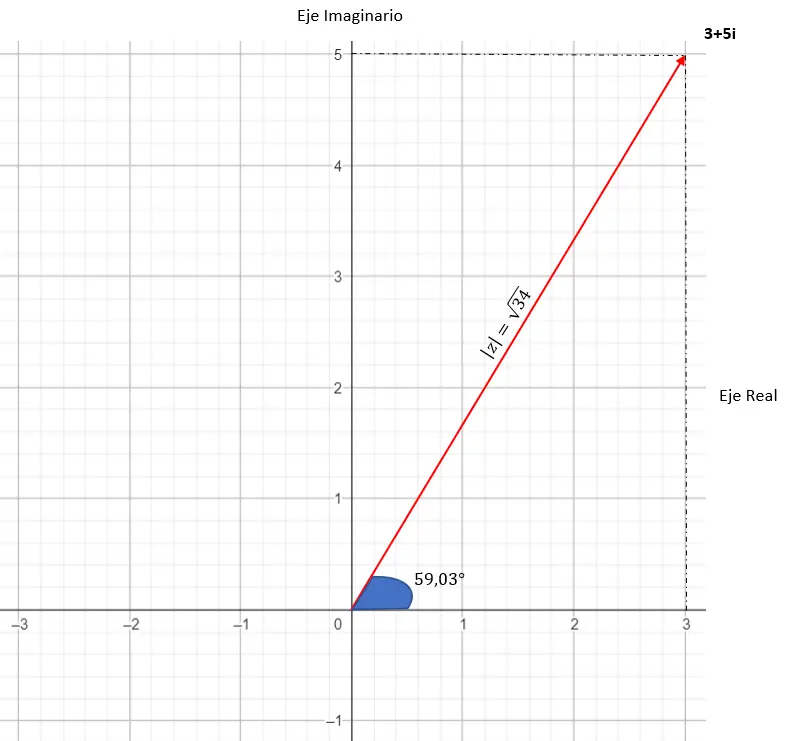
3. الشكل المثلثي
أخيرًا، لدينا الترميز المثلثي ، والذي يتم حسابه منصيغة أويلر :

على سبيل المثال، للتعبير عن العدد 4 – 3i بالشكل المثلثي، نتبع الإجراء التالي:
نبدأ بحساب المقياس والسعة باستخدام الصيغ التي استخدمناها في قسم الصورة القطبية.
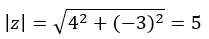
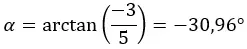
تنبيه: الوسيطة موجودة في الربع الرابع، لأن (a > 0 وb <0).
نضيف البيانات إلى المعادلة في شكل مثلثي.
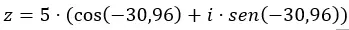
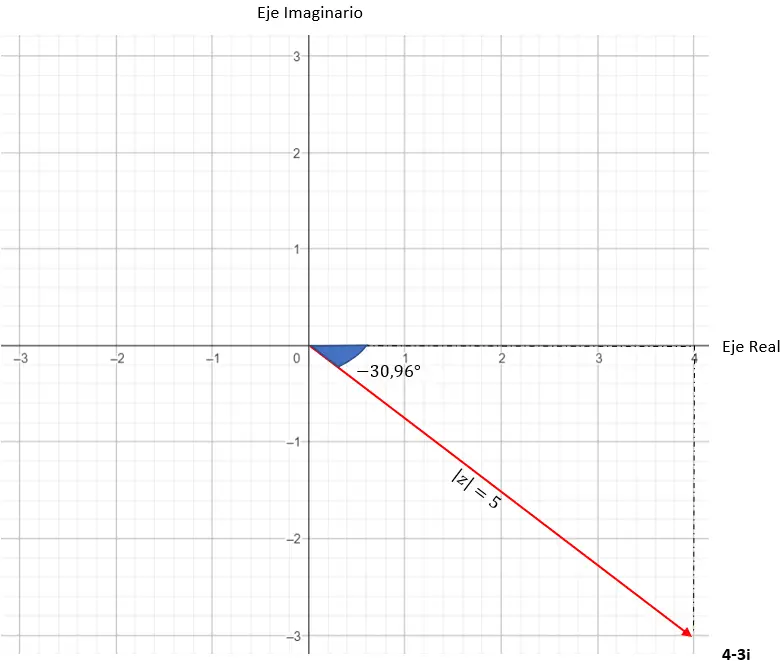
ولدينا بالفعل العدد المعبر عنه بالصورة المثلثية. تمثيلها الرسومي هو على النحو التالي.
كيفية التبديل من نوع إلى آخر؟
أنت الآن تعرف كل الطرق للتعبير عن عدد مركب. وخلال القسم الأخير، تمكنت من رؤية كيفية الوصول إلى كل واحد منهم، ولكن قبل أن ننتهي نريد أن نقدم ملخصًا سريعًا لكيفية الانتقال من نموذج إلى آخر. ما عليك سوى استخدام الصيغ التي رأيناها في القسم السابق.
من الشكل ذي الحدين إلى الشكل القطبي والعكس
للانتقال من ذات الحدين إلى القطبية، نقترح الرسم البياني التالي:
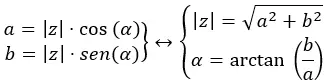
لقد رأينا مثالاً سابقًا حيث انتقلنا من ذات الحدين إلى القطبية، لذا سننتقل الآن من القطبية إلى ذات الحدين باستخدام الرسم البياني أعلاه. علينا تحويل √41 38.66 إلى ذات الحدين.
نقوم أولا بحساب أ.
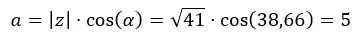
ثم نحسب ب.
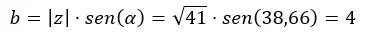
ونعبر عنها بصيغة ذات الحدين.
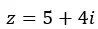
يبدو التمثيل الرسومي لهذا الرقم كما يلي:
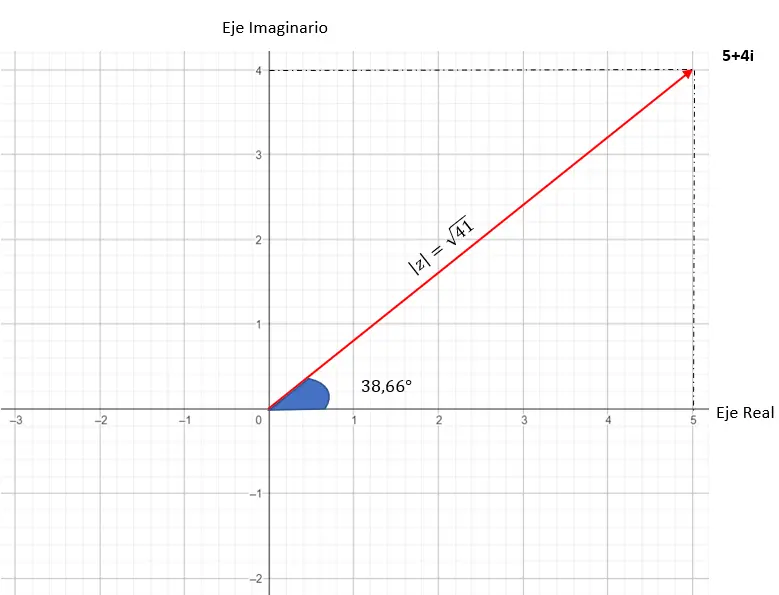
من الشكل ذي الحدين إلى الشكل المثلثي والعكس
للانتقال من ذات الحدين إلى المثلثية، عليك أيضًا تطبيق الصيغ التي تحدثنا عنها في القسم السابق. بهذه الطريقة، نحسب أولًا المقياس والسعة، ثم نضع هذه البيانات في معادلة الصورة المثلثية. على سبيل المثال، سنمرر الرقم z = 3 + 2i بشكل مثلثي.
نحسب أولاً المعامل والوسيطة.
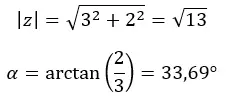
تنبيه: الوسيطة موجودة في الربع الأول، لأن (a > 0 و b > 0).
ثم نكمل المعادلة المثلثية بهذه البيانات.
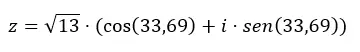
وإذا أردنا الانتقال من المثلثية إلى ذات الحدين، فكل ما علينا فعله هو حل التعبير السابق.
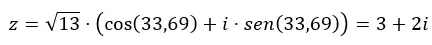
من الشكل القطبي إلى الشكل المثلثي والعكس
وأخيرًا، سننتقل من الصورة القطبية إلى الصورة المثلثية. وهو أمر بسيط للغاية، لأنه يتم التعبير عن هذين النموذجين بنفس القيمتين: modulo وargument . لذلك تحتاج فقط إلى ملء النماذج وهذا كل شيء.
لنعطي مثالاً، سنقوم بتحويل الرقم z = √85 12.53 إلى صيغة مثلثية.
نعيد صياغة المتغيرين (الوحدة النمطية والوسيطة) في معادلة الصورة المثلثية:
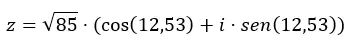
والآن بعد أن عرفت كيفية الانتقال من شكل إلى آخر، ننصحك بالتدرب قليلًا مع بعض التمارين . بهذه الطريقة سوف تقوم بتوحيد المعرفة التي تعلمتها في هذه المقالة. إذا كان لديك أي أسئلة بخصوص هذا الموضوع فلا تتردد في تركها في التعليقات. وإذا كنت تريد معرفة المزيد عن الأعداد المركبة، فراجع الروابط أدناه.
مزيد من المعلومات حول الأعداد المركبة
- أرقام خيالية
- خصائص الأعداد المركبة
- العمليات على الأعداد المركبة
- جذور الأعداد المركبة
- التمثيل البياني للأعداد المركبة