Angle entre une droite et un plan

Vous trouverez ici comment l’angle entre une droite et un plan est calculé. Vous pourrez également voir des exemples et, en plus, vous entraîner avec des exercices résolus pas à pas d’angles entre des lignes et des plans.

Quel est l’angle entre une droite et un plan ?

L’angle entre une droite et un plan est l’angle entre la droite et sa projection orthogonale sur le plan.

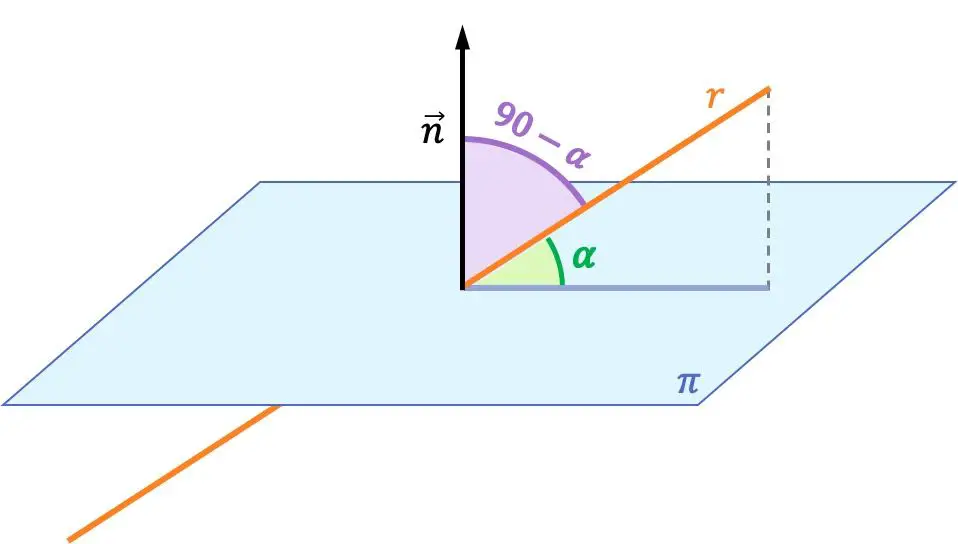
L’angle entre une droite et un plan est le complément de l’angle entre ladite droite et le vecteur normal au plan. Par conséquent, l’angle entre une droite et un plan est calculé à partir de l’angle entre le vecteur directeur de la droite et le vecteur normal du plan.

Formule d’angle entre une droite et un plan

Pour déduire la formule de l’angle entre un plan et une droite, il faut savoir trouver l’angle entre deux vecteurs . Sur la page liée, vous trouverez l’explication ainsi que des exemples et des exercices résolus étape par étape, donc si vous ne vous souvenez pas comment le faire, nous vous recommandons de jeter un coup d’œil.

Ainsi, puisque l’angle entre une droite et un plan est complémentaire de l’angle entre le vecteur directeur de ladite droite

$(\vv{\text{v}}_r)$ et le vecteur normal audit plan $(\vv{n})$ , de la formule de l’angle entre deux vecteurs on déduit que l’angle entre une droite et un plan est équivalent à l’expression suivante :

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Par conséquent, la formule de l’angle entre une droite et un plan est la suivante :

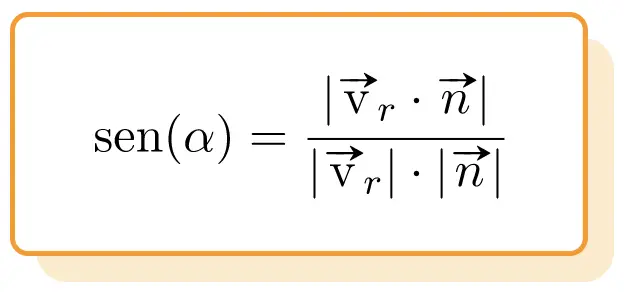
angle entre une droite et un plan formule

Où:

$\vv{\text{v}}_r$ est le vecteur direct de la droite.
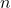$\vv{n}$ est le vecteur normal au plan.

Exemple de calcul de l’angle entre une droite et un plan

Afin que vous puissiez voir comment résoudre ce type de problème, voici un exemple de calcul de l’angle entre une droite et un plan :

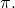Calculer l’angle formé par la droite $r$ avec l’avion $\pi.$ Soit leurs équations :

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

La ligne est exprimée sous forme d’équations paramétriques, donc son vecteur directeur est :

$\vv{\text{v}}_r = (-1,4,-3)$

D’autre part, le plan est défini sous la forme d’une équation implicite (ou générale), donc son vecteur normal est :

$\vv{n} = (1,-1,4)$

Ainsi, une fois que l’on connaît le vecteur directeur de la droite et le vecteur normal du plan, on applique la formule de l’angle entre une droite et un plan :

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

On substitue les vecteurs dans la formule :

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

Et on fait les calculs :

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Enfin, on inverse le sinus avec la calculatrice et on trouve la valeur de l’angle :

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

L’angle entre la ligne et le plan est donc d’environ 51,80º.

Il faut tenir compte du fait que si jamais nous obtenons un résultat de 0º, cela signifie que la droite et le plan sont parallèles ou que la droite est contenue dans le plan. Et si l’angle est égal à 90º, cela implique que la ligne et le plan sont perpendiculaires.

Problèmes résolus de l’angle entre une droite et un plan

Exercice 1

Trouver l’angle formé par la droite

$r$ avec l’avion $\pi.$ Soit leurs équations :

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

voir solution

La droite est exprimée sous la forme d’une équation continue, donc son vecteur directeur est :

$\vv{\text{v}}_r = (2,-1,-3)$

D’autre part, le plan est sous la forme d’une équation implicite (ou générale), donc son vecteur normal est :

$\vv{n} = (3,1,2)$

Ainsi, une fois que nous connaissons le vecteur directeur de la droite et le vecteur normal du plan, nous utilisons la formule de l’angle entre une droite et un plan :

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Enfin, nous inversons le sinus et trouvons la valeur de l’angle :

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Par conséquent, l’angle entre la ligne et le plan est de 4,10º.

Exercice 2

Déterminer l’angle formé par la droite

$r$ avec l’avion $\pi.$ Soit leurs équations :

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

voir solution

La droite est exprimée avec ses équations implicites (ou générales), il faut donc trouver le vecteur directeur de la droite en calculant le produit vectoriel des vecteurs normaux aux 2 plans qui déterminent la droite :

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

D’autre part, le vecteur normal au plan est :

$\vv{n} = (-4,2,0)$

Ainsi, une fois que nous connaissons le vecteur directeur de la droite et le vecteur normal du plan, nous utilisons la formule de l’angle entre une droite et un plan :

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Enfin, nous inversons le sinus et trouvons la valeur de l’angle :

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Par conséquent, l’angle entre la ligne et le plan est de 46,33º.

Exercice 3

Trouver, à l’aide de la formule de l’angle entre une droite et un plan, la valeur de

$k$ nécessaire pour le droit $r$ et l’avion $\pi$ être parallèle.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

voir solution

Tout d’abord, la ligne est exprimée sous la forme d’une équation vectorielle, donc son vecteur directeur est :

$\vv{\text{v}}_r = (4,-1,3)$

D’autre part, le plan est sous la forme d’une équation générale, donc son vecteur normal est :

$\vv{n} = (4,3,k)$

Ainsi, pour que les deux éléments géométriques soient parallèles, l’angle entre eux doit être nul. Par conséquent, la formule de l’angle entre une droite et un plan est la suivante :

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Ainsi, le produit scalaire entre le vecteur directeur de la ligne et le vecteur normal doit être nul. Et à partir de cette équation, nous pouvons déterminer la valeur de l’inconnue

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Enfin, si vous avez trouvé cet article utile, vous êtes probablement également intéressé par la façon de trouver l’ angle entre deux plans . Sur la page de liens, vous trouverez une explication très détaillée ainsi que la formule nécessaire pour calculer l’angle entre deux plans différents et, en plus, vous pourrez voir des exemples et des exercices résolus étape par étape pour pouvoir pratiquer et comprendre comment cela se fait parfaitement.

Quel est l’angle entre une droite et un plan ?

Formule d’angle entre une droite et un plan

Exemple de calcul de l’angle entre une droite et un plan

Problèmes résolus de l’angle entre une droite et un plan

Exercice 1

Exercice 2

Exercice 3

Leave a Comment Cancel Reply