Angle entre deux droites (formule)

Sur cette page, vous trouverez l’explication de la façon de calculer l’angle entre deux lignes (formule). Vous pourrez également voir plusieurs exemples et, en plus, vous pourrez vous entraîner avec des exercices résolus étape par étape.

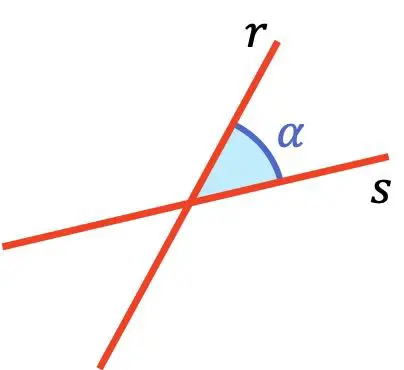
Quel est l’angle entre deux droites ?

L’angle entre deux lignes est le plus petit angle entre ces deux lignes.

Dans le plan, il existe quatre types de lignes en fonction de l’angle qu’elles forment entre elles : les lignes qui se croisent (entre 0º et 90º), les lignes perpendiculaires (90º), les lignes parallèles (0º) et les lignes coïncidentes (0º).

lignes sécantes

Les lignes sécantes se croisent en formant un angle aigu entre 0º et 90º.

Lignes droites perpendiculaires

angle entre deux droites perpendiculaires

Les lignes perpendiculaires se coupent avec un angle droit de 90º.

Lignes parallèles

Les lignes parallèles ne se touchent jamais et font un angle de 0º entre elles.

lignes coïncidentes

Deux lignes coïncidentes ont tous des points en commun et, par conséquent, il y a toujours un angle de 0º entre elles.

En conclusion, le calcul de l’angle entre deux droites parallèles, coïncidentes ou perpendiculaires est immédiat : les droites parallèles et les droites coïncidentes forment un angle de 0 degré puisqu’elles ont la même direction, et les droites perpendiculaires se coupent avec un angle de 90 degrés. Par contre, pour trouver l’angle entre deux droites sécantes, il faut appliquer une formule (on le verra plus bas).

Comment est calculé l’angle entre deux droites ?

Il existe deux façons de calculer l’angle entre deux droites. La première méthode utilise le vecteur directeur de chaque ligne et la seconde méthode est basée sur la pente de chaque ligne.

Aucune procédure n’est meilleure que l’autre, en fait les deux sont assez faciles, mais selon la manière dont les lignes sont exprimées, une méthode ou une autre est pratique. Nous vous recommandons donc de savoir utiliser les deux méthodes mathématiques.

Méthode d’orientation des vecteurs de lignes

La formule pour calculer l’angle entre deux droites à l’aide de leurs vecteurs directeurs est la suivante :

Étant donné les vecteurs directeurs de deux lignes différentes :

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

L’angle entre ces deux lignes peut être calculé avec la formule suivante :

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Où

$\lvert \vv{\text{u}} \rvert$ et $\lvert \vv{\text{v}} \rvert$ sont les modules des vecteurs $\vv{\text{u}}$ et $\vv{\text{v}}$ respectivement.

N’oubliez pas que la formule de la magnitude d’un vecteur est :

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Voyons comment trouver l’angle entre deux lignes avec un exemple :

Calculez l’angle entre les deux droites suivantes :

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Pour calculer l’angle entre les deux droites, il faut d’abord trouver le vecteur directeur de chaque droite.

le droit

$r$ s’exprime sous la forme d’ une équation paramétrique , donc les composantes du vecteur qui marque sa direction sont :

$\vv{r} = (-3,4)$

et le droit

$\displaystyle s$ est défini sous la forme d’une équation implicite (ou générale), donc les coordonnées de son vecteur directeur sont :

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Maintenant que nous connaissons le vecteur directeur de chaque droite, nous pouvons utiliser la formule de l’angle entre deux droites :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Nous déterminons donc la magnitude des deux vecteurs :

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Nous effectuons les opérations vectorielles de la formule d’angle :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

Et, enfin, on calcule l’angle formé par les deux droites avec l’inverse du cosinus :

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

N’oubliez pas que vous pouvez calculer l’inverse du cosinus à l’aide de la calculatrice avec la touche

$\boxed{\cos ^{-1}}.$

méthode de la pente

Évidemment, pour comprendre cette méthode, vous devez connaître la pente de la droite . Vous pouvez revoir ce concept dans le lien, où vous trouverez une explication détaillée de ce que cela signifie, comment il est calculé, des exemples et des exercices résolus de la pente d’une ligne.

La formule pour calculer l’angle entre deux droites à partir de leurs pentes est la suivante :

Soit deux lignes distinctes :

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

L’angle entre ces deux lignes peut être déterminé avec la formule suivante :

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Où

$m_1$ et $m_2$ sont les pentes des droites $r_1$ et $r_2$ respectivement.

Voyons comment calculer l’angle entre deux lignes en utilisant leurs pentes avec un exemple :

Trouvez l’angle entre les deux droites suivantes :

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

La pente de chaque ligne est le nombre avant la variable

$x:$

$m_r = 4$

$m_s = -3$

Par conséquent, l’angle entre les deux lignes peut être trouvé en appliquant la formule de pente :

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

Et enfin on trouve l’angle avec l’inverse de la tangente :

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

N’oubliez pas que vous pouvez calculer l’inverse de la tangente à l’aide de la calculatrice avec la touche

$\boxed{\tan ^{-1}}.$

Nous venons de voir un exemple avec les pentes de deux droites exprimées sous la forme d’une équation explicite, mais si elles étaient sous la forme d’une équation de pente ponctuelle, cette même procédure devrait être utilisée.

Résolution des problèmes d’angles entre deux lignes

Exercice 1

Déterminer l’angle formé par les deux droites suivantes :

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

voir solution

Dans ce cas, nous utiliserons la méthode des vecteurs directeurs. par conséquent, nous devons d’abord trouver le vecteur directeur de chaque ligne. Les deux lignes sont exprimées sous la forme d’équations paramétriques, de sorte que les composantes de leurs vecteurs directeurs sont les termes devant le paramètre

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Maintenant que nous connaissons le vecteur directeur de chaque droite, nous pouvons utiliser la formule de l’angle entre deux droites :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Nous déterminons donc la magnitude des deux vecteurs :

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

On résout le produit scalaire entre les deux vecteurs du numérateur et la multiplication des modules du dénominateur :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

Et, pour finir, on trouve l’angle formé par les deux droites en faisant l’inverse du cosinus :

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Exercice 2

Trouvez l’angle entre les deux droites suivantes :

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

voir solution

Nous allons résoudre ce problème en utilisant la méthode du vecteur de direction, nous devons donc d’abord trouver le vecteur de direction de chaque ligne. le droit

$r$ s’exprime sous la forme d’une équation générale (ou implicite), telle que les composantes du vecteur qui marque sa direction soient :

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

et le droit

$\displaystyle s$ est défini sous la forme d’une équation continue, donc les coordonnées cartésiennes de son vecteur directeur sont les nombres des dénominateurs :

$\vv{s} = (6,3)$

Une fois que nous connaissons le vecteur directeur de chaque droite, nous pouvons utiliser la formule de l’angle entre deux droites :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

On détermine donc les modules des deux vecteurs :

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

On fait les opérations entre vecteurs de la formule d’angle :

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

Et, enfin, on calcule l’angle formé par les deux droites avec l’inverse du cosinus :

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Exercice 3

Quel est l’angle entre les deux droites suivantes ?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

voir solution

Dans ce cas, nous utiliserons la méthode des pentes des lignes pour connaître l’angle qu’elles font, puisque les lignes sont sous la forme d’une équation explicite.

La pente de chaque ligne est le nombre qui accompagne la variable indépendante

$x:$

$m_r = -2$

$m_s = 5$

Par conséquent, l’angle entre les deux lignes peut être déterminé en appliquant la formule de pente :

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

Et enfin on trouve l’angle entre les deux droites en inversant la tangente :

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Exercice 4

Trouver l’équation de la droite qui passe par le point

$P(5,-1)$ et fait un angle de 45º avec la ligne $r.$ Être dit ligne:

$\displaystyle r: \ y=2x+4$

voir solution

Pour résoudre le problème, nous appellerons

$s$ à la droite que nous allons calculer. De plus, nous utiliserons la méthode de la pente car nous connaissons la pente de la droite $r:$

$m_r=2$

A partir de la formule de l’angle entre deux droites (méthode des pentes) on peut obtenir la valeur de la pente de la droite

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Nous substituons les valeurs connues dans la formule:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

Et nous essayons de résoudre l’équation résultante :

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

La valeur absolue de l’équation la rend quelque peu difficile à résoudre, car il faut analyser à la fois l’option positive et l’option négative :

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Nous avons donc deux solutions possibles : une droite de pente -3 et une autre droite de pente un tiers.

La formule de l’équation point-pente d’une droite est :

$y-y_0=m(x-x_0)$

Par conséquent, une fois que nous connaissons la pente des deux lignes possibles, nous pouvons écrire l’équation point-pente de chaque ligne avec le point par lequel elles doivent passer selon l’énoncé,

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Quel est l’angle entre deux droites ?

Comment est calculé l’angle entre deux droites ?

Méthode d’orientation des vecteurs de lignes

méthode de la pente

Résolution des problèmes d’angles entre deux lignes

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply