Comment factoriser des polynômes

Qu’est-ce que la factorisation des polynômes ? C’est une technique mathématique qui permet de décomposer un polynôme en facteurs ou expressions plus simples. Et grâce à cette simplification, nous pourrons effectuer des opérations entre plusieurs expressions algébriques plus facilement et confortablement. Ainsi, tout au long de cet article, nous aborderons différentes méthodes de factorisation des polynômes et tous les cas possibles de factorisation.

Comment factoriser un polynôme ?

Il existe de nombreuses méthodes de factorisation qui ont leur propre structure de résolution, mais qui finalement reposent sur la même chose. De plus, vous pouvez également trouver une grande variété de cas concernant la configuration du polynôme. C’est pourquoi dans les sections suivantes, nous discuterons de toutes les procédures qui existent et quand utiliser chacune d’elles. Enfin, nous l’appliquerons à un exemple réel afin que vous finissiez d’acquérir les concepts.

Factoriser un polynôme avec la règle de Ruffini

La méthode la plus utilisée pour factoriser les polynômes est la règle de Ruffini , car elle est facile à utiliser et le résultat peut être trouvé rapidement. La chose normale est d’utiliser cette technique pour factoriser des polynômes de degré supérieur à deux, voire parfois pour factoriser des polynômes du second degré. Puisqu’il vous permet d’obtenir les racines de ce polynôme très graphiquement. Bien que cette utilisation sera expliquée dans la section suivante qui se concentre sur les racines d’une expression mathématique de ce type.

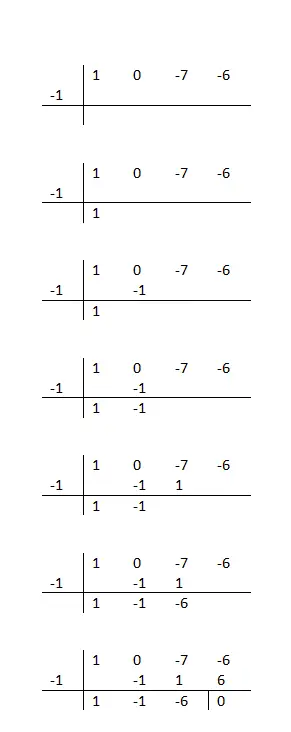
Comment faire Ruffini pour factoriser des polynômes ?

Fondamentalement, nous devrons écrire les coefficients du dividende dans une ligne horizontale et la valeur d’une éventuelle racine du polynôme dans le côté. On dit possible, car il va falloir chercher un diviseur qui permette d’obtenir un reste égal à zéro. Sinon, ce nombre ne sera pas une racine valide et vous devrez continuer à essayer.

Comme astuce, nous vous recommandons d’essayer uniquement les nombres diviseurs du terme indépendant (dernière valeur de la ligne horizontale). Ainsi, pour savoir si le nombre que vous avez choisi est correct, il vous suffit de suivre la séquence de calculs suivante :

Vous diminuez le coefficient, le multipliez par la racine que vous testez, l’écrivez sous le coefficient suivant et effectuez une addition verticale. Vous n’aurez qu’à répéter ces étapes jusqu’à la fin, et une fois que vous aurez terminé, vous saurez si cette valeur est correcte ou non. Puisque seuls les nombres qui donnent un reste nul seront valides.

Si la procédure mathématique que vous devez suivre n’est pas très claire pour vous, vous pouvez regarder l’exemple dans la colonne à gauche de ce texte. Aussi, nous vous recommandons d’essayer de factoriser le polynôme suivant : x³ + 2x² – x – 2 (basé sur l’exemple). Et enfin, pour savoir si vous avez correctement ou non résolu l’exercice, vous pouvez comparer votre résultat avec celui-ci :

Expression excédentaire = x² + 3x + 2
reste = 0

Nous allons maintenant faire une brève explication sur l’ application de Ruffini dans la factorisation . Bien que si vous voulez savoir comment cette ressource mathématique est utilisée en détail, nous vous recommandons d’accéder au dernier article que nous avons lié, car tout y est très bien expliqué. Cela dit, commençons par expliquer comment factoriser les polynômes avec la règle de Ruffini :

Nous dessinons la grille : comme on peut le voir sur l’image ci-dessus, nous allons créer une boîte dans laquelle nous ferons le Ruffini. En gros, il faut écrire les coefficients de l’expression ordonnés horizontalement et sans laisser ceux qui ont une valeur nulle. Au final, vous devriez avoir une représentation similaire à celle de l’image mais avec les valeurs de votre polynôme.
Nous calculons les racines : une fois que nous avons dessiné la structure et que nous nous sommes assurés que tous les nombres sont correctement écrits, nous procéderons au calcul de la racine. Vous devrez trouver les racines en suivant la séquence de calcul dont nous avons parlé juste au-dessus de cette liste (avec les images).
On exprime la racine sous la forme (x – a) : quand on a toutes les racines du polynôme alors on doit les exprimer sous la forme suivante (x – a). En tenant compte du fait que a sont les valeurs que nous avons obtenues, par exemple si nous avons extrait comme résultat x = 2, x = -2 et x = 4, alors nous obtiendrons (x – 2), (x + 2) et (x – 4).
Nous rassemblons tous les facteurs dans une seule expression : enfin, quand nous aurons déjà toutes les racines exprimées dans le bon format, il nous suffira de les rassembler dans une seule expression algébrique. En continuant avec l’exemple précédent, nous aurions quelque chose comme ceci : (x – 2) · (x + 2) · (x – 4).

Factoriser un polynôme en utilisant les racines d’un polynôme

Nous avons à moitié expliqué le concept racine d’un polynôme dans la section de Ruffini. Mais, la définition exacte serait : la racine d’un polynôme P(x) est une valeur numérique a, telle que P(a) = 0 . C’est donc un nombre capable d’annuler la fonction ou le polynôme en question. En résumé, on pourrait dire qu’il est utilisé pour décomposer un polynôme en produit de facteurs.

Par exemple, si on nous donne l’expression suivante x² − x − 2 et que nous la factorisons soit en utilisant la règle de Ruffini, soit en résolvant simplement l’équation quadratique x² − x − 2 = 0. Nous obtiendrons deux valeurs x = -1 et x = 2, donc si nous les changeons au format (x – a) et les mettons ensemble, nous arriverons à l’expression suivante : (x + 1) (x − 2), c’est-à-dire le polynôme factorisé . Et nous pouvons appliquer cela aux polynômes de degré supérieur à deux, bien que l’expression soit composée de plusieurs termes.

Factorisation d’un polynôme par extraction de facteur commun

Lorsque nous voulons factoriser des polynômes sans terme indépendant ou des expressions qui ont un facteur commun à tous les termes, nous pouvons alors simplifier le polynôme au moyen de cette technique. Il consiste essentiellement à appliquer la propriété distributive à l’expression entière, en supprimant ce facteur commun qui se répète et en l’ajoutant en multipliant le polynôme entier. Vous trouverez ci-dessous un exemple du premier cas dont nous avons parlé (polynôme sans terme indépendant) :

2x³ + 10x² – 6x = 2x (x² + 5x – 3)

Double extraction du facteur commun

L’extraction des facteurs communs peut même être effectuée en extrayant des facteurs plus complexes, qui incluent plusieurs variables. Et vous pouvez même extraire des polynômes dérivés de l’expression principale elle-même. Il est important de ne pas se fixer de limites lorsque l’on souhaite effectuer ce type d’opération, car l’objectif de l’extraction de facteurs est de simplifier au maximum une expression algébrique .

Factorisation de polynômes à l’aide d’identités notables

Des produits notables peuvent nous aider à factoriser des expressions polynomiales, puisqu’il s’agit en quelque sorte d’expressions algébriques simplifiées. Ils nous aident donc à passer directement d’un long polynôme à une petite formule composée de quelques termes. Il est donc fortement recommandé d’apprendre les formules des identités notables pour pouvoir identifier rapidement quand on peut les utiliser. Et par conséquent, nous faire gagner du temps d’affacturage avec Ruffini ou l’une des autres méthodes. Ensuite, nous aborderons les trois règles que vous devez apprendre :

Différence des carrés : a² – b² = (a + b) · (a – b)
Carré de la somme : a² + 2ab + b² = (a + b)²
Carré de soustraction : a² – 2ab + b² = (a – b)²

Factorisation de polynômes par regroupement

Dans quelques cas on peut trouver un polynôme de structure x² – ax – bx + ab , qui peut être simplifié en retirant un facteur commun : x (x – a) – b (x – a). Et si nous reprenons le facteur commun, il peut encore être simplifié : (x – a) · (x – b). Par conséquent, les racines de ce polynôme seraient x = a et x = b. Comme vous pouvez le voir, ce type d’expression algébrique a une structure très facile à factoriser et à utiliser.

Exercices de factorisation polynomiale

Enfin, nous souhaitons vous proposer une série d’exercices afin que vous puissiez vous exercer à factoriser des polynômes. De cette façon, vous pourrez mieux intérioriser la théorie que nous avons expliquée aujourd’hui. Simplement, vous devez résoudre les exercices de votre cahier puis comparer les résultats avec ceux que nous vous proposons ci-dessous.

x ⁴ -1 = (x ² + 1) (x + 1) (x – 1)
x ⁵ + x ⁴ – x – 1 = (x – 1) (x + 1) ² (x ² + 1)
^9×2 + 30x + 25 = (3x + 5) ²
x ⁴ – 3x ³ – 3x ² + 11x – 6 = (x + 2) (x – 3) (x – 1) ²