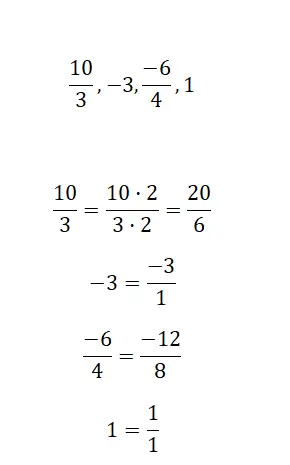Dans cet article, vous trouverez une explication sur les fractions équivalentes ou les fractions égales qui est très complète et facile à comprendre. Plus précisément, nous parlerons de leur définition, comment les calculer et comment savoir si deux fractions sont équivalentes. De cette façon, vous finirez par savoir tout ce dont vous avez besoin pour résoudre des exercices sur des fractions équivalentes comme ceux que nous vous présenterons à la fin. Cela dit, commençons par le sujet.
Calculateur de fractions équivalentes
Avec l’aide de ce calculateur de fractions équivalentes, vous pourrez vérifier si deux fractions sont égales, sans avoir besoin de faire des calculs. Son fonctionnement est très simple, en gros, vous devez entrer les valeurs correspondant aux deux numérateurs et aux deux dénominateurs et appuyer sur le bouton “Calculer”.
Que sont les fractions équivalentes ?
Les fractions équivalentes sont celles qui expriment la même valeur numérique , par conséquent, ce sont des fractions qui sont équivalentes au même résultat, même si elles ont un numérateur et un dénominateur différents. Cela signifie qu’ils entretiennent une relation proportionnelle, qui peut être de deux types : amplifiée ou simplifiée. Ensuite, nous vous montrons un exemple graphique de fractions équivalentes afin que le concept soit mieux compris.
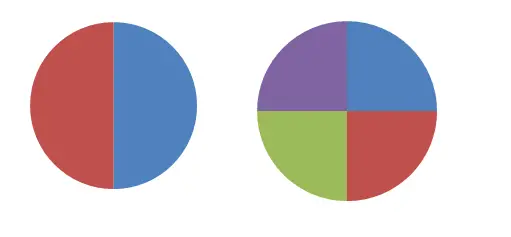
Dans l’image précédente, vous pouvez voir deux cercles divisés en deux et quatre parties. Si nous essayons de définir le premier par une fraction, nous dirons que chaque partie est égale à 1/2 du tout, tandis que dans le second chiffre nous utiliserons la fraction 1/4. Évidemment, ces deux fractions ne sont pas équivalentes , puisqu’elles représentent des quantités différentes. Mais, si l’on prend deux morceaux du deuxième cercle (2/4), cette expression équivaut à 1/2.
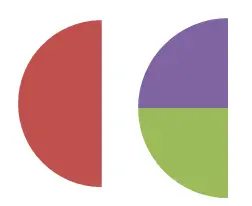
Dans cette deuxième image, vous pouvez voir l’ équivalence entre 1/2 et 2/4 , également, elle peut être vérifiée numériquement. Puisque 1/2 = 0,5 et 2/4 = 0,5. Selon la définition que nous avons commentée précédemment, si les deux fractions expriment la même valeur numérique, alors ce sont des fractions équivalentes.
Exemples de fractions équivalentes
Nous allons maintenant vous montrer 5 exemples de fractions équivalentes. Et si vous voulez comprendre comment nous les avons calculés, nous vous recommandons de continuer à lire.
- Fractions équivalentes à un demi : 2/4, 3/6, 4/8, etc.
- Fractions équivalentes à un tiers : 2/6, 3/9, 4/12, etc.
- Fractions équivalentes à un quart : 2/8, 3/12, 4/16, etc.
- Fractions égales à l’unité : 4/4, 7/7, 15/15, etc.
- Fractions équivalentes à un quinte : 2/10, 3/15, 4/20, etc.
Comment calculer des fractions équivalentes ?
Pour obtenir des fractions équivalentes, nous devons multiplier ou diviser le numérateur et le dénominateur par le même nombre. Puisque, si nous modifions les deux parties de la fraction de la même manière, nous maintenons une relation proportionnelle. Par conséquent, nous pouvons utiliser deux méthodes : l’amplification et la réduction.
Trouver une fraction équivalente par amplification
Dans ce premier cas, nous devons multiplier une fraction initiale par une certaine valeur numérique. Cela signifie que nous devons multiplier le numérateur et le dénominateur par ce nombre. Pour que vous puissiez le voir avec un exemple, nous vous montrons ci-dessous deux fractions équivalentes, qui sont obtenues après avoir fait une multiplication :
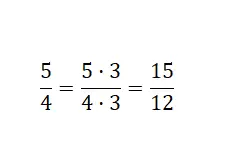
Ce que nous avons fait est de multiplier les deux parties de la fraction par trois : 5 x 3 = 15 et 4 x 3 = 12 . On obtient ainsi une fraction équivalente amplifiée, puisqu’elle est plus grande. En conclusion, nous avons trouvé une fraction composée de différentes valeurs numériques, qui exprime la même quantité que la fraction originale.
Trouver une fraction équivalente par simplification
Deuxièmement, nous pouvons choisir desimplifier une fraction en divisant le numérateur et le dénominateur d’une fraction donnée. De cette façon, nous obtiendrons une autre fraction équivalente , encore plus simple que la première. Cependant, il convient de mentionner que cette méthode ne fonctionne que si l’expression initiale n’est pas une fraction irréductible , car cette dernière ne peut pas être réduite davantage. Vous trouverez ci-dessous un exemple de calcul d’une fraction équivalente par réduction (simplification).
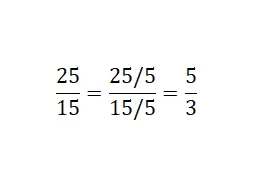
Comme vous pouvez le voir sur l’image, ce que nous avons fait est de diviser à la fois le numérateur et le dénominateur de la fraction par un diviseur commun . Dans cet exemple, nous en avons utilisé cinq : 25/5 = 5 et 15/5 = 3. Enfin, nous avons obtenu la fraction équivalente irréductible de 25/15.
Comment savoir si deux fractions sont équivalentes ?
Pour identifier les fractions équivalentes, nous devons suivre l’une des trois procédures que nous expliquerons ci-dessous. Il convient de noter que la seconde est liée à la simplification des fractions dont nous avons parlé dans la section précédente.
Multiplication des numérateurs par les dénominateurs
Si vous voulez vérifier l’équivalence entre deux fractions, vous pouvez utiliser cette première procédure. En gros, il faut multiplier le numérateur de la première fraction par le dénominateur de la seconde. Ensuite, vous devez multiplier le numérateur de la deuxième fraction par le dénominateur de la première. Si les deux résultats vous donnent le même , alors ces fractions seront équivalentes. Regardez l’exemple suivant :
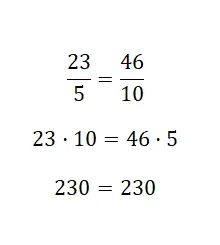
Dans ce dernier exemple, nous avons vérifié que les deux fractions étaient équivalentes. Cet exemple était facile à voir, puisque la deuxième fraction est le double de la première, c’est-à-dire qu’elles ont une relation d’équivalence amplifiée . Il convient de noter que cette procédure est assez confortable à utiliser, il suffit simplement de multiplier les croix. Mais nous vous recommandons également d’apprendre à utiliser les deux autres systèmes, car vous aurez ainsi plus de ressources mathématiques à votre disposition.
Simplifier des fractions
Lorsqu’il s’agit de fractions non irréductibles , on peut utiliser cette autre méthode qui consiste à réduire au maximum la fraction composée des plus grands nombres. Si, en faisant cette réduction, nous trouvons que la plus petite fraction est l’irréductible de l’autre, alors nous pouvons supposer qu’elles sont équivalentes.
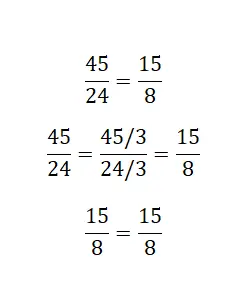
Résoudre et égaliser les divisions
Enfin, vous pouvez recourir à la solution du quotient généré par les fractions, car un nombre fractionnaire est toujours une division. Fondamentalement, vous devez calculer la valeur numérique équivalente des deux fractions, et si c’est le même nombre, alors elles seront équivalentes. Dans l’image suivante, vous pouvez voir un exemple très clair :
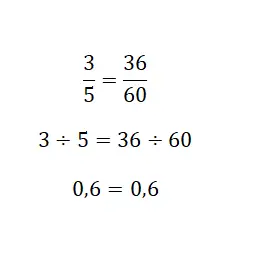
Exercices sur les fractions équivalentes
Maintenant que vous avez lu toute la théorie, vous pouvez essayer de résoudre les exercices suivants, qui vous permettront de finir de comprendre l’explication. Nous vous recommandons d’essayer de les résoudre par vous-même et une fois que vous les avez, comparez votre résultat avec celui que nous vous proposons. Cela dit, nous vous laissons pratiquer :
Exercice 1
Trouvez une fraction équivalente par simplification pour chaque fraction que nous proposons :
Pour résoudre cet exercice, il suffit d’appliquer la simplification des fractions, on obtient ainsi la fraction irréductible équivalente. Les quatre exemples sont très similaires, il n’y a donc pas beaucoup de difficulté à les résoudre.
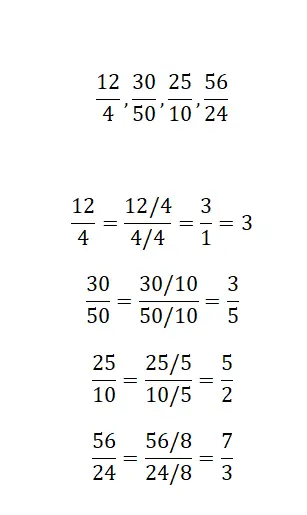
Exercice 2
Trouver une fraction équivalente par amplification pour chaque fraction que nous proposons :
Ensuite, vous devrez amplifier les fractions que nous proposons, de cette façon, vous obtiendrez des fractions équivalentes plus grandes. Peu importe le nombre que vous utilisez pour faire les multiplications, par exemple nous le ferons avec 2 et 3.
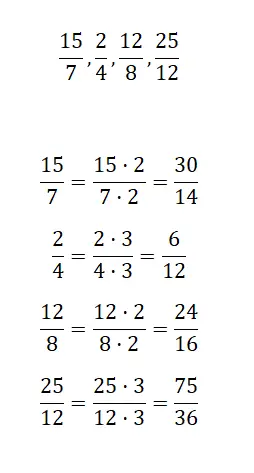
Exercice 3
Déterminez si les fractions suivantes sont équivalentes ou non :
Pour savoir si deux fractions sont équivalentes, vous devez utiliser l’une des trois méthodes que nous avons expliquées ci-dessus. Vous trouverez les corrections résolues par la première procédure, bien que vous soyez libre d’utiliser le système que vous souhaitez.
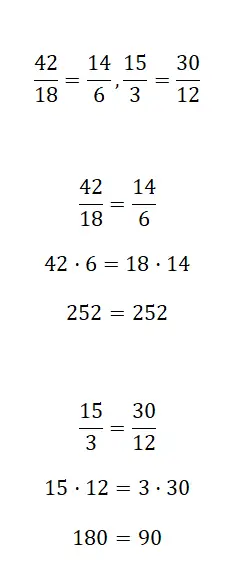
Exercice 4
Calculez les fractions équivalentes des expressions suivantes :
Dans ce dernier exercice vous devrez réécrire les expressions que nous proposons ( nombres entiers et nombres fractionnaires) sous forme de fraction, en essayant de maintenir une relation d’équivalence.