Carrés magiques

Les carrés magiques sont un jeu de réflexion mathématique qui entraîne nos compétences en calcul de manière amusante et excitante. C’est pourquoi c’est l’une des meilleures ressources pour enseigner les mathématiques aux jeunes étudiants.

Qu’est-ce qu’un tableau magique et comment est-il résolu ?

Un carré magique est une sorte de tableau ou de matrice composé de différentes cases, dans lesquelles sont écrits des nombres entiers . Mais, ils ne peuvent en aucun cas être posés, une série de règles doivent être respectées :

• Toutes les sommes magiques (sommes de toutes les valeurs de n’importe quelle ligne horizontale, verticale ou diagonale) doivent toujours donner la valeur équivalente à la constante magique (c’est une valeur unique).
• Aucun numéro ne peut être répété deux fois.
• Vous ne pouvez utiliser que des nombres consécutifs (par exemple, de 1 à 9) ou des nombres qui suivent une certaine série, par exemple : nombres impairs, multiples de 5, entre autres.

Aussi, il est important de souligner que l’on peut faire différentes classifications des carrés selon leur structure. Le premier est selon le degré du carré , qui équivaut au nombre de cellules qui sont dans une ligne ou dans une colonne. Et le second est selon le type de degré du tableau ( nombres pairs ou nombres impairs). A partir de ces distinctions, nous pouvons organiser tous les carrés en différentes catégories, bien que nous détaillerons cela plus tard.

Comment résoudre des carrés magiques ?

Pour résoudre ce jeu mathématique, nous pouvons utiliser deux méthodes différentes : utiliser la géométrie ou calculer la constante magique. Les deux procédures sont également valables, même si l’une permet d’atteindre le résultat plus rapidement, tandis que l’autre demande plus de temps et de raisonnement . Ensuite, nous expliquerons les deux méthodes, afin que vous puissiez choisir celle que vous préférez et que vous puissiez mieux vous adapter à chaque situation.

Quelle est la formule des carrés magiques ?

La première méthode consiste à calculer la constante magique , pour laquelle il faut utiliser la formule suivante : n(n ² +1)/2, où n est le degré du carré. Et une fois qu’on a cette valeur, il ne reste plus qu’à essayer les différentes combinaisons de nombres, qui permettent d’égaliser les sommes magiques du carré entier à la constante. En d’autres termes, nous devons former des combinaisons de nombres qui s’additionnent à la valeur de la constante, de manière à ce que l’ensemble du tableau soit équilibré.

Comment résoudre des carrés magiques en utilisant la géométrie ?

Deuxièmement, nous pouvons résoudre les carrés magiques au moyen de la géométrie . Bien qu’il convient de noter que cette méthode est très simple et ne vous oblige pas à exercer vos compétences en calcul, car elle est purement méthodique. Cela étant dit, nous expliquerons la procédure pour résoudre à la fois les carrés d’ordre pair et les carrés d’ordre impair.

Comment résoudre des carrés magiques avec des nombres impairs ?

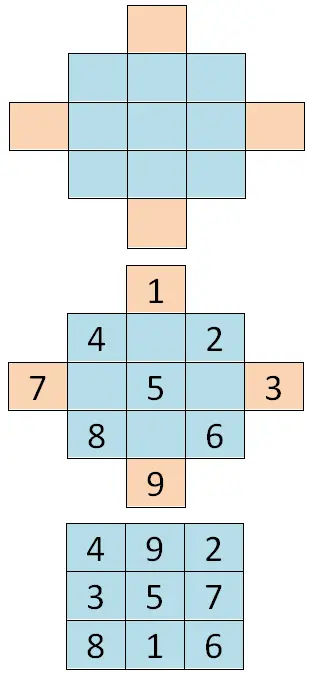
Pour résoudre ce premier cas, il faut ajouter des cellules au tableau initial de manière à avoir une sorte de losange. Ensuite, nous devons écrire tous les nombres consécutifs en commençant par le premier chiffre de la série (dans notre cas 1) et nous suivrons les diagonales du losange . Enfin, nous devons “doubler” le chiffre, par conséquent, les valeurs des cellules externes vont du côté opposé. Ainsi, les cellules extérieures de l’axe vertical se croisent, puis la même chose se produit avec les cellules de l’axe horizontal, ci-dessous vous pouvez voir un exemple :

Comment résoudre des carrés magiques d’ordre pair ?

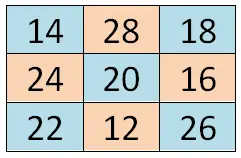
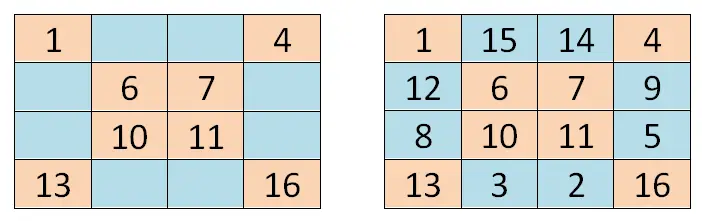
Pour résoudre un carré magique d’ordre pair (carrés magiques qui ont un nombre pair de lignes et de colonnes), nous pouvons recourir à une méthode quelque peu différente de la précédente, mais qui est également basée sur la géométrie. Nous allons commencer par écrire le premier numéro de la série (dans notre cas 1) dans le coin supérieur gauche. Ensuite, on va parcourir les deux diagonales principales et on va écrire les valeurs correspondant à la position de chaque case.

Une fois que nous aurons écrit les deux diagonales principales, nous devrons nous placer dans la première case vide en partant du coin inférieur droit (case 15 dans notre cas). Là, nous écrirons la deuxième valeur de la série et nous écrirons les valeurs restantes dans l’ordre (de la plus petite à la plus grande), en complétant les cellules de droite à gauche et de bas en haut . Pour le rendre plus clair, vous pouvez vous orienter avec l’image que nous vous montrons ci-dessous:

Comment construire des carrés magiques ?

Pour construire nous-mêmes des carrés magiques, nous pouvons suivre plusieurs procédures, parmi lesquelles nous en soulignerons deux. Il est à noter que chacun servira à créer des carrés de différents types, vous devrez donc choisir la méthode avec soin en fonction du carré que vous souhaitez générer :

méthode siamoise

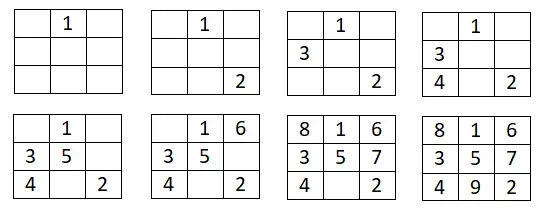
Cette première méthode est assez simple et nous aide spécifiquement à construire des carrés magiques impairs de n’importe quelle taille. La procédure à suivre est très simple, en gros on va écrire le premier numéro de la série dans la case centrale de la première rangée. A partir de là, nous remonterons dans l’ordre dans la progression arithmétique que nous avons choisie, en écrivant le nombre suivant en haut et à droite . Cependant, si cette position est en dehors du carré dessiné, nous devrons passer à la dernière ligne ou à la dernière colonne. Et si nous nous retrouvons avec une case pleine, nous devrons descendre d’une case par rapport à la case du dernier numéro que nous avons entré et ensuite nous continuerons de la même manière.

Ci-dessous vous pouvez voir un exemple de 3×3 :

Méthode de Strachey pour les carrés magiques

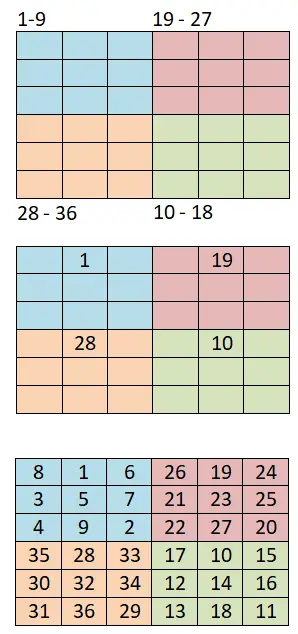
Pour générer des carrés magiques d’ordre 4k + 2 paires , nous allons utiliser cette autre méthode, qui est basée sur la précédente (la méthode siamoise) et qui est également très simple. Ci-dessous, vous pouvez voir les étapes à suivre et un exemple travaillé d’un carré magique 6×6 :

• Diviser en quadrants plus petits : la première chose que nous devons faire est de subdiviser le tableau en carrés plus petits, par exemple si nous avons un tableau 6×6, nous devrons faire quatre quadrants égaux de 3×3 carrés.
• Utilisez la méthode siamoise : ensuite nous attribuerons une plage de nombres à chaque petit quadrant, par exemple si nous commençons la séquence par 1, les plages seraient : 1-9 (premier), 10-18 (quatrième), 19-27 (deuxième) et 28-36 (troisième).

Méthode LUX de Conway pour les carrés magiques

Nous utiliserons ce dernier système lorsque nous voudrons générer des carrés magiques d’ordre 4n + 2 , où n est un nombre naturel. Ainsi, la procédure que nous allons suivre pour créer des carrés de ce style est la suivante :

• Création du tableau ou de la matrice : nous allons commencer par créer une matrice de degré 2n + 1, où n est un nombre naturel. Avec cela, nous pourrons concevoir la table et nous aurons à l’esprit son degré, puis commencerons par la conception.
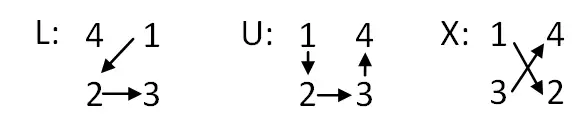
• Positionnement des lettres : une fois le tableau construit, il va falloir écrire de haut en bas : n + 1 lignes de L, 1 ligne de U et n – 1 lignes de X. Et puis, il va falloir échanger le U au milieu avec le L en haut.
• Échanger les lettres pour les valeurs numériques : maintenant, nous devrons remplacer les lettres par des groupes de quatre chiffres consécutifs. Selon la lettre, nous donnerons un ordre ou un autre aux chiffres. Expliqué ci-dessous :

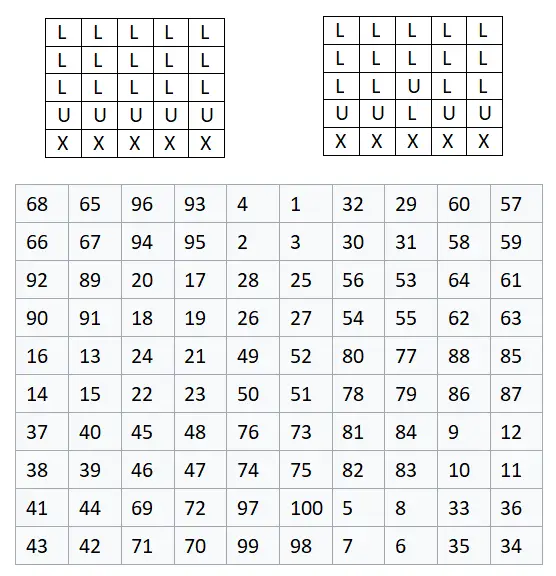
Nous allons commencer par construire une matrice 5×5 , donc n = 2, puisque : 2n + 1 = 2 · 2 + 1 = 5. Cela signifie que la matrice finira par avoir une taille de 10×10, car comme nous l’avons déjà dit, chaque cellule qui contient une lettre équivaut à un groupe de quatre nombres, soit une matrice 2×2. Ci-dessous, vous pouvez voir l’exemple fini, dans lequel nous avons remplacé chaque lettre par un groupe de quatre chiffres dans l’ordre indiqué sur l’image :

exercices de carrés magiques

Ensuite, nous vous proposons quelques carrés magiques incomplets et vous devrez les remplir vous-même, grâce aux concepts que nous avons expliqués dans cet article. Rappelez-vous que vous pouvez utiliser n’importe laquelle des méthodes enseignées. De plus, vous devez tenir compte du fait que 1 n’est peut-être pas le premier numéro de la série, même s’il le mettra dans la déclaration. Et lorsque vous aurez terminé l’un des exercices, vous pourrez voir la solution sous l’énoncé.

Carré magique 3×3

Construisez un carré magique 3×3 avec uniquement des nombres impairs :

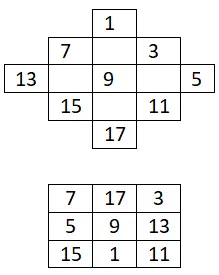
Carré magique 4×4

Complétez le carré magique 4×4 suivant :

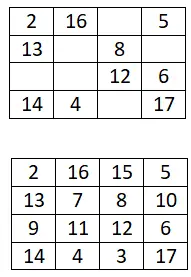
Carré magique 5×5

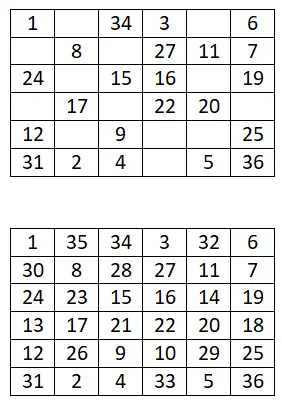
Complétez le carré magique 5×5 suivant :

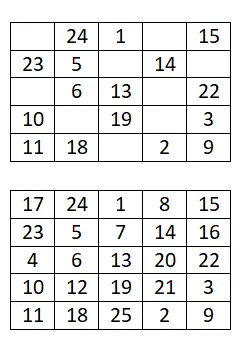
Carré magique 6×6

Complétez le carré magique 6×6 suivant :