Les rapports trigonométriques d’un angle sont les rapports obtenus à partir des trois côtés d’un triangle rectangle. En d’autres termes, ce sont les valeurs qui résultent de la comparaison de ses trois côtés au moyen de quotients (divisions). Bien qu’il convient de noter que ces raisons n’existent que dans les triangles rectangles (triangles qui ont un angle de 90º).
Rapports trigonométriques dans un triangle rectangle
Les six rapports trigonométriques les plus importants sont : sinus, cosinus, tangente, cosécante, sécante et cotangente. Ensuite, nous expliquerons en détail comment chacune de ces raisons est définie et nous parlerons de la formule qui les caractérise. Afin de comprendre les explications suivantes nous prendrons en compte le triangle rectangle suivant :

Sein
Le sinus d’un angle (sin ou sin) est égal au quotient de la jambe opposée (a) entre l’hypoténuse (c), par conséquent, la formule du sinus est la suivante : sin (α) = a / c . Il est très important de connaître cette définition du sinus, car c’est la base de toute trigonométrie, ainsi que les autres raisons que nous aborderons dans cette section.
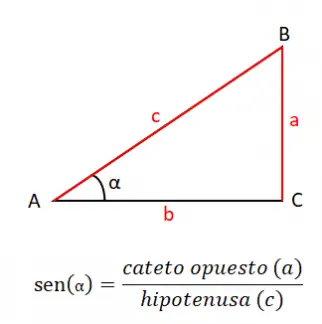
Trav C’est à partir du théorème des sinus, nous pouvons calculer n’importe quel côté du triangle , nous pouvons le faire en reliant les quotients d’un certain angle entre son côté correspondant. Par exemple, si nous voulons calculer le côté a et que nous avons les valeurs du côté par des angles A et B, nous pouvons le faire en utilisant la formule : a / sin (A) = b / sin (B) . En résolvant cette équation simple, nous obtenons la valeur correspondant à la variable que nous voulons calculer.
Cosinus
Le cosinus d’un angle (cos) est égal au quotient de la jambe adjacente (b) entre l’hypoténuse (c), par conséquent, la formule du cosinus est la suivante : cos (α) = b / c . Dans ce cas, la formule est composée des deux côtés du triangle qui sont en contact avec l’angle que l’on veut étudier, dans cet exemple, l’angle A ou α.
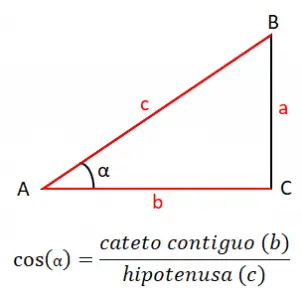
Avec le cosinus, nous avons également un moyen de calculer les côtés du triangle , qui provient du théorème du cosinus. Cela nous permet de relier les côtés aux angles et nous offre les trois expressions suivantes :
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Tangente
La troisième raison la plus importante, avec laquelle nous fermerons l’ensemble des raisons originales, est la tangente (tan ou tg). Ceci est calculé en divisant entre la jambe opposée (a) et la jambe adjacente (b), par conséquent, la formule de tangente est la suivante : tan (α) = a / b . Vous pouvez le voir graphiquement ci-dessous :
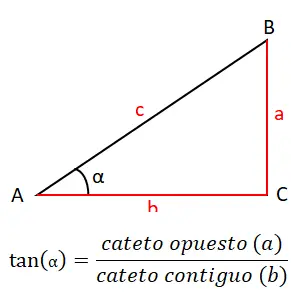
La tangente a également son propre théorème, appelé théorème de tangente. Cela nous permet de relier les longueurs de deux côtés d’un triangle avec les tangentes des angles . L’énoncé est le suivant : “le quotient de la somme de deux côtés entre leur soustraction est égal au quotient entre la tangente de la moyenne des deux angles opposés à ces côtés et la tangente de la moitié de la différence de ceux-ci”.
Rapports trigonométriques dérivés
A partir des trois rapports trigonométriques dont nous venons de parler, on peut obtenir d’autres rapports trigonométriques dérivés. Ceux-ci sont obtenus en faisant le rapport inverse par rapport au sinus, au cosinus et à la tangente.
- Cosécante : est le rapport inverse du sinus et se calcule avec les formules : cosec (α) = c / a et cosec (α) = 1 / sin (α).
- Sécante : est le rapport inverse du cosinus et se calcule avec les formules : sec (α) = c / b et sec (α) = 1 / cos (α).
- Cotangente : est le rapport inverse de la tangente et se calcule avec les formules : cotg (α) = b / a et cotg (α) = 1 / tan (α).
Tableau des rapports trigonométriques
Ci-dessous, vous pouvez voir un tableau qui résume toutes les raisons expliquées jusqu’à présent. Avec ce tableau, vous pourrez mémoriser efficacement toutes les formules, car il vous permet de distinguer facilement les différences entre chaque expression mathématique.
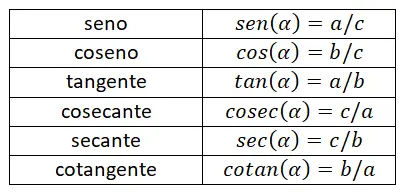
Rapports trigonométriques dans un cercle
Une autre façon d’étudier la trigonométrie est à travers la circonférence goniométrique ou cercle unité , cette circonférence a un rayon égal à 1 et son origine est le point (0, 0). Le dessin se compose d’un cercle et d’un triangle rectangle représenté à l’intérieur du cercle, plus précisément, l’angle que nous allons étudier doit toucher le point d’origine.
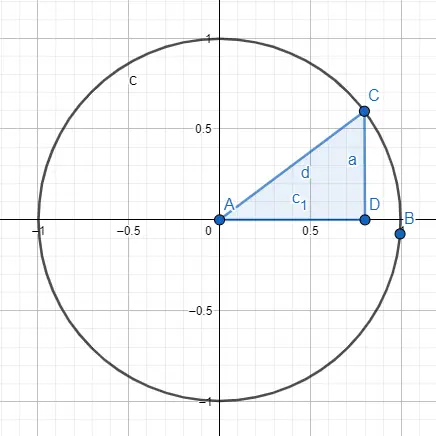
Lorsque nous avons cette image, nous savons que le rayon est égal à l’hypoténuse, qui est égal à 1. Donc, si nous voulons calculer le sinus et le cosinus, nous utiliserons la valeur du rayon et la valeur des autres côtés du triangle. Pour calculer le sinus, on va faire le calcul suivant : sin (A) = CD / AC = CD / rayon = CD / 1 = CD , donc le sinus de A est a. Par contre, pour calculer le cosinus, on va faire le calcul : cos (A) = AD / AC = AD / rayon = AD / 1 = AD , du coup le cosinus de A est c1.
Il est très important de garder deux choses à l’esprit. La première est que l’utilisation de ce cercle dans l’étude des rapports trigonométriques est due à la nécessité de traiter des angles plus grands que ceux qui peuvent être étudiés avec le triangle. Par exemple, l’angle de 150º ne peut pas être étudié à travers un simple triangle, car il est trop grand. Et la deuxième chose à garder à l’esprit est que le sinus et le cosinus ne peuvent jamais adopter des valeurs supérieures à 1 et inférieures à -1.
Signe des rapports trigonométriques
Comme nous l’avons dit précédemment, pour traiter des angles plus grands que ceux qu’un triangle nous permet de traiter, nous utilisons la circonférence goniométrique. Pour ce faire, nous représentons un triangle à l’intérieur du cercle exactement dans l’un des quatre quadrants qui divisent la circonférence, dans l’image suivante, vous pouvez voir les quatre quadrants représentés.
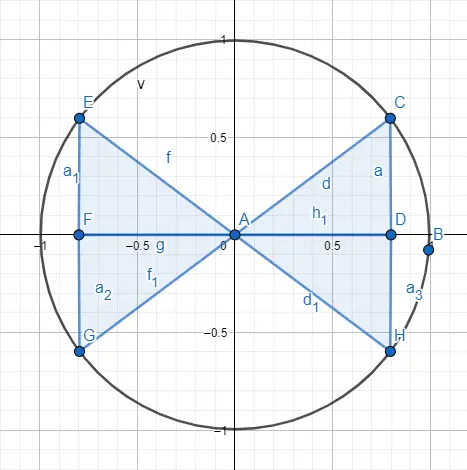
Donc, pour faire la distinction entre un angle de 30 et un de 210, qui deviennent le même concernant la distribution à l’intérieur du triangle , nous utiliserons une répartition des signes selon le quadrant dans lequel se trouve le triangle. Ci-dessous, vous pouvez voir les signes correspondant à chaque quadrant et un exemple dessiné.
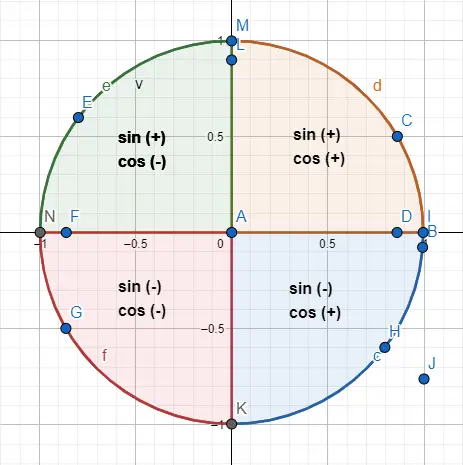
Par exemple, les angles 30º et 210º partagent la même valeur numérique , mais leur sinus et cosinus ont des signes opposés. Donc : sin(30) = 1/2 et cos(30) = √3/2, alors que sin(210) = -1/2 et cos(210) = -√3/2. Pour arriver à ce résultat nous avons représenté les deux angles sur la circonférence (image ci-dessous) et nous avons suivi les indications des signes.
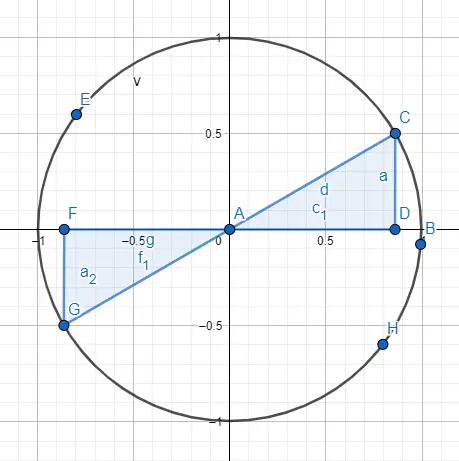
Enfin, commentez qu’il est possible d’avoir des angles supérieurs à 360º , bien que cela puisse ne pas sembler être le cas car la circonférence n’est que de 360º. Mais, si nous voulons résoudre pour un angle de 750º, nous pouvons faire une réduction à un angle compris entre 0º et 360º. Simplement, nous divisons 750 par 360 et le reste est l’angle qui reste, dans le cas de 750º nous obtenons un angle de 30º.
Types d’angles selon le quadrant
Il existe des relations entre différents angles, qui nous permettent de calculer les rapports valeurs trigonométriques de tous les angles appartenant au cercle. Laissez-nous obtenir ces raisons de la réduction au premier quadrant . Cela signifie que nous faisons une simplification d’un certain angle au premier quadrant et appliquons ensuite les signes correspondants. Vous trouverez ci-dessous les différentes procédures expliquées (selon le quadrant):
premier quadrant
Dans ce premier quadrant (0º – 90º), nous n’avons qu’à résoudre le rapport trigonométrique avec l’angle qui nous a été donné. Et si nous regardons l’image que nous avons expliquée précédemment à propos des symboles, le sinus et le cosinus ont un positif devant eux (le résultat que nous obtenons ne sera pas affecté par le signe).
Réduction du deuxième quadrant au premier
Dans le deuxième quadrant (90º – 180º) nous avons affaire à des angles supplémentaires, ce qui signifie que les deux angles totalisent 180º. Par conséquent, nous devons faire une réduction du deuxième quadrant au premier et nous le faisons avec la formule 180 – α = β , où α est l’angle du premier quadrant et β est l’angle d’origine.
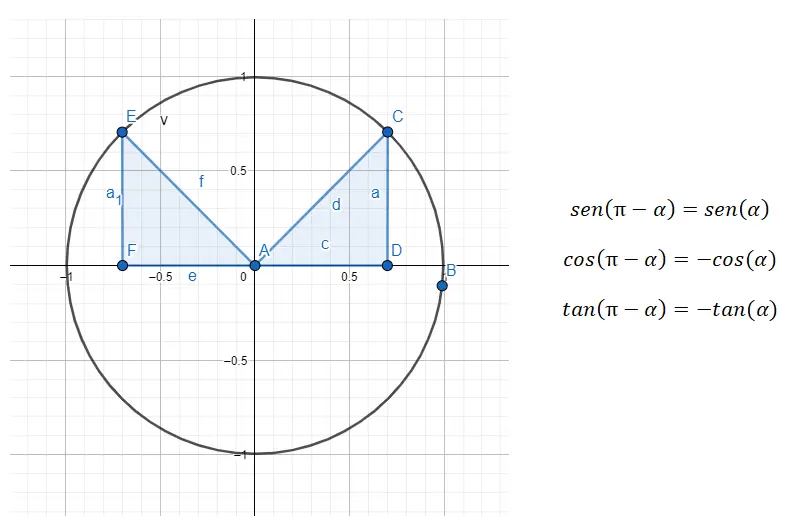
Par exemple, si on nous donne l’angle 135º (qui appartient au deuxième quadrant), nous devons trouver l’angle du premier quadrant qui est lié à ce premier. Dans cet exemple, l’angle (α) que nous recherchons est de 45º, puisque 180 – 45 = 135. Donc, ce sera vrai : sin (135) = sin (180 – 45) = sin (45), cos (135) = cos (180 – 45) = -cos (45) et tan (135) = tan (180 – 45) = -tan (45).
Réduction du troisième quadrant au premier
Dans le troisième quadrant (180º – 270º) , nous avons affaire à des angles qui diffèrent de 80º, ce qui signifie que les angles sont distants de 180º. Donc, si nous voulons réduire du troisième quadrant au premier, nous devons utiliser la formule 180 + α = β , où α est l’angle du premier quadrant et β est l’angle d’origine.
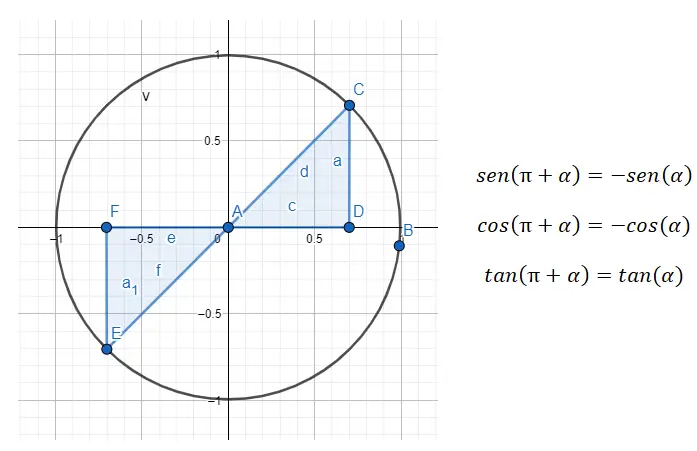
Par exemple, si on nous donne l’angle 225º (qui appartient au troisième quadrant), nous devons trouver l’angle du premier quadrant qui lui correspond. Dans le cas de 225º, l’angle (α) que nous recherchons est à nouveau de 45º, puisque 180 + 45 = 225. Donc, sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) et tan (225) = tan (180 + 45) = tan (45 ) sera satisfait. ).
Réduction du quatrième quadrant au premier
Dans le quatrième quadrant (270º – 360º) nous avons affaire à des angles opposés, ce qui signifie que les angles sont numériquement égaux, mais de signes opposés , comme 30º et -30º (équivalent à 330º, puisque 360º – 30º = 330º) . Il est important de garder à l’esprit que les angles opposés peuvent être écrits comme un angle positif et un angle négatif ou comme deux angles positifs (dans l’exemple que nous venons de discuter, nous avons expliqué la différence).
Donc, si nous voulons faire une réduction du quatrième quadrant au premier, nous devons utiliser la formule 360 – α = β , où α est l’angle du premier quadrant et β est l’angle d’origine.
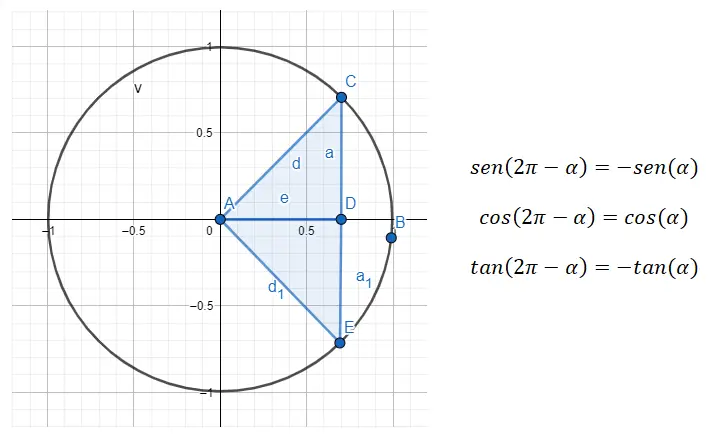
Par exemple, si on nous donne l’angle 315º (qui appartient au quatrième quadrant), nous devons trouver l’angle du premier quadrant qui est lié à ce premier. Dans le cas de l’angle (α) que nous recherchons, c’est encore 45º, puisque, 360 – 45 = 315. Donc, sin (315) = sin (360 – 45) = -sin (45), cos (315) = cos (360 – 45) = cos (45) et tan (315) = tan (360 – 45) = -tan (45). En conclusion, nous avons vu les angles dérivés de 45º de tous les quadrants.
Rapports trigonométriques des angles les plus importants
Il existe un certain nombre d’angles, appelés angles notables , qui sont les plus courants en trigonométrie. Connaître vos rapports trigonométriques par cœur est fortement recommandé. Par conséquent, ci-dessous, nous avons créé un tableau contenant les rapports trigonométriques de ces angles et leurs dérivées (mêmes angles, mais avec une différence de 90, 180 ou 270 degrés) :
| Angle (°) | Angle (rad) | Sein | Cosinus | Tangente |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 πrad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60º | 1/3 πrad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 πrad | -√2/2 | √2/2 | -1 |
Relation entre les rapports trigonométriques
Il existe plusieurs façons de relier les différents rapports trigonométriques. A partir de ces relations, on obtient une sorte d’égalités entre les différentes fonctions trigonométriques, qu’on appelle des identités trigonométriques. Grâce à ce type d’identités, nous pouvons calculer un rapport basé sur n’importe quel autre. Il convient de noter qu’il existe de nombreux types différents d’identités trigonométriques, qui sont classées en fonction du type de relation qui prend en charge l’expression elle-même.
Problèmes résolus de rapports trigonométriques
Ensuite, nous vous proposons une série d’exercices avec lesquels vous pourrez mettre en pratique toute la théorie expliquée dans cet article. N’oubliez pas que si à tout moment vous êtes bloqué ou avez des questions, vous pouvez relire l’article et sûrement, avec une seconde lecture , vous comprendrez tout beaucoup mieux. Cela dit, vous pouvez commencer à pratiquer :
Exercice 1
Calculez les six rapports trigonométriques de l’angle de 225º :
Nous allons commencer par calculer l’angle (α), qui est égal à : 180 + α = 225º, donc α = 45º.
sin(225) = sin(180 + 45) = -sin(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
bronzer(225) = bronzer(180 + 45) = bronzer(45) = 1
Exercice 2
Calculez les six rapports trigonométriques de l’angle de 120º :
Nous allons commencer par calculer l’angle (α), qui est égal à : 180 – α = 120º, donc α = 60º.
péché(120) = péché(180 – 60) = péché(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
Exercice 3
Calculez les six rapports trigonométriques de l’angle de 510º :
Avant de commencer, il faut faire la réduction d’angle : 510 / 360 = 1 tour et un angle de 150 restant. Ensuite, nous calculons l’angle (α), qui est égal à : 180 – α = 150, donc α = 30º.
péché(150) = péché(180 – 30) = péché(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3