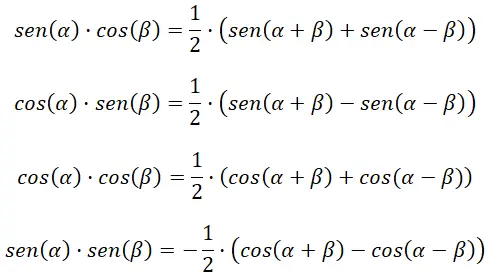Les identités trigonométriques sont des égalités entre les différentes fonctions trigonométriques. Grâce à ces équivalences trigonométriques, on peut déduire un certain rapport trigonométrique basé sur n’importe quel autre. Par conséquent, il est nécessaire de connaître les formules de ces rapports afin de comprendre les formules des identités trigonométriques. Si vous ne les connaissez pas dans votre cas, nous vous recommandons de visiter le dernier lien.
Tableau des identités trigonométriques
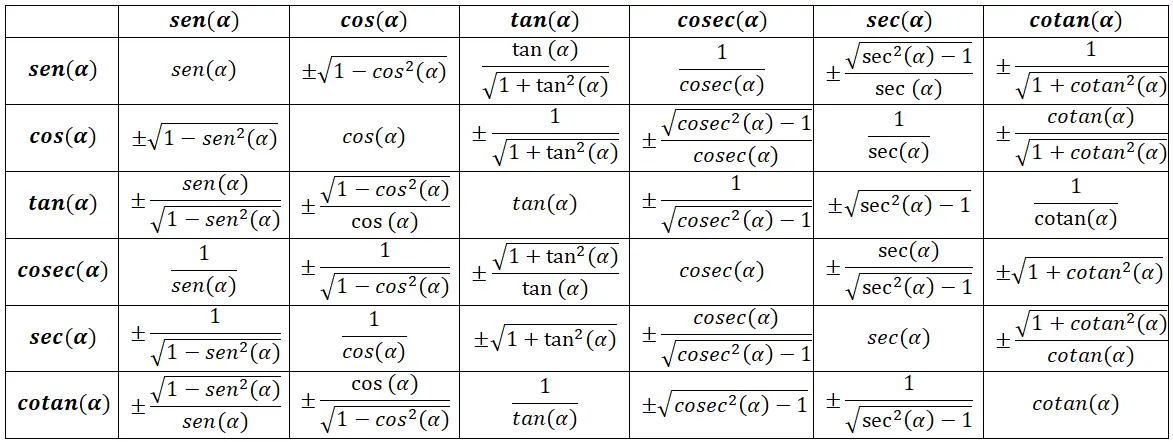
Identités trigonométriques fondamentales
Il existe une série d’identités trigonométriques de base qui sont considérées comme les plus importantes, car elles constituent la base théorique des autres. Ce sont les plus courants à trouver et probablement les plus faciles à retenir, car ils sont assez intuitifs. N’oubliez pas que toutes les formules seront basées sur l’image suivante :

Identité trigonométrique fondamentale
La première identité de toutes est ce que l’on appelle l’identité trigonométrique fondamentale , également connue sous le nom de relation entre le sinus et le cosinus. Vous trouverez ci-dessous sa preuve mathématique : sin² (α) + cos² (α) = 1.
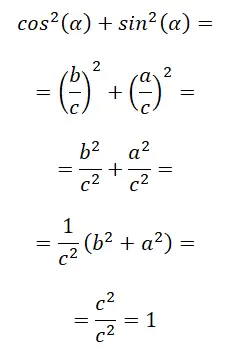
Dans la dernière étape, nous appliquons essentiellement le théorème de Pythagore, car c² = a² + b², il nous reste alors c² / c² qui est égal à 1. En conclusion, nous pouvons affirmer que : sin² (α) + cos² (α) = 1.
Relation entre sécante et tangente (sécante au carré)
Deuxièmement, nous avons une identité trigonométrique qui relie la sécante à la tangente, son expression est la suivante : sec² (α) = 1 + tan² (α) . Dans l’image suivante vous pouvez voir quelques formules de rappel qui composent cette identité puis la marche à suivre pour arriver à la formule finale :
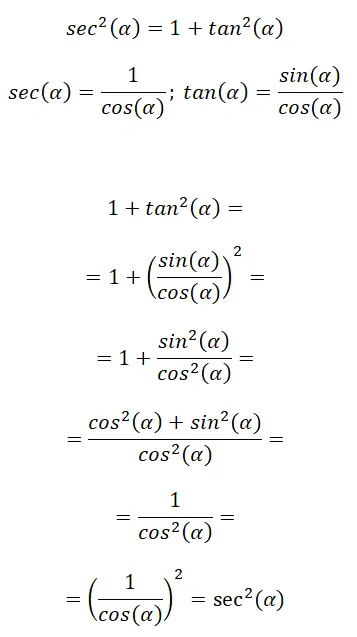
Dans ce cas, nous utilisons les formules de rapport trig pour trouver d’autres rapports. En conclusion, on peut dire que : sec² (α) = 1 + tan² (α).
Relation entre cosécante et cotangente (cosécante au carré)
De la définition de cosécante et cotangente on peut trouver un lien dans la formule de la tangente, c’est grâce à cela qu’on peut déduire une autre identité trigonométrique : cosec² (α) = 1 + cotg² (α) .
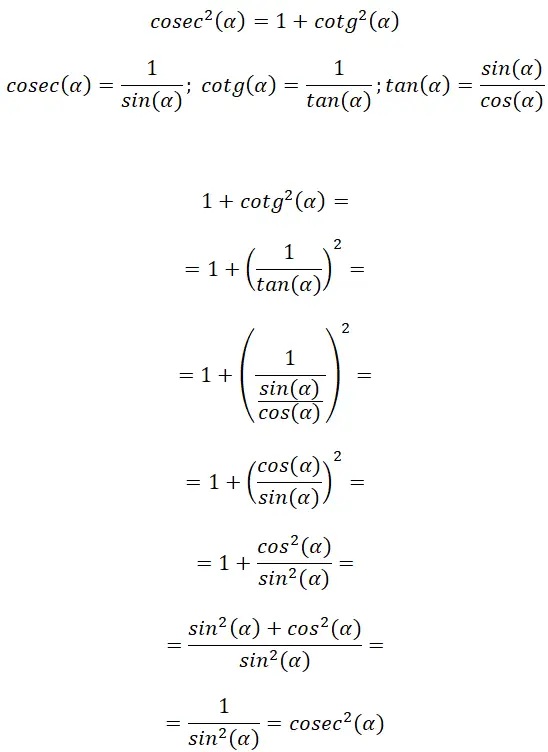
Avec cette démonstration on peut vérifier que : cosec² (α) = 1 + cotg² (α). De plus, nous pouvons voir que cette relation présente une certaine similitude avec la précédente, qui est due à la similitude entre tangente et cotangente.
Rapports trigonométriques de l’angle de somme et de l’angle de soustraction
Les rapports de somme d’angle ou de soustraction d’angle sont un type d’identités obtenues en calculant les rapports trigonométriques de l’addition ou de la soustraction de deux angles. Par exemple, si nous voulons calculer le sinus de 90 + 60, il existe une série de formules qui facilitent ce calcul. Vous trouverez ci-dessous une liste avec toutes les formules des identités trigonométriques de ce style :
Sinus de la somme des angles : sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Sinus de la soustraction d’angle : sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Cosinus de la somme des angles : cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Soustraction du cosinus angulaire : cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Tangente de la somme des angles : tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Soustraction tangente angulaire : tan (α – β ) = (tan (α) + tan ( β )) ÷ (1 + tan (α) tan ( β ))
Il est évident que calculer le sinus de 150º est plus facile que d’utiliser les formules que nous venons d’expliquer pour calculer le sinus de (90º + 60º). Alors pourquoi ces formules sont-elles importantes ? Eh bien, la réponse est que ces identités nous permettent de calculer les rapports trigonométriques d’ angles complexes à partir d’angles plus simples. Par conséquent, si nous mémorisons les rapports des angles notables (les plus pertinents), nous n’aurons pas besoin d’utiliser la calculatrice pour calculer les rapports des angles plus complexes tels que 150º.
Rapports trigonométriques à double angle
Lorsque nous voulons calculer les rapports trigonométriques d’un angle double (2α) , nous pouvons le faire au moyen d’une série d’identités. Plus précisément, nous pouvons le faire grâce à des formules très similaires à celles dont nous venons de discuter dans la section précédente. Puisque, si nous changeons β en α, dans les expressions précédentes, il nous reste (α + α), ce qui équivaut à (2α). En gardant cela à l’esprit, nous pouvons déduire les identités suivantes :
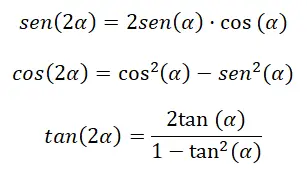
Vous pouvez voir les démos ci-dessous :
Sinus du double angle : sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Cosinus du double angle : cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Tangente à angle double : tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Rapports trigonométriques du demi-angle
Aussi, il existe des identités qui permettent de calculer les rapports trigonométriques du demi-angle (α/2) :
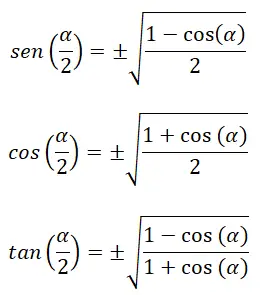
Parmi les formules déjà connues suivantes :
1 = sin² ( β ) + cos² ( β )
cos (2 β ) = cos² ( β ) – sin² ( β )
Si nous faisons β = α/2, alors nous pouvons prouver ces identités, en soustrayant les deux expressions dans le cas du sinus, en les ajoutant dans le cas du cosinus, et en divisant les deux formules obtenues (celle du sinus et celle du cosinus) dans le cas de la tangente. Seulement, il reste à isoler le ratio que l’on veut calculer dans les formules que l’on obtient ci-dessous :
Demi angle sinus : 1 – cos (α) = 2 sin² (α/2) ; sin² (α/2) = (1 – cos (α)) ÷ 2
Cosinus demi-angle : 1 + cos (α) = 2 cos² (α/2) ; cos² (α/2) = (1 + cos (α)) ÷ 2
Rapports trigonométriques de l’angle triple
Dans le cas d’avoir un angle triple (3α) , on peut aussi utiliser certaines identités pour calculer leurs rapports trigonométriques. Ces identités proviennent des formules suivantes déjà expliquées : les identités d’angle double, les identités d’angle somme et l’identité fondamentale de la trigonométrie.
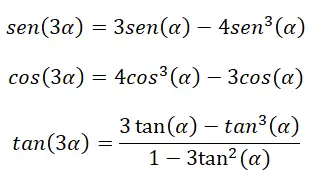
Pour prouver ces identités, nous devons recourir aux formules de somme des angles :
Sinus de la somme des angles : sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Cosinus de la somme des angles : cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Donc, si nous appliquons les formules à double angle dans les expressions dont nous venons de parler et appliquons l’identité fondamentale de la trigonométrie, nous pouvons prouver les identités. Il convient de mentionner que l’utilisation de l’identité trigonométrique fondamentale nous permet de convertir tous les rapports de l’expression en un seul. C’est pourquoi la formule du sinus de l’angle triple n’est composée que de sinus et celle du cosinus ne contient que des cosinus. Ci-dessous, vous pouvez voir la procédure complète :
Sinus de l’angle triple : sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin³ (α) – sin³ (α) + 2 sin (α) – 2 sin³ (α) =
= 3 sin (α) – 4 sin³ (α)
Cosinus de l’angle triple : cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Enfin, la tangente de l’angle triple peut être calculée de deux manières : la première en divisant la formule du sinus par la formule du cosinus et la seconde en substituant l’expression de la tangente de l’angle double, dans la formule suivante à la tangente de l’angle somme : tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α)).
Identités trigonométriques selon le type d’angle
Il est important de commenter une série de formules qui sont en quelque sorte des règles permettant de calculer directement et rapidement des rapports trigonométriques. En fait, elles peuvent aussi être considérées comme des identités trigonométriques, puisqu’elles répondent aux mêmes caractéristiques que toutes les expressions dont nous venons de parler. Plus précisément, ces formules nous permettent de déterminer les rapports trigonométriques d’un angle à partir de la relation qu’il entretient avec un autre angle.
angles complémentaires
Les angles complémentaires (α et β ) sont ceux qui ont une somme égale à 90º, donc, lorsque nous les additionnons, nous obtenons un angle droit. Pour déterminer que α est l’angle complémentaire de β , il faut résoudre une équation très simple : α = 90 – β , si le résultat de cette équivalence concorde, alors on peut affirmer qu’ils sont complémentaires. Grâce à ces identités on peut déduire les rapports trigonométriques d’un angle de ceux de l’autre.
Sinus de l’angle complémentaire : sin (90º – α) = cos (α)
Cosinus de l’angle complémentaire : cos (90º – α) = sin (α)
Tangente de l’angle complémentaire : tan (90º – α) = cotan (α)
Cosécante de l’angle complémentaire : cosec (90º – α) = sec (α)
Sécante de l’angle complémentaire : sec (90º – α) = cosec (α)
Cotangente de l’angle complémentaire : cotan (90º – α) = tan (α)
angles supplémentaires
Les angles supplémentaires (α et β ) sont ceux qui ont une somme égale à 180º ou π radians, on peut donc en déduire la formule α + β = 180º. Ou, en d’autres termes, si l’angle supplémentaire de α est β , alors l’expression suivante β = 180 – α doit être satisfaite. Ensuite, vous pouvez voir la liste des identités que nous pouvons déduire de ces angles :
Sinus de l’angle supplémentaire : sin (180º – α) = sin (α)
Cosinus de l’angle supplémentaire : cos (180º – α) = -cos (α)
Tangente de l’angle supplémentaire : tan (180º – α) = -tan (α)
Cosécante de l’angle supplémentaire : cosec (180º – α) = cosec (α)
Sécante de l’angle supplémentaire : sec (180º – α) = -sec (α)
Cotangente de l’angle supplémentaire : cotan (180º – α) = -cotan (α)
angles conjugués
Les angles conjugués (α et β ) sont ceux qui ont une somme égale à 360º ou 2π radians, c’est pourquoi on peut en déduire la formule α + β = 360º. Et à partir de cette première formule, on peut exprimer l’un des angles en fonction de l’autre comme suit : α = 360º – β ou β = 360º – α. Nous allons maintenant vous montrer les égalités des angles conjugués :
Sinus de l’angle conjugué : sin (360º – α) = – sin (α)
Cosinus de l’angle conjugué : cos (360º – α) = cos (α)
Tangente de l’angle conjugué : tan (360º – α) = – tan (α)
Cosécante de l’angle conjugué : cosec (360º – α) = – cosec (α)
Sécante de l’angle conjugué : sec (360º – α) = sec (α)
Cotangente de l’angle conjugué : cotan (360º – α) = – cotan (α)
angles opposés
Les angles opposés ou angles négatifs (α et β ) sont ceux qui ont la même valeur numérique, mais ont des signes différents, un exemple de ce type d’angle est 30º et -30º. Il ne faut pas oublier que le signe négatif indique que la rotation se fait dans le sens des aiguilles d’une montre, tandis qu’un angle positif tourne dans le sens inverse des aiguilles d’une montre.
Sinus de l’angle opposé : sin (-α) = – sin (α)
Cosinus de l’angle opposé : cos (-α) = cos (α)
Tangente de l’angle opposé : tan (-α) = – tan (α)
Cosécante de l’angle opposé : cosec (-α) = – cosec (α)
Sécante de l’angle opposé : sec (-α) = sec (α)
Cotangente de l’angle opposé : cotan (-α) = – cotan (α)
Angles qui diffèrent de 90º ou angles plus/moins π/2
Les angles qui diffèrent de 90º ou les angles plus/moins π/2 (α et β ) sont ceux qui ont une différence de 90º. Par conséquent, ils peuvent être exprimés sous la forme β – α = 90º, où β est supérieur de 90º à α . Ces angles ont également une série de formules qui relient les rapports trigonométriques des deux angles.
Sinus de l’angle qui diffère de 90º : sin (90º + α) = cos (α)
Cosinus de l’angle qui diffère de 90º : cos (90º + α) = -sin (α)
Tangente de l’angle qui diffère de 90º : tan (90º + α) = – cotan (α)
Cosécante de l’angle qui diffère de 90º : cosec (90º + α) = sec (α)
Sécante de l’angle qui diffère de 90º : sec (90º + α) = -cosec (α)
Cotangente de l’angle qui diffère de 90º : cotan (90º + α) = -cotan (α)
Angles qui diffèrent de 180º ou angles plus/moins π
Les angles plus/moins π (α et β ) sont équivalents à des angles qui diffèrent de 180º. Par conséquent, ils peuvent être exprimés au moyen de la formule suivante : β – α = 180º, où β 180º est supérieur à α . Ensuite, nous vous montrons les identités trigonométriques qui relient les rapports trigonométriques de ces angles :
Sinus de l’angle qui diffère de 180º : sin (180º + α ) = -sin ( α )
Cosinus de l’angle qui diffère de 180º : cos (180º + α ) = -cos ( α )
Tangente de l’angle qui diffère de 180º : tan (180º + α ) = tan ( α )
Cosécante de l’angle qui diffère de 180º : cosec (180º + α ) = -cosec ( α )
Sécante de l’angle qui diffère de 180º : sec (180º + α ) = -sec ( α )
Cotangente de l’angle qui diffère de 180º : cotan (180º + α ) = cotan ( α )
Transformations de rapports trigonométriques
Enfin, il existe des identités trigonométriques qui nous permettent d’exprimer un certain rapport trigonométrique au moyen d’ autres opérations . Donc, si nous avons une somme de rapports et que nous voulons l’exprimer sous forme de produit, nous pouvons recourir à ces formules. Bien que, malheureusement, il n’y ait pas d’expression pour chaque opération arithmétique, vous ne pouvez passer que de l’addition ou de la soustraction au produit et vice versa .
Convertir l’addition ou la soustraction en produit
Les quatre formules suivantes nous aident à calculer l’addition et la soustraction des fonctions trigonométriques :
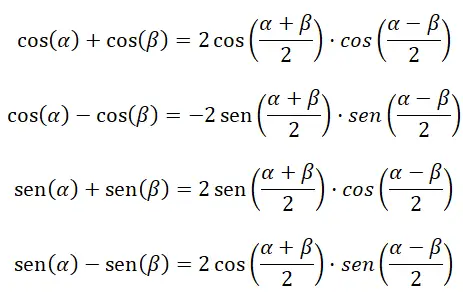
Transformer le produit en addition ou soustraction
Les quatre formules suivantes nous aident à calculer les produits des fonctions trigonométriques :