Quel est le nombre Pi ?

Le nombre Pi est uneconstante mathématique qui représente la relation entre la circonférence d’un cercle et son diamètre. C’est un nombre irrationnel. Autrement dit, ce n’est pas une fraction exacte . Par conséquent, il ne peut pas être représenté comme un nombre décimal fini. La valeur de Pi est d’environ 3,14159 et est représentée par la lettre grecque π.

Pi est un nombre important en mathématiques. Par conséquent, il a de nombreuses applications dans divers domaines. Par exemple, il est utilisé en géométrie pour calculer l’aire. En outre, le périmètre des cercles et autres figures circulaires. D’autre part, en trigonométrie pour calculer des angles et des longueurs d’arcs. Enfin, en ingénierie et en physique pour calculer des quantités telles que le volume et la capacité.

Le Pi Day est célébré le 14 mars de chaque année, car la date se rapproche de la valeur de Pi (3,14). Cette date est célébrée pour commémorer le rôle de Pi dans les mathématiques et promouvoir l’intérêt pour cette constante fondamentale.

Qui a découvert le nombre Pi ?

Le nombre Pi est connu depuis l’Antiquité, et c’est le mathématicien grec Archimède (287-212 av. J.-C.) qui le décrit avec précision. En fait, il l’utilisait pour calculer l’aire et le volume de figures géométriques.

Au 18ème siècle, le mathématicien suisse Johann Lambert a prouvé que Pi est un nombre irrationnel . Plus tard, au XIXe siècle, le mathématicien allemand Ferdinand von Lindemann a expliqué que Pi est un nombre transcendantal . Autrement dit, il ne peut pas être exprimé comme une solution exacte d’une équation polynomiale avec des coefficients rationnels.

Tout au long de l’histoire, différents mathématiciens ont contribué à la compréhension du nombre Pi et ont développé des techniques pour le calculer avec une plus grande précision. Aujourd’hui, Pi reste l’une des constantes mathématiques les plus importantes et les plus connues au monde et continue d’être un sujet d’étude en mathématiques.

Pourquoi le nombre Pi est-il infini ?

La valeur de Pi est d’environ 3,14159, mais en réalité, c’est un nombre qui continue indéfiniment après la virgule. Cela signifie que Pi est un nombre infini et ne peut pas être entièrement représenté par un nombre décimal.

Bien que la valeur de Pi soit infinie, en pratique des valeurs approximatives de Pi peuvent être calculées avec une grande précision. À l’heure actuelle, des millions de chiffres de Pi ont été calculés et il a été démontré qu’il n’a pas de motifs réguliers dans ses chiffres décimaux. Bien que cela ait été fait via des superordinateurs, car nous ne pouvons pas calculer autant de chiffres.

Quelles méthodes existent pour calculer la valeur approchée du nombre Pi ?

Il existe plusieurs méthodes pratiques pour calculer la valeur de Pi. Ensuite, nous expliquons étape par étape les trois méthodes les plus utilisées par les mathématiciens.

1. Méthode d’Archimède

Le mathématicien grec Archimède a utilisé une méthode géométrique pour calculer une valeur approximative de Pi. Pour utiliser cette méthode, suivez les étapes ci-dessous :

1. Dessinez un cercle et tracez une ligne passant par le centre du cercle et coupez-la en deux points opposés, comme indiqué ci-dessous :

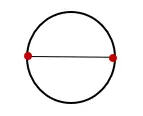
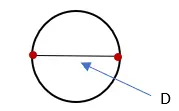
2. Mesurez la longueur de la ligne qui coupe le cercle et appelez-la “D”. Cette mesure est le diamètre du cercle.

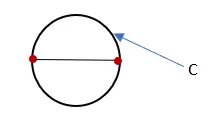
3. Mesurez la longueur de la ligne qui forme le cercle et étiquetez-la « C ». Cette mesure est la circonférence du cercle.

4. Divisez la circonférence du cercle (C) par le diamètre du cercle (D). Le résultat est une valeur approximative de Pi.

Par exemple : si le diamètre du cercle est de 6 et la circonférence de 18, alors la valeur approximative de Pi est de 18 ÷ 6 = 3. Évidemment, cet exemple est très basique, mais si vous le faites avec des valeurs d’une circonférence réelle , vous verrez que la méthode fonctionne correctement.

En fait, nous vous recommandons d’essayer de le faire : prenez les mesures d’une tasse ou de quelque chose qui a une forme circulaire et voyez si cela fonctionne pour vous.

2. Méthode de Monte Carlo

La méthode de Monte Carlo est une méthode probabiliste utilisée pour calculer des valeurs approximatives de Pi. Pour ce faire, un grand nombre de points sont générés aléatoirement sur un plan et le nombre de points qui rentrent dans un cercle inscrit dans un carré est compté. Le processus est appliqué comme suit :

1. Dessinez un cercle à l’intérieur d’un carré de côté 1, comme indiqué ci-dessous :

2. Générez aléatoirement un grand nombre de points dans le carré.

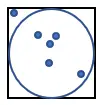
3. Comptez le nombre de points qui rentrent dans le cercle. Appelons cette quantité “n”.

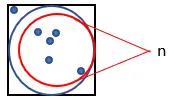
4. Comptez le nombre total de points générés. Appelez cette quantité “m”.

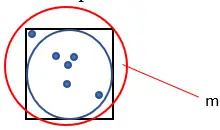
5. Calculez la valeur approximative de Pi à l’aide de la formule suivante : Pi = (4 · n) ÷ m.

Par exemple, si 380 points ont été générés et que 300 rentrent dans le cercle, alors la valeur approximative de Pi est (4 · 300) ÷ 380 = 3,16. Cette valeur ressemble beaucoup aux deux premières décimales de Pi, mais tout comme la méthode précédente, l’utilisation de mesures réelles vous donnera une valeur encore plus précise .

3. Méthode d’itération

La méthode d’itération est une méthode mathématique utilisée pour calculer des valeurs approximatives de Pi. Cette méthode utilise une formule qui implique la valeur de Pi et est appliquée de manière itérative pour améliorer la précision du calcul. Voici les étapes pour utiliser cette méthode :

Choisissez une valeur initiale pour Pi. Par exemple, vous pouvez choisir la valeur 3.
Utilisez une formule impliquant la valeur de Pi pour calculer une nouvelle valeur approximative. Par exemple, vous pouvez utiliser la formule suivante : Pi = (Pi + (4 ÷ Pi)) ÷ 2
Compare la nouvelle valeur approximative avec l’ancienne valeur. Si la différence entre les deux est assez petite, alors vous êtes arrivé à un résultat précis. Si la différence est encore importante, attribuez la nouvelle valeur à Pi et répétez le processus à partir de l’étape 2.

Par exemple, si la valeur initiale de Pi est 3, la nouvelle valeur approximative serait (3 + (4 ÷ 3)) ÷ 2 = 2,66666666. Mais, comme la différence entre les deux n’est pas très petite , vous pouvez toujours répéter le processus plusieurs fois avant de trouver une valeur précise.

Quelles sont les applications du nombre Pi ?

Pi est un nombre important en mathématiques et a de nombreuses applications dans divers domaines. Parmi les applications les plus importantes de Pi, nous avons les suivantes :

Géométrie

Pi est utilisé en géométrie pour calculer l’aire et le périmètre des cercles et autres figures circulaires :

Cercles : Calculez l’aire et le périmètre des cercles.
Sphères : déterminer l’aire et le volume des sphères.
Cylindres : Calcul de la surface et du volume des cylindres.
Cônes – Utilisé pour calculer la surface et le volume des cônes.

Trigonométrie

Il est utile en trigonométrie pour calculer les angles et les longueurs d’arc. Certaines de ses applications sont :

Angles : calcul des angles et des longueurs d’arcs.
Fonctions trigonométriques – Utilisées pour calculer la valeur des fonctions trigonométriques pour certains angles.
Trigonométrie circulaire : pour calculer les valeurs des fonctions trigonométriques pour des angles de 360 degrés.

Ingénierie

En ingénierie, Pi est utilisé dans le calcul de quantités telles que le volume et la capacité. Certaines de ses applications sont :

Électronique : calculer des grandeurs telles que la résistance et la capacité.
Electricité : elle sert à calculer des grandeurs telles que la puissance et l’énergie électrique.
Génie civil : calculer des grandeurs telles que la surface et le volume des structures et des éléments de construction.

Physique

Le nombre Pi (π) est une constante mathématique qui a de nombreuses applications en physique. Voici quelques exemples d’utilisation de Pi en physique :

Ondes – Utilisé pour calculer la fréquence et la longueur d’onde des ondes.
Mécanique : En mécanique, il est utile pour calculer le travail et l’énergie dans les systèmes tournants.
Électromagnétisme : En électromagnétisme, il peut être utilisé pour calculer l’énergie stockée dans un condensateur et l’inductance dans un enroulement.
Cosmologie En cosmologie, Pi est utilisé pour calculer la courbure de l’espace-temps et l’expansion de l’univers.

Quelles applications le nombre Pi a-t-il dans la vraie vie ?

Voici quelques exemples d’utilisation de Pi dans la vie quotidienne :

Géométrie : pour définir la surface d’un tapis circulaire ou pour mesurer la longueur du mètre ruban nécessaire pour couvrir le périmètre d’une table circulaire.
Cuisson – déterminer la quantité d’eau ou de liquide nécessaire pour remplir une casserole ou le nombre d’ingrédients pouvant tenir dans un récipient circulaire.
Astronomie : connaître la distance entre les planètes et les étoiles, l’orbite des planètes, et la position des corps célestes dans le ciel.
Jardinage : connaître la quantité de terre ou de sol nécessaire pour remplir un pot circulaire ou pour calculer la quantité d’eau nécessaire pour arroser une plante dans un jardin circulaire.