La formule d’Euler est un concept mathématique qui relie deux concepts élémentaires des mathématiques : les nombres complexes et la trigonométrie. Cela en fait l’une des conceptualisations les plus importantes et avec le plus d’applications dans toutes les mathématiques. Tout au long de cet article, nous verrons à quoi ressemble cette formule et toutes les utilisations dont elle dispose.
Quelle est la formule d’Euler ?
La formule d’Euler est une équation mathématique fondamentale basée sur le nombre d’Euler , qui relie les nombres complexes à la trigonométrie. Il a été découvert par le mathématicien suisse Leonhard Euler au 18ème siècle et a depuis été utilisé dans une variété de domaines, de la physique à l’informatique.
La formule d’Euler s’écrit e ix = cos(x) + i sin(x) , où e est la base du logarithme naturel, i est l’ unité imaginaire (définie comme la racine carrée de -1) et x est un nombre réel. Cette équation précise que le nombre complexe e ix est égal à la somme du nombre réel cos(x) et du produit du nombre imaginaire i par le nombre réel sin(x).

L’importance de la formule d’Euler réside dans le fait qu’elle permet d’exprimer les nombres complexes en termes de nombres réels et de trigonométrie, ce qui facilite leur manipulation et leur calcul.
Preuve de la formule d’Euler
La preuve de la formule d’Euler est basée sur l’utilisation de la série de Taylor pour la fonction exponentielle et l’identité trigonométrique pour le cosinus et le sinus.
Premièrement, nous considérons la série de Taylor pour la fonction exponentielle :

Ensuite, on remplace x par ix dans l’équation ci-dessus, où i est l’unité imaginaire (racine carrée de -1) :
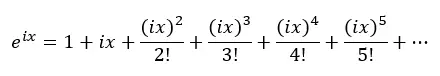
Donc, nous appliquons les puissances de i et remplaçons dans l’équation précédente :
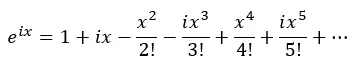
Maintenant, nous regroupons les termes réels et les termes avec i :
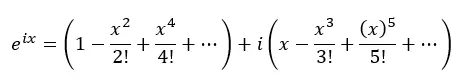
En fait, chacune des parenthèses ci-dessus est la série de Taylor pour le cosinus et le sinus :
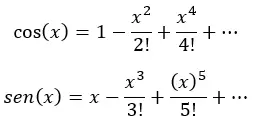
Enfin, on simplifie (en remplaçant chaque expression entre parenthèses par cosinus et sinus de x) et on obtient :

Exemple de formule d’Euler
Maintenant que vous savez comment fonctionne cette formule mathématique, nous vous recommandons d’essayer de résoudre l’exemple pratique suivant : Exprimez le nombre complexe e 2i (en radians) sous forme binomiale :
L’application principale de la formule d’Euler est de convertir un nombre complexe exprimé sous forme exponentielle, en forme binomiale. Nous allons donc utiliser la formule : e ix = cos(x) + i sin(x)
e 2i = cos(2) + je sin(2)
e2i = -0,416 + 0,909i
Et nous aurions déjà le nombre sous forme binomiale. De là, nous pouvons faire la représentation graphique dans le plan complexe . Pour ce faire, il faut comprendre qu’un nombre complexe est représenté dans le plan complexe en utilisant comme coordonnées la partie réelle en abscisses (axe des abscisses) et la partie imaginaire en ordonnées (axe des ordonnées).
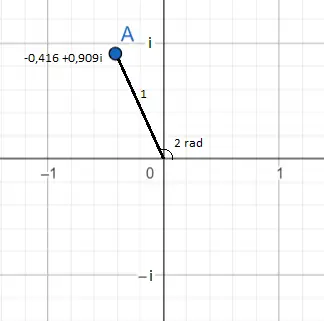
Dans l’image précédente, le nombre complexe e 2i est représenté, qui est égal à -0,416 + 0,909i. Cela peut être vu comme un point de couleur bleue. On peut voir son emplacement sur l’avion sous deux angles .
La première et la plus évidente est avec la représentation du nombre sous forme binomiale : -0.416 (en abscisse) et 0.909 (en ordonnée). Et le second est de la forme exponentielle : le module de e 2i est égal à 1, car c’est le nombre qui est devant le e (puisqu’il n’y a pas de nombre devant e, il faut imaginer qu’il y a un 1) et dans l’exposant il y a un 2, donc, l’argument ou l’angle équivaut à deux radians.
Si vous ne comprenez pas bien ce dernier paragraphe , nous vous recommandons de lire notre article sur les nombres complexes. Eh bien, nous y faisons une explication très approfondie des différentes manières d’écrire un nombre complexe et de toutes ses propriétés.
Représentation graphique de la formule d’Euler
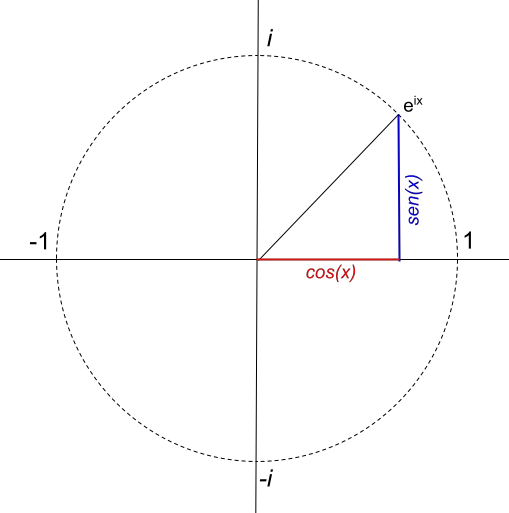
Dans l’exemple précédent, vous avez pu voir comment la formule d’Euler est appliquée et comment elle est représentée graphiquement dans le plan complexe. Mais, si on va un peu plus loin et qu’on essaie de représenter une fonction équivalente à la formule d’Euler, on trouve quelque chose de très curieux : elle génère un cercle de rayon 1 :
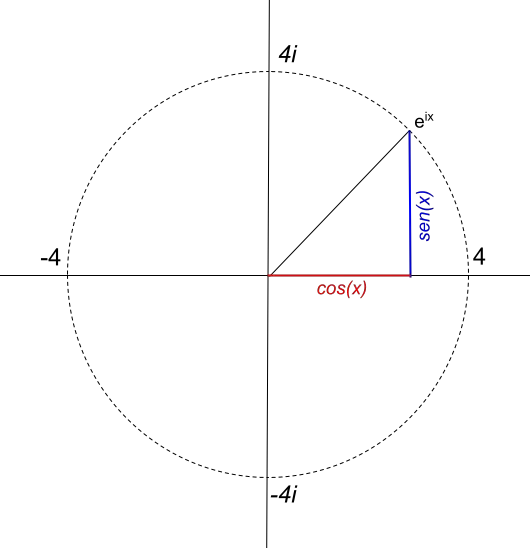
Cependant, le rayon du cercle dépend directement de la valeur du module du nombre complexe. Par exemple, si nous voulons représenter un cercle de rayon 4, la fonction sera 4e ix . Ainsi, la fonction 4e ix , est représentée comme ceci :
Revenant au cercle de rayon 1, si on décide de représenter e iπ (en radians), il faut d’abord calculer :
e πi = cos(π) + je sin(π)
eπi = -1 + je 0
eπi = -1
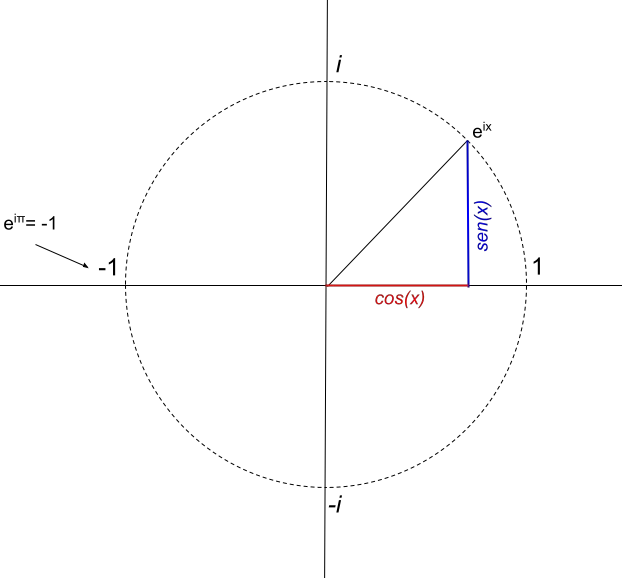
On obtient e πi = -1, qui est la fameuse identité d’Euler.
On en déduit que le nombre complexe e πi n’a qu’une partie réelle, qui est égale à -1. Par conséquent, sa représentation serait telle que :
Applications de la formule d’Euler
- Nombres complexes : La formule d’Euler est une relation entre les fonctions trigonométriques et les nombres complexes. A partir de cette formule, nous pouvons exprimer les nombres complexes de différentes manières : binomiale, exponentielle et polaire.
- Série de Taylor : la formule d’Euler est utilisée pour étendre les fonctions en série de Taylor.
- Algèbre linéaire : La formule d’Euler est utilisée dans la diagonalisation matricielle, qui est une technique fondamentale en algèbre linéaire.
- Calcul différentiel et intégral : La formule d’Euler est utilisée dans la solution des équations différentielles, qui est une technique pertinente en calcul.
De plus, il a des applications dans de nombreuses théories mathématiques et même dans des concepts extérieurs au domaine mathématique, tels que les théorèmes de physique.
conclusions
Comme vous avez pu le voir dans cet article, la plus grande application de la formule d’Euler est dans les nombres complexes : dans son expression numérique et dans sa représentation. Il est vrai que cela a une certaine application en algèbre, mais essentiellement, vous travaillez avec des nombres complexes. Il est donc important de bien les comprendre avant tout.
Cela étant dit, nous espérons vous avoir aidé à mieux comprendre ce concept. Et si vous avez des questions ou ne savez pas comment procéder à un exercice, n’hésitez pas à nous écrire dans les commentaires.