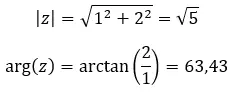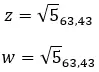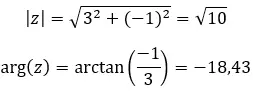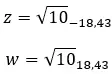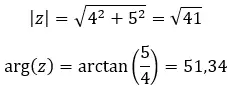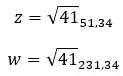Dans cet article, nous allons traiter des propriétés des nombres complexes , qui peuvent être utiles lors de la résolution de calculs et de la simplification d’expressions. Allons directement voir ces propriétés.
Module et argument d’un nombre complexe
La première propriété d’un nombre complexe est le module et l’argument d’un nombre complexe. C’est très facile à calculer, car il suffit d’appliquer quelques formules.
La formule pour calculer le module :

La formule pour calculer l’argument :

Maintenant, si le nombre est exprimé sous forme polaire ou trigonométrique, il n’est pas nécessaire de faire de calculs. Parce que, dans la même expression, le module et l’argument sont répertoriés.
Dans l’image ci-dessous, vous pouvez voir la formule d’un nombre sous forme polaire, où |z| est le module et α est l’argument.

Et dans cette autre image, vous pouvez voir la structure d’un nombre exprimé sous forme trigonométrique, où |z| est le module et α est l’argument.

nombres complexes égaux
Les nombres complexes égaux sont ceux qui partagent le module et l’argument. Donc, à partir de ces deux valeurs :

Ce sont les mêmes si la propriété suivante est remplie.
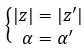
D’un autre côté, si nous avons les deux nombres sous forme binomiale, nous pouvons faire une vérification très rapide et facile pour voir s’il s’agit de deux nombres complexes égaux. Simplement, l’expression suivante doit être remplie :
un + bi = un + bi
Voyons un exemple, déterminez si les deux nombres complexes suivants sont égaux :
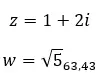
Conjuguer les nombres complexes
Passons maintenant à l’une des propriétés les plus importantes des nombres complexes, car savoir calculer le conjugué d’un complexe nous aide beaucoup à résoudre des divisions complexes et à faire des simplifications.
Donc, à partir de ces deux valeurs :

On dit qu’ils sont conjugués s’ils partagent un module et ont des arguments opposés. Il doit donc être rempli :
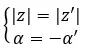
D’un autre côté, si nous avons les deux nombres sous forme binomiale, nous pouvons faire une vérification très rapide et facile pour voir s’il s’agit de deux nombres conjugués complexes. Simplement, l’expression suivante doit être remplie :
un + bi = un – bi
Voyons un exemple, déterminez si les deux nombres complexes suivants sont conjugués :
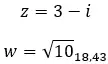
Nombres complexes opposés
Ensuite, nous passons à voir la propriété des nombres complexes opposés. A partir de ces deux valeurs :

On peut dire qu’ils sont opposés s’ils ont le même module et que leurs arguments diffèrent de 180 degrés ou π radians :
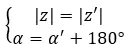
D’autre part, si nous avons les deux nombres sous forme binomiale, nous pouvons utiliser une autre méthode encore plus rapide et plus simple pour savoir s’il s’agit de deux nombres complexes opposés. Simplement, l’expression suivante doit être remplie :
un + bi = -a – bi
Voyons un exemple, déterminez si les deux nombres complexes suivants sont opposés :
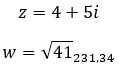
autres propriétés
Évidemment, cet ensemble numérique a d’autres propriétés, telles que les nombres complexes inverses et quelques autres qui sont directement liées aux opérations arithmétiques de base. Bien que tous ces éléments soient abordés dans d’autres articles, que vous pouvez voir dans la liste ci-dessous.