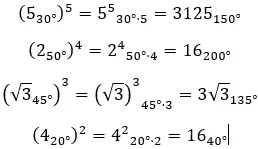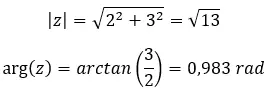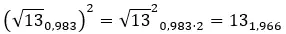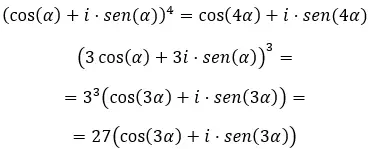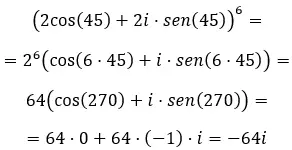Puissances des nombres complexes

Résoudre les puissances des nombres complexes est une chose assez facile à faire, si vous connaissez la bonne méthode. C’est pourquoi, dans cet article, nous expliquerons comment résoudre des puissances complexes de trois manières : pour les nombres complexes sous forme binomiale, sous forme polaire et sous forme trigonométrique.

Comment résoudre la puissance d’un nombre complexe ?

Comme nous l’avons dit dans l’introduction, trois situations peuvent se présenter lorsque l’on opère avec des puissances complexes. La première et la plus simple est quand on nous donne le nombre sous forme polaire . La seconde est quand on nous donne le nombre sous forme binomiale et la troisième est quand on nous donne le nombre sous forme trigonométrique.

En d’autres termes, lorsque l’on opère avec des complexes sous forme polaire, l’exercice peut être résolu plus rapidement. Par conséquent, il est recommandé de convertir le nombre en question en forme polaire. Mais en fait, toutes les méthodes sont faciles à résoudre . Cela dit, nous allons vous expliquer comment se résolvent tous les cas et nous vous proposerons un exercice.

Puissances des nombres complexes sous forme polaire

Quand on veut résoudre des puissances complexes sous forme polaire , il suffit d’élever le module à any et de multiplier l’argument par n. Exprimé mathématiquement, on obtient la formule suivante :

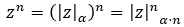
Voici quelques exemples, afin que vous puissiez essayer de les résoudre par vous-même :

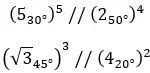
Puissances des nombres complexes sous forme binomiale

En revanche, lorsque l’on veut résoudre des puissances complexes sous forme binomiale , on peut recourir à deux méthodes différentes. La première traite de la résolution de la puissance de manière “algébrique” (résolution comme si i était une variable). Et le deuxième système consiste à convertir la forme binomiale en polaire, puis à suivre la procédure d’avant.

Si vous ne savez pas comment passer du binôme à la forme polaire, nous vous l’expliquons très clairement dans notre article sur les nombres complexes . Bien que, maintenant, nous allons le voir rapidement avec un exemple.

Essayez de résoudre la puissance complexe suivante : (2 + 3i) ² .

Puissances des nombres complexes sous forme trigonométrique

Enfin, lorsque l’on veut résoudre des puissances complexes sous forme trigonométrique , il faut utiliser la formule bien connue de de Moivre. Qui s’écrit comme suit :

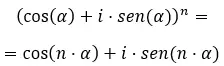
Connaissant cette formule, essayez de résoudre les exercices suivants :

En savoir plus sur les pouvoirs complexes

• Nombres complexes
• Propriétés des complexes
• Opérations sur les nombres complexes
• racines complexes