Fonction irrationnelle ou fonction radicale -

Cette page explique ce qu’est une fonction irrationnelle, aussi appelée fonction radicale, ainsi que toutes les caractéristiques de ce type de fonction. Vous découvrirez également comment calculer le domaine des fonctions radicales ou irrationnelles et, en plus, vous pourrez voir comment les représenter sur un graphique avec des exemples et de la pratique avec des exercices et des problèmes résolus étape par étape.

Qu’est-ce qu’une fonction irrationnelle (ou radicale) ?

Une fonction irrationnelle signifie la même chose qu’une fonction radicale et, par conséquent, elles partagent une définition :

Une fonction irrationnelle , également appelée fonction radicale , est une fonction qui a la variable indépendante x sous le symbole d’une racine.

Comme nous le savons déjà, le résultat d’une racine peut être positif ou négatif. Ainsi la représentation d’une fonction irrationnelle (ou radicale) a deux courbes possibles :

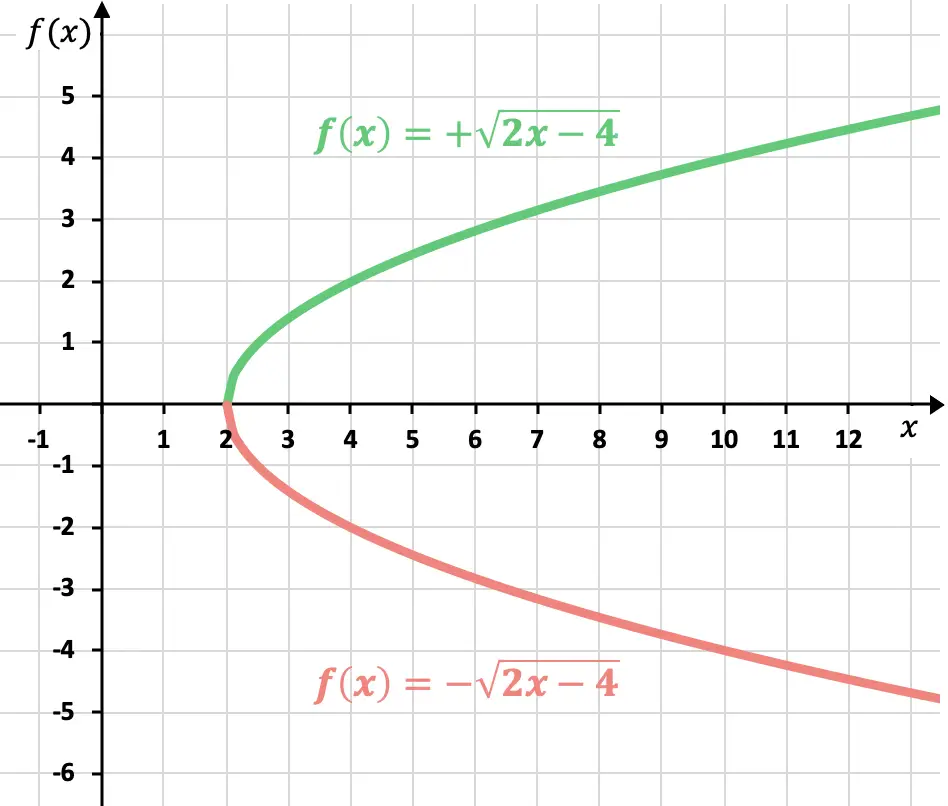
exemples de fonctions irrationnelles ou radicales

Mais si le signe n’est pas précisé, la fonction positive est censée être représentée.

En revanche, il ne faut pas confondre une fonction irrationnelle avec une fonction rationnelle. Bien qu’elles portent des noms très similaires, il s’agit de deux types de fonctions totalement différents.

Domaine d’une fonction irrationnelle ou radicale

Le domaine d’une fonction avec des racines dépend de la parité de l’indice racine, c’est-à-dire qu’il dépend du fait que l’indice radical soit pair ou impair.

Domaine d’une fonction avec racine d’index pair

Comme vous le savez bien, il n’existe pas de racine (même d’index) d’un nombre négatif. Par conséquent, une fonction radicale avec un indice pair existera tant que son contenu est égal ou supérieur à 0.

A titre d’exemple, voyons comment est calculé le domaine de la fonction radicale ou irrationnelle suivante :

$f(x)=\sqrt{x-4}$

Il s’agit d’une fonction d’indice pair radical, il faut donc regarder quand son contenu est positif ou nul :

$x-4\ge 0$

On résout l’inégalité :

$x\ge 4$

Ainsi, la fonction existera chaque fois que x est supérieur ou égal à 4, et est indiquée par l’intervalle suivant :

$\text{Dom } f= [4,+\infty)$

Domaine d’une fonction avec racine d’index impair

Les fonctions irrationnelles avec un indice impair n’ont pas ce problème, puisque la racine d’indice impair d’un nombre négatif existe :

$\sqrt[3]{-8}=-2$

Par conséquent, des fonctions radicales d’indice impair existent pour toute valeur de x . Ou, en d’autres termes, le domaine est constitué uniquement de nombres réels .

Par exemple, nous allons calculer le domaine de définition de la fonction radicale suivante dont l’indice est impair :

$f(x)=\sqrt[3]{3x-4}$

Puisqu’il s’agit d’une fonction irrationnelle avec un indice impair, son domaine est constitué de nombres réels :

$\text{Dom } f= \mathbb{R}$

Comment représenter une fonction irrationnelle ou radicale

Voyons comment représenter une fonction avec des racines sur un graphique à l’aide d’un exemple.

Représenter la fonction radicale ou irrationnelle suivante sur un graphique :

$f(x)=\sqrt{x+2}$

La première chose à faire est de trouver le domaine de la fonction. Puisqu’il s’agit d’une racine carrée, ce qu’il contient doit être positif, puisqu’il n’y a pas de racine carrée d’un nombre négatif. Par conséquent, la fonction radicale existera tant que son contenu est égal ou supérieur à 0 :

$x+2\ge 0$

$x\ge -2$

Ainsi, le domaine de la fonction est constitué de tous les nombres supérieurs ou égaux à -2. C’est-à-dire:

$\text{Dom } f = [-2,+\infty)$

Une fois que nous connaissons le domaine de la fonction, nous créons une table de valeurs. Évidemment, plus nous calculons de points, plus la représentation de la fonction sera précise. Mais calculer 3 ou 4 points dans l’intervalle du domaine suffit :

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

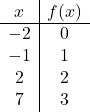
Nous représentons maintenant les points obtenus sur un graphique :

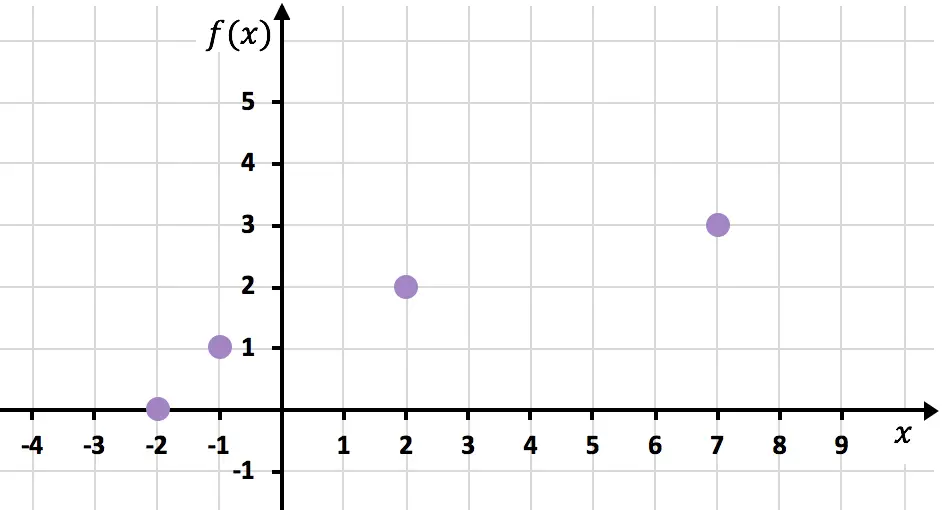
comment représenter une fonction radicale ou irrationnelle

Et enfin, nous joignons les points et allongeons la courbe pour indiquer que la fonction continue de croître :

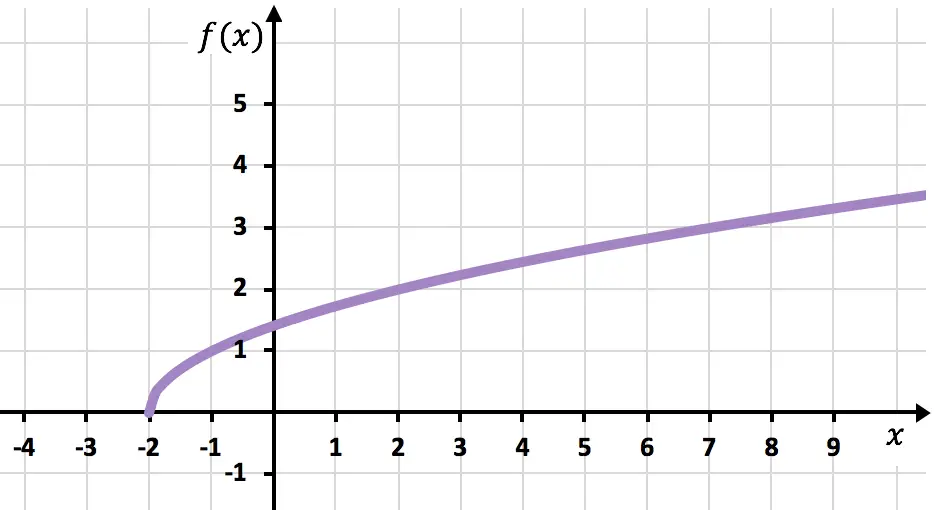
exemple de représentation graphique d'une fonction radicale ou irrationnelle

Exercices résolus sur les fonctions irrationnelles ou radicales

Exercice 1

Trouvez le domaine de la fonction radicale suivante :

$\sqrt{3x+6}$

Voir la solution

La racine carrée d’un nombre négatif n’existe pas. Par conséquent, la fonction existera lorsque l’argument racine est positif ou nul :

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Exercice 2

Trouvez le domaine de la fonction irrationnelle suivante :

$\sqrt{-x+2}$

Voir la solution

La racine carrée d’un nombre négatif n’a pas de véritable solution. Par conséquent, la fonction existera tant que le contenu de la racine est positif ou nul :

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

N’oubliez pas que si dans une inégalité nous changeons les côtés d’un nombre négatif qui se multiplie ou se divise, nous devons également faire pivoter le signe de l’inégalité.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Exercice 3

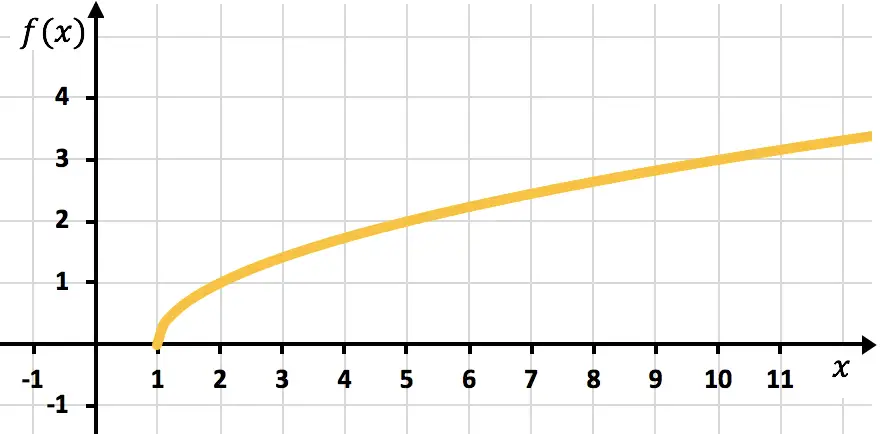
Représentez la fonction irrationnelle suivante sur un graphique :

$f(x)= \sqrt{x-1}$

Voir la solution

Tout d’abord, il faut calculer le domaine de la fonction :

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Maintenant, nous créons un tableau de valeurs en donnant les valeurs de la fonction dans la plage du domaine :

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Enfin, nous traçons les points et traçons la fonction sur le graphique :

exercice résolu étape par étape d'une fonction irrationnelle ou radicale

Exercice 4

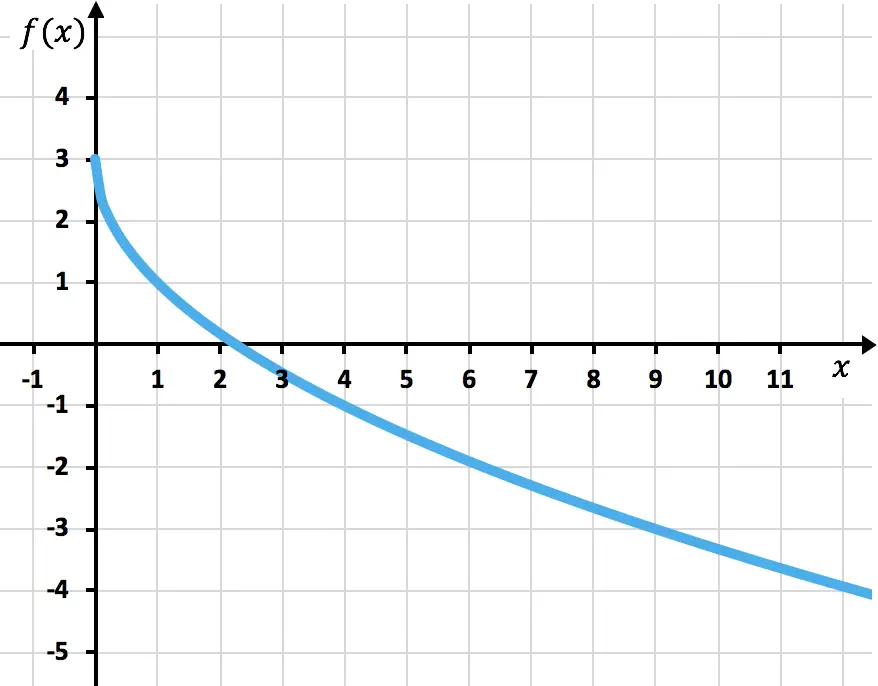
Représentez graphiquement la fonction irrationnelle ou radicale suivante :

$f(x)= -2\sqrt{x}+3$

Voir la solution

Tout d’abord, il faut calculer le domaine de la fonction :

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Maintenant, nous créons un tableau de valeurs en donnant les valeurs de la fonction dans la plage du domaine :

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Pour finir, nous représentons les points et dessinons la fonction sur le graphique :

Exercice 5

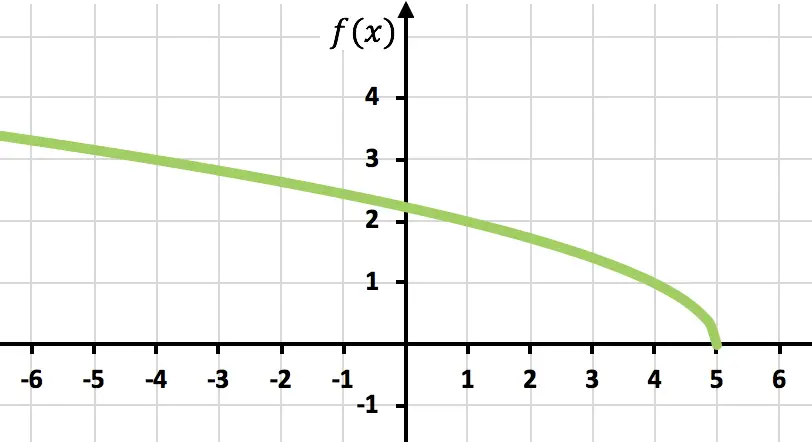
Faites la représentation graphique de la fonction irrationnelle ou radicale suivante :

$f(x)= \sqrt{-x+5}$

Voir la solution

Avant de tracer la fonction, nous devons calculer le domaine de la fonction :

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

N’oubliez pas que si dans une inégalité nous changeons les côtés d’un nombre négatif qui se multiplie ou se divise, nous devons également changer le signe de l’inégalité.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Maintenant, nous construisons un tableau de valeurs en évaluant la fonction en des points qui appartiennent au domaine de la fonction :

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

Et pour finir, il suffit de représenter les points et de peindre la fonction sur le graphique :

exercices résolus de fonctions radicales ou irrationnelles

Exercice 6

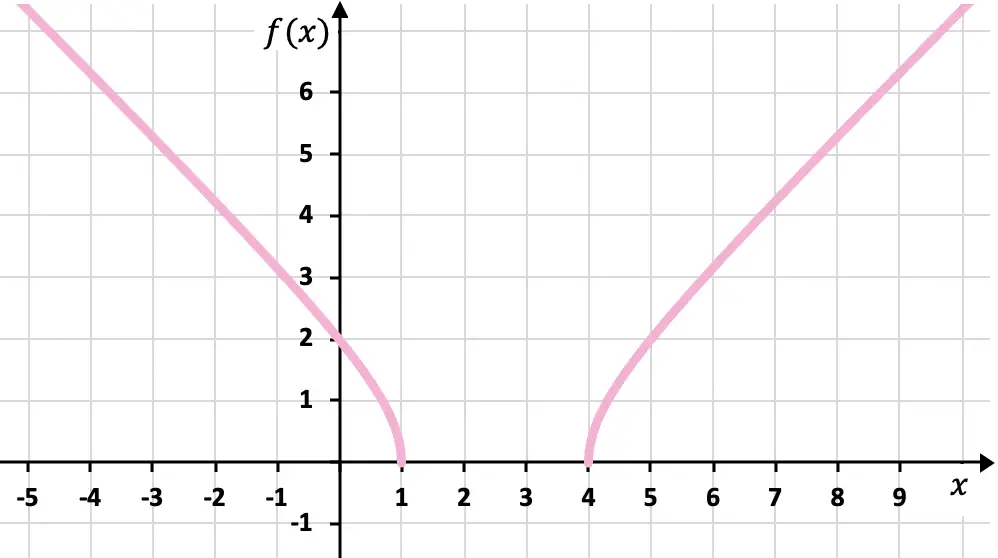
Représenter la fonction irrationnelle ou radicale suivante sur un graphique :

$f(x)= \sqrt{x^2-5x+4}$

Voir la solution

Il faut d’abord calculer le domaine de la fonction :

$x^2-5x+4\ge 0$

Dans ce cas, nous avons obtenu une inégalité du deuxième degré, nous devons donc appliquer la formule des équations du deuxième degré pour la résoudre :

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

On divise la ligne en trois morceaux avec les racines obtenues :

Et nous substituons un nombre à chaque section de l’inégalité, pour voir quelles sections satisfont à l’inégalité et, par conséquent, appartiennent au domaine :

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0$

❌

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$ $5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$ ✅

Ainsi, les sections qui respectent l’inégalité sont celles des côtés :

Le domaine de la fonction est donc :

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Une fois que nous avons calculé le domaine de la fonction, nous construisons un tableau de valeurs donnant les valeurs de la fonction dans l’intervalle du domaine :

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Enfin, nous représentons les points obtenus sur le graphique et traçons la fonction :

graphique d'une fonction irrationnelle ou radicale d'indice pair

Exercice 7

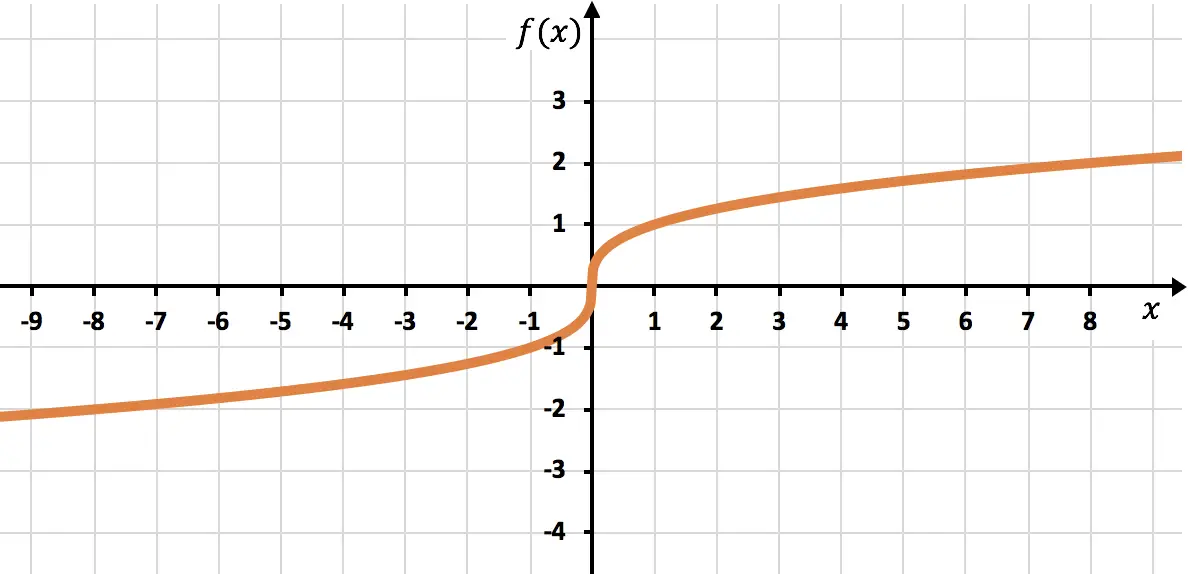
Représentez sur le graphique la fonction suivante formée par une racine :

$f(x)= \sqrt[3]{x}$

Voir la solution

C’est une fonction irrationnelle dont la racine a un indice impair, donc le domaine de la fonction est constitué de nombres réels :

$\text{Dom } f = \mathbb{R}$

On peut donc prendre n’importe quel point pour créer la table de valeurs. Dans ce cas nous chercherons de nombreux points car il s’agit d’une racine cubique :

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Enfin, nous représentons les points trouvés et traçons la fonction sur le graphique :

représenter graphiquement une fonction irrationnelle ou radicale avec un indice impair

Exercice 8

Résolvez le problème suivant lié aux fonctions irrationnelles (ou radicales) :

La consommation d’une batterie de téléphone portable est donnée par la fonction suivante :

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Où la consommation est exprimée en milliampères (mA) et

$t$ est le temps écoulé en minutes.

Déterminer la valeur de la constante

$K$ de sorte qu’au bout de 4 minutes la consommation est de 35 mA.

Voir la solution

Qu’après 4 minutes la consommation soit de 35 mA signifie que lorsque t vaut 4, f(t) vaut 35. Donc f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Nous devons maintenant résoudre l’équation que nous avons obtenue. Si vous regardez bien, c’est une équation irrationnelle puisqu’elle a une racine. Dans ce type d’équations, la première chose à faire est d’isoler la racine d’un côté, qui dans ce cas est déjà isolée. Une fois isolé, il faut mettre au carré les deux côtés de l’équation :

$\left( \sqrt{4-K} \right)^2= 35^2$