Cette page explique ce que sont les transformations de fonctions et comment les trouver. Il existe trois types de transformations : les traductions (ou déplacements), les symétries et les expansions (ou contractions). Vous trouverez également des exercices résolus étape par étape afin que vous puissiez pratiquer et comprendre les concepts sans laisser de doute.
Que sont les transformations de fonctions ?
Parfois, on peut nous demander de représenter graphiquement des fonctions élémentaires très similaires à d’autres que nous connaissons déjà. Eh bien, au lieu de représenter à nouveau la fonction similaire, des techniques peuvent être utilisées pour passer de la représentation d’une fonction à une autre facilement et rapidement.
Ainsi, les transformations de fonctions sont des techniques qui permettent de passer de la représentation graphique d’une fonction à la représentation graphique d’une autre fonction très similaire à travers des opérations élémentaires.
Fondamentalement, il existe trois types de transformations de fonctions élémentaires :
- Translations ou déplacements : une fonction peut être déplacée verticalement et horizontalement.
- Réflexions ou symétries : une fonction peut être réfléchie en utilisant l’axe X ou l’axe Y comme axe de symétrie.
- Expansions et compressions : une fonction peut être agrandie ou réduite.
Une fois que nous aurons vu le concept de transformation d’une fonction, nous allons approfondir chaque type de modification.
Translations ou déplacements de fonctions
Nous commencerons par les déplacements de fonction. Il en existe deux types : les traductions verticales et les traductions horizontales.
Translation ou déplacement vertical d’une fonction
Pour traduire ou déplacer une fonction verticalement (le long de l’axe Y), vous devez ajouter ou soustraire une constante à la fonction :
Nous déplaçons une fonction de k unités vers le haut en ajoutant ka à la fonction :
![]()
Nous décalons une fonction k unités vers le bas en soustrayant ka de la fonction :
![]()
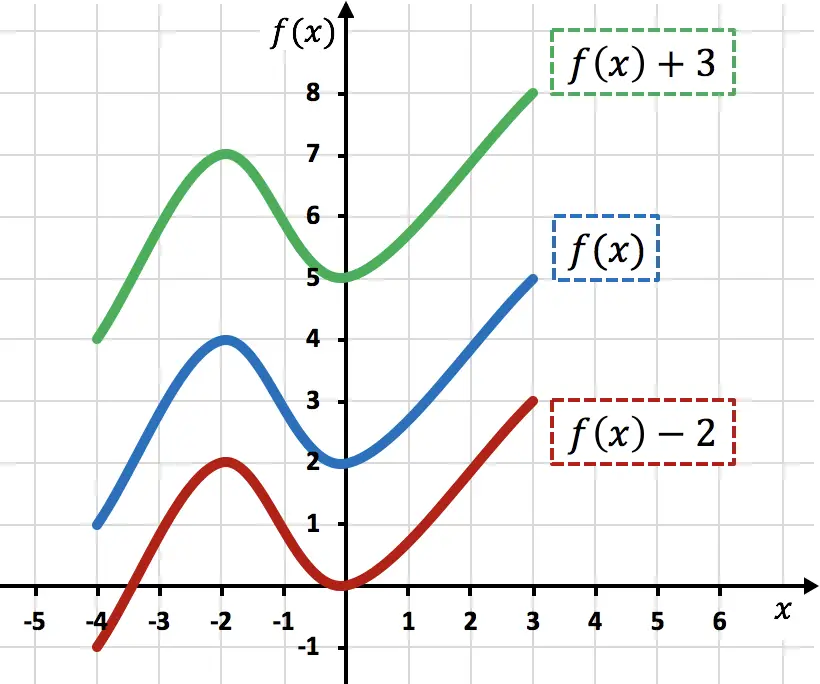
Comme vous pouvez le voir sur le graphique, l’ajout d’une constante à n’importe quelle fonction décale les unités ajoutées vers le haut (fonction verte). D’un autre côté, lors de la soustraction d’un nombre d’une fonction, les unités soustraites sont déplacées vers le bas (fonction rouge).
Notez que dans ce type de mouvements seules les coordonnées Y des points de fonction sont modifiées, tandis que les coordonnées X restent les mêmes.
Translation ou déplacement horizontal de fonctions
Pour traduire ou décaler une fonction horizontalement (le long de l’axe X) vous devez ajouter ou soustraire une constante à la variable indépendante x :
Le graphique de
![]() est le graphique de
est le graphique de![]() déplacé k unités vers la gauche.
déplacé k unités vers la gauche.
Le graphique de
![]() est le graphique de
est le graphique de![]() décalé k unités vers la droite.
décalé k unités vers la droite.
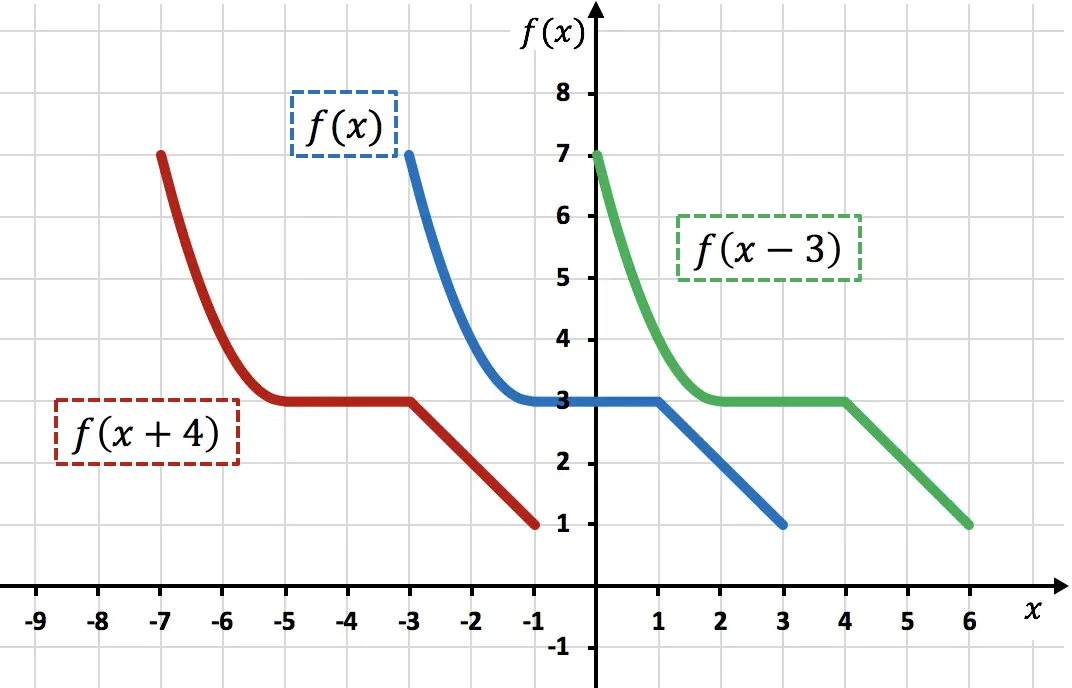
Comme vous pouvez le voir sur le graphique, lors de l’ajout d’une constante directement à la variable x , la fonction décale les unités ajoutées vers la gauche (fonction rouge). En revanche, lors de la soustraction d’un nombre à la variable x , la fonction décale les unités soustraites vers la droite (fonction verte).
Notez que dans ce type de mouvements, seules les coordonnées X des points de fonction sont modifiées, tandis que les coordonnées Y continuent avec la même valeur.
Exemple de traduction ou de déplacement d’une fonction
- Déplacez la fonction suivante de 4 unités vers le haut et de 3 unités vers la droite :
![]()
Pour déplacer la fonction de 4 unités vers le haut, nous devons ajouter 4 unités à la fonction :
![]()
Et pour déplacer également la fonction de 3 unités vers la droite il faut calculer
![]() . Par conséquent, là où il y a un
. Par conséquent, là où il y a un![]() nous mettons
nous mettons![]()
![]()
La fonction décalée de 4 unités vers le haut et de 3 unités vers la droite est donc :
![]()
Ci-dessous vous avez la fonction originale et la fonction transformée représentées graphiquement afin que vous puissiez voir la différence entre elles :
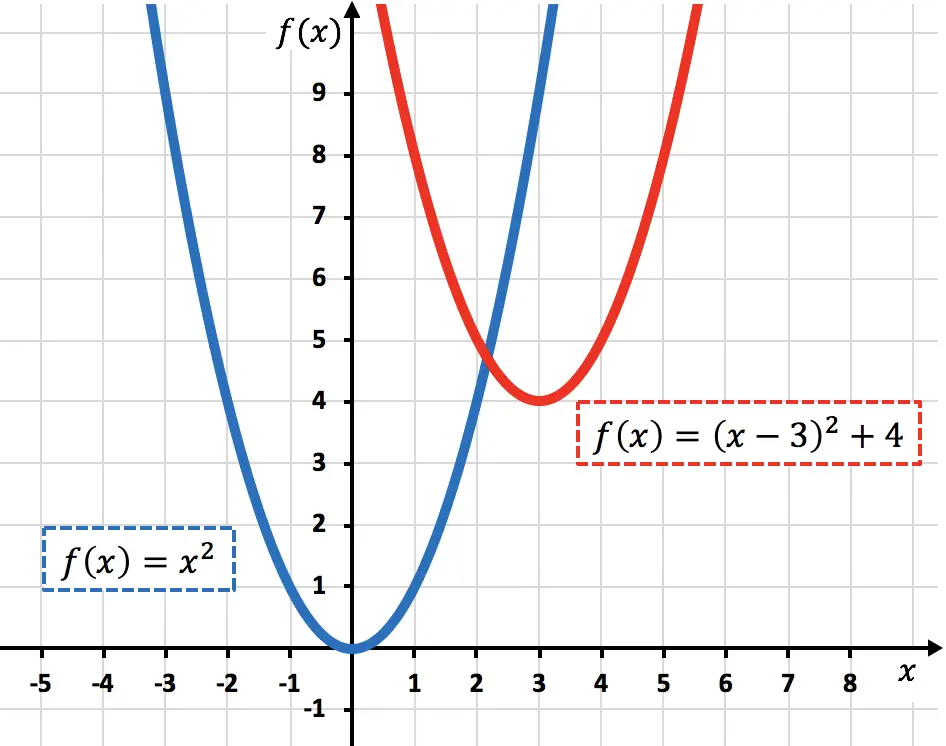
Certains mathématiciens appellent déplacement ou translation oblique lorsque les deux types de mouvements se produisent en même temps.
Réflexion ou symétrie d’une fonction par rapport aux axes de coordonnées
On peut représenter la fonction symétrique par rapport à n’importe quel axe cartésien de la manière suivante :
Pour refléter une fonction par rapport à l’axe des abscisses, nous devons changer le signe de la fonction, c’est-à-dire que nous devons calculer
![]()
Pour refléter une fonction par rapport à l’axe des ordonnées, nous devons nier la variable indépendante x , c’est-à-dire que nous devons calculer
![]()

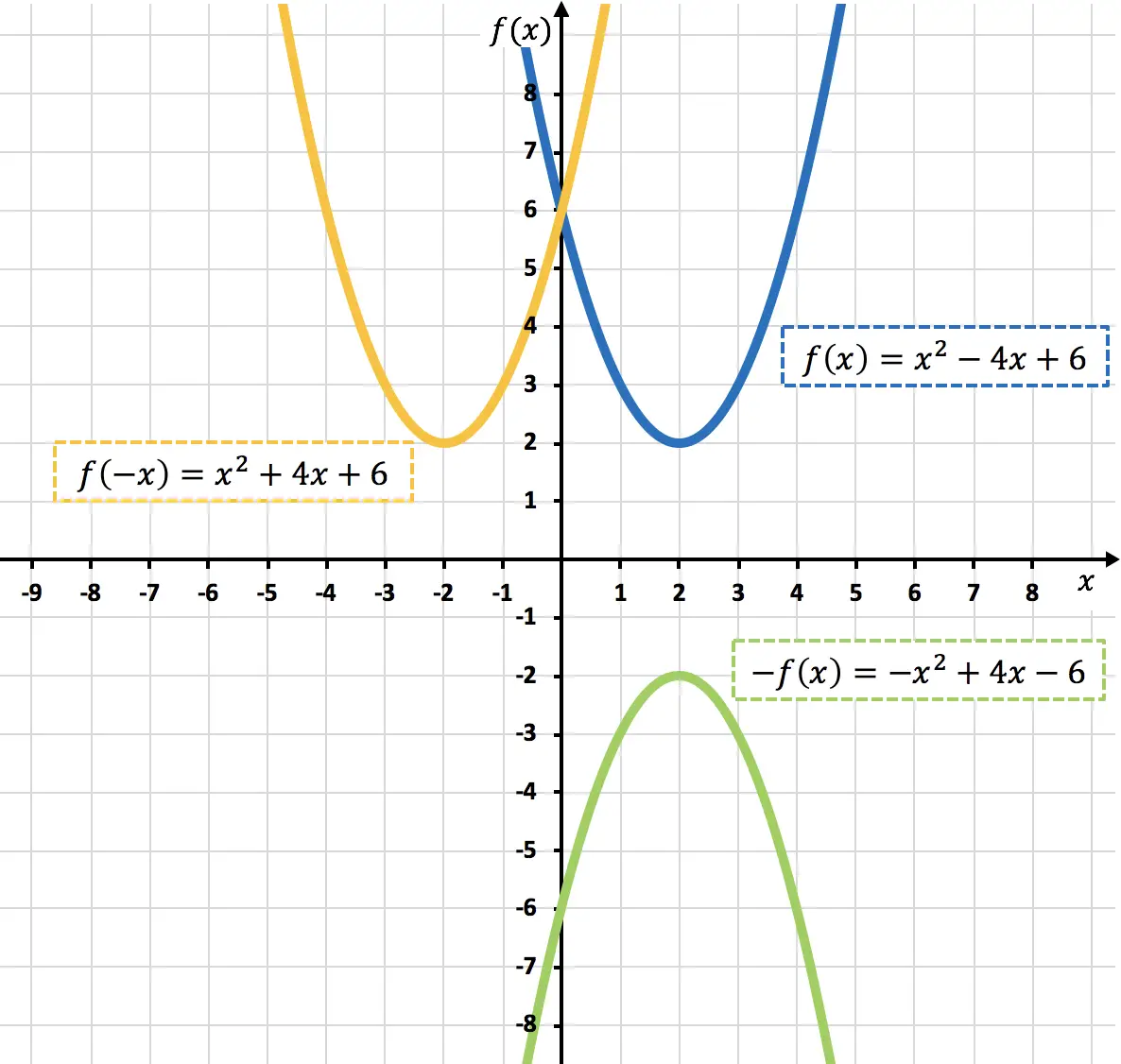
Comme vous pouvez le voir dans le graphique précédent, en multipliant une fonction par -1, nous l’inversons graphiquement (fonction orange), ou en d’autres termes, nous la reflétons par rapport à l’axe X.
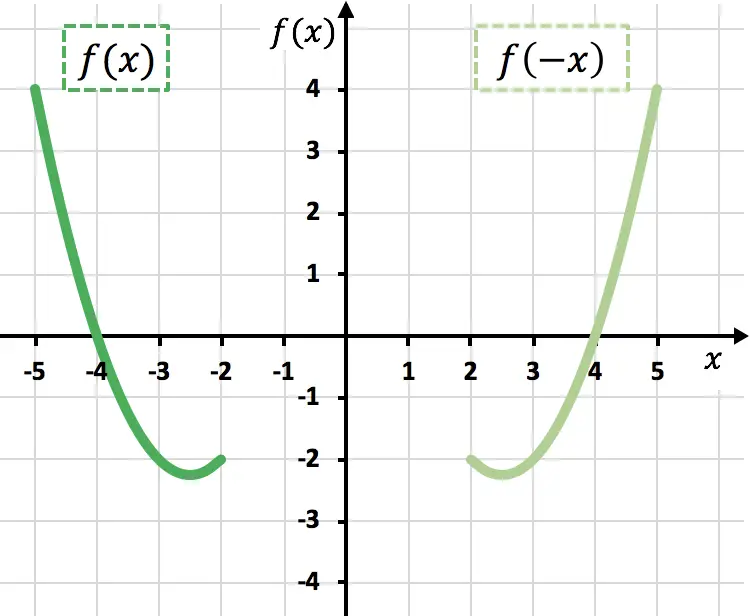
Comme on peut le voir dans le graphique précédent, en niant la variable x , nous reflétons la fonction par rapport à l’axe Y (fonction vert clair).
Exemple de mise en miroir d’une fonction
- Calculez la fonction symétrique par rapport à l’axe OX et la fonction symétrique par rapport à l’axe OY de la fonction quadratique suivante :
![]()
Pour trouver la fonction symétrique par rapport à l’axe X, il faut faire
![]() :
:
![]()
![]()
Et pour trouver la fonction symétrique par rapport à l’axe Y il faut faire
![]() . Par conséquent, nous remplaçons là où il y a un
. Par conséquent, nous remplaçons là où il y a un![]() dans la fonction originale par le terme
dans la fonction originale par le terme ![]()
![]()
![]()
![]()
![]()
Ci-dessous, vous avez représenté à la fois la fonction originale et les fonctions symétriques trouvées :
Expansions et contractions de fonctions
Comme pour les traductions, il existe deux types d’expansions ou de contractions : verticales et horizontales.
Expansion et contraction verticales d’une fonction
En multipliant une fonction entière par un coefficient, nous pouvons la faire se dilater ou se contracter :
Pour développer (ou dilater) une fonction sur l’axe Y, nous devons la multiplier par un nombre supérieur à 1 :
![]()
Pour réduire une fonction sur l’axe Y, nous devons la multiplier par un nombre positif inférieur à 1 :
 f(kx)\qquad 0
f(kx)\qquad 0
Pour réduire une fonction sur l’axe X, nous devons multiplier tous les x par un nombre supérieur à 1 :
![]()
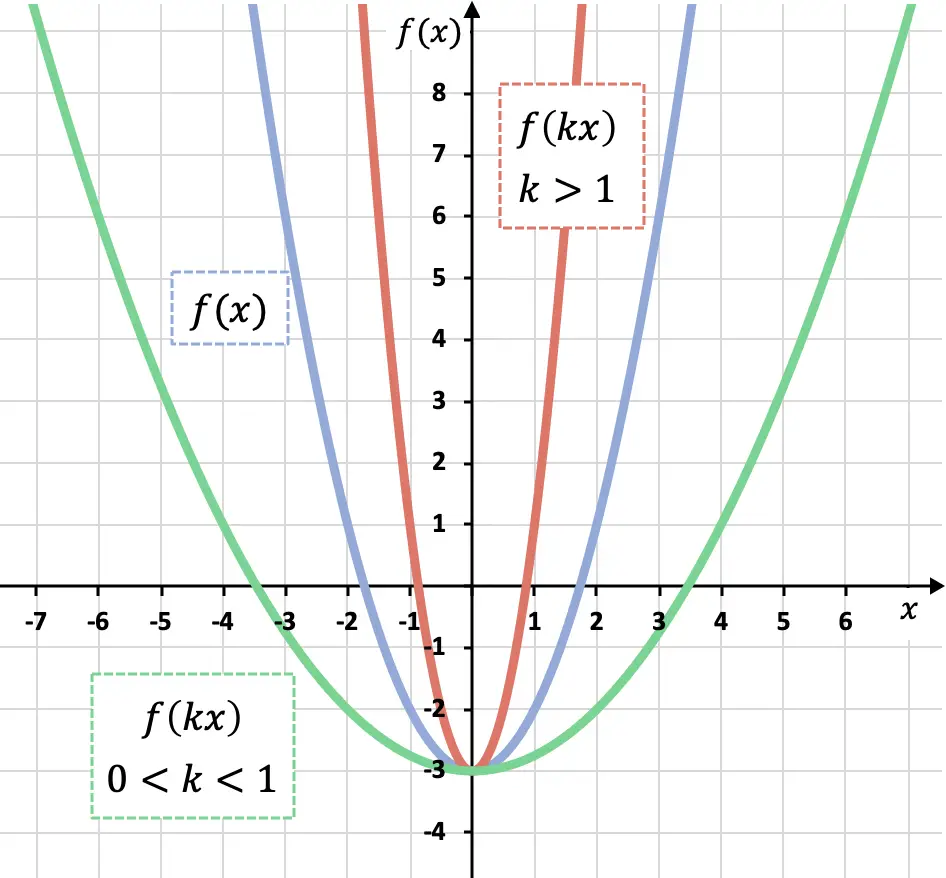
Comme vous pouvez le voir dans le graphique précédent, si on multiplie tous les x d’une fonction par un coefficient supérieur à 0 mais inférieur à 1 (fonction verte) on l’agrandit le long de l’axe OX, par contre, si nous multiplions une fonction par un coefficient supérieur à 1 (fonction rouge) nous la réduisons le long de l’axe OX.
Exemple de comment développer ou réduire une fonction
- Dupliquez verticalement et horizontalement la fonction irrationnelle suivante :
![]()
Pour étendre la fonction sur l’axe des ordonnées par deux, il faut multiplier la fonction entière par 2 :
![]()
Et pour développer également la fonction par deux sur l’axe des abscisses, il faut multiplier tous les x de la fonction par
![]()
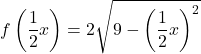
La fonction dupliquée sur les deux axes de coordonnées est donc :
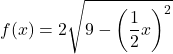
Ci-dessous vous avez la fonction originale et celle transformée représentée graphiquement afin que vous puissiez voir les différences entre elles :
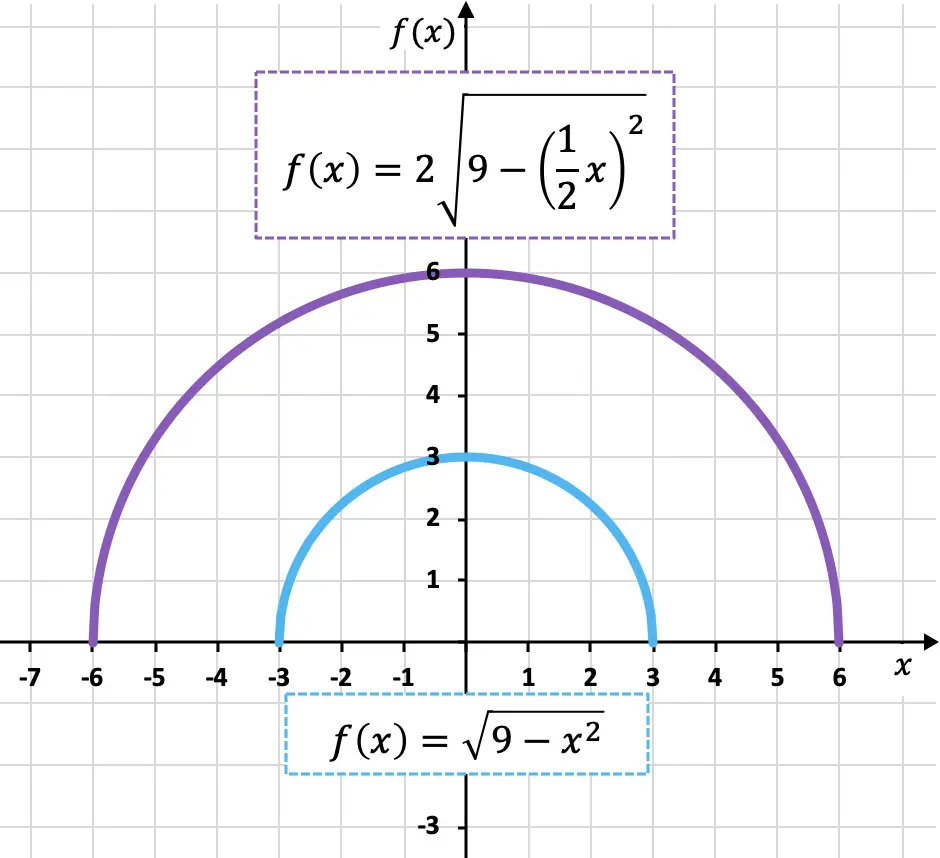
Comme vous pouvez le voir, la nouvelle fonctionnalité (couleur violette) est deux fois plus grande que la fonctionnalité d’origine (couleur bleue) à la fois verticalement et horizontalement, par conséquent, la fonctionnalité s’est étendue.
Exercices résolus sur les transformations de fonctions
Exercice 1
Déplacez la fonction de troisième degré suivante vers le haut de 5 unités :
![]()
Pour déplacer la fonction de 5 unités vers le haut, il faut ajouter 5 à la fonction :
![Rendered by QuickLaTeX.com \begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png)
La fonction décalée de 5 unités est donc :
![]()
Exercice 2
Trouvez la fonction symétrique par rapport à l’axe Y de la fonction quadratique suivante :
![]()
Pour trouver la fonction symétrique par rapport à l’axe Y il faut calculer
![]() , c’est-à-dire que nous devons remplacer
, c’est-à-dire que nous devons remplacer![]() pour
pour![]() dans la fonction :
dans la fonction :
![]()
![]()
La fonction symétrique par rapport à l’axe OY est donc :
![]()
Exercice 3
Effectuez une compression horizontale de la fonction suivante au tiers de sa représentation :
![]()
Pour réduire une fonction à travers le
![]()
![]()
![]()
La fonction réduite est donc :
![]()
Exercice 4
Calculez la fonction symétrique par rapport à l’axe OX de la fonction suivante translatée de 4 unités vers la droite :
![]()
Avant de calculer la fonction symétrique, il faut d’abord déplacer la fonction de 4 unités vers la droite, donc :
![]()
![]()
![]()
Et une fois qu’on a déplacé la fonction, on calcule la fonction symétrique par rapport à l’axe X. Pour ce faire, il faut nier la fonction obtenue :
![]()
![]()
En bref, la fonction après avoir appliqué toutes les opérations élémentaires est :
![]()
Exercice 5
Décalez la fonction suivante de 2 unités vers la gauche, puis développez-la verticalement d’un facteur 4 :
![]()
Tout d’abord, nous déplaçons la fonction de deux unités vers la gauche :
![]()
![]()
![]()
Et puis nous développons la fonction le long de l’axe Y avec un facteur 4 :
![]()
![]()
En conclusion, la fonction après avoir appliqué toutes les transformations élémentaires est :
![]()
Exercice 6
De la fonction
![]() détermine laquelle des représentations sur le graphique correspond à la fonction
détermine laquelle des représentations sur le graphique correspond à la fonction ![]()
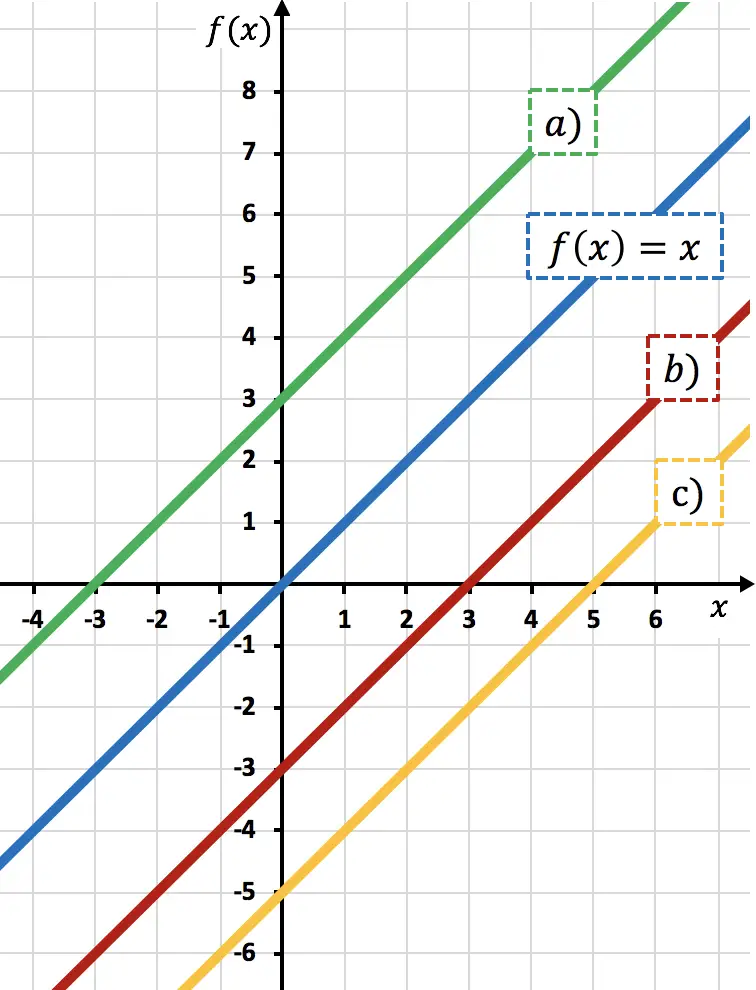
La fonction
![]() est la fonction
est la fonction![]() déplacé 3 unités vers le bas. Car en soustrayant un nombre d’une fonction, vous déplacez la fonction vers le bas.
déplacé 3 unités vers le bas. Car en soustrayant un nombre d’une fonction, vous déplacez la fonction vers le bas.
Par conséquent, la représentation de
![]() correspond à la droite b) , car elle est décalée de 3 unités vers le bas par rapport à
correspond à la droite b) , car elle est décalée de 3 unités vers le bas par rapport à![]()
Cela peut être vu en regardant l’axe vertical : quand
![]() passe par 0, la ligne rouge passe par -3, elle est donc décalée de 3 unités vers le bas.
passe par 0, la ligne rouge passe par -3, elle est donc décalée de 3 unités vers le bas.
Exercice 7
De la fonction
![]() déterminer quelle parabole est la représentation de la fonction
déterminer quelle parabole est la représentation de la fonction ![]()
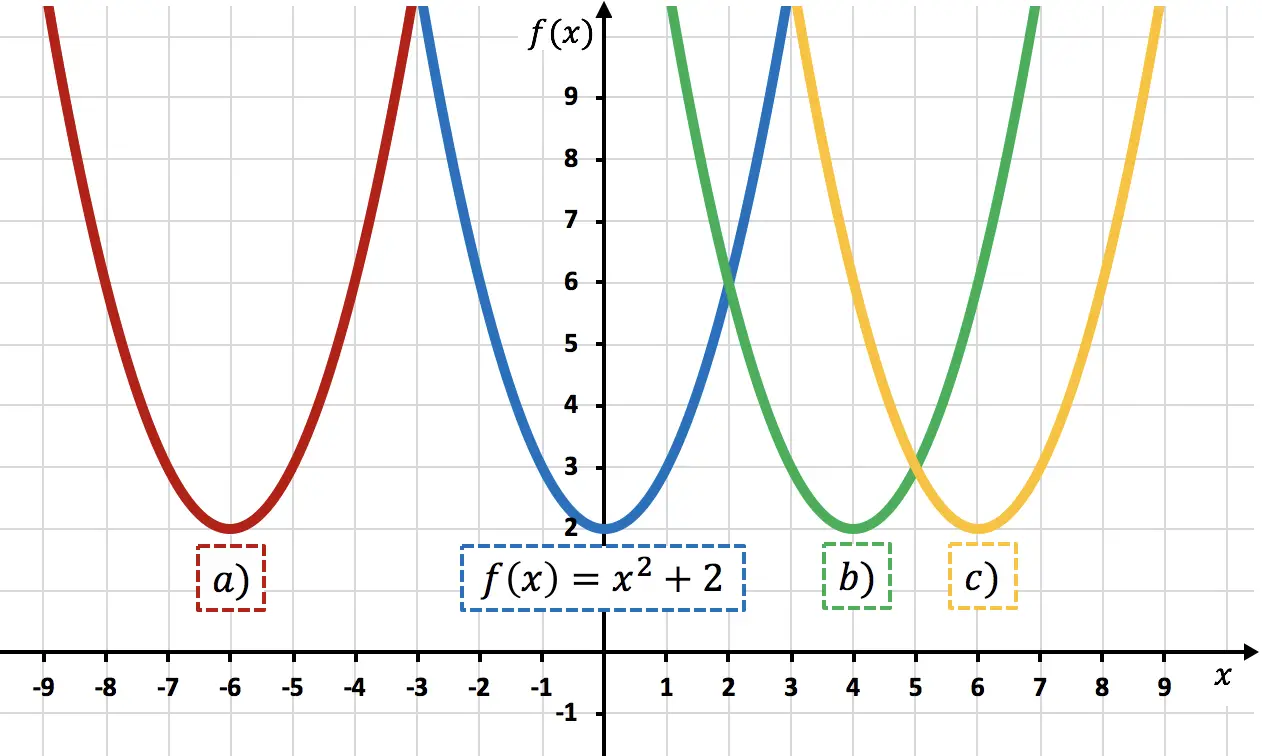
La fonction
![]() est la fonction
est la fonction![]() déplacé 6 unités vers la droite. Nous pouvons le vérifier en calculant
déplacé 6 unités vers la droite. Nous pouvons le vérifier en calculant ![]()
![]()
![]()
Par conséquent, la représentation de
![]() correspond à la parabole c) , car elle est décalée de 6 unités vers la droite par rapport à
correspond à la parabole c) , car elle est décalée de 6 unités vers la droite par rapport à![]() .
.
Cela peut être vu en regardant les sommets des paraboles : la distance entre le sommet de la parabole
![]() et le sommet de la parabole c) est de 6 unités, donc cette dernière est décalée de 6 unités vers la droite par rapport à la première.
et le sommet de la parabole c) est de 6 unités, donc cette dernière est décalée de 6 unités vers la droite par rapport à la première.