Dans cet article, vous découvrirez comment dériver l’arctangente d’une fonction. De plus, vous pourrez voir des exemples de ce type de dérivées et même vous entraîner avec des exercices résolus sur la dérivée de l’arctangente. Enfin, nous vous montrons également la preuve de la formule de la dérivée de l’arctangente.
Quelle est la dérivée de l’arctangente ?
La dérivée de l’arctangente de x est un sur un plus x au carré.
![]()
Par conséquent, la dérivée de l’arctangente d’une fonction est égale au quotient de la dérivée de cette fonction divisé par un plus ladite fonction au carré.
![]()
Dans ce cas, la fonction a été représentée par un u, ce serait donc la formule de la dérivée de l’arctangente de la fonction u.
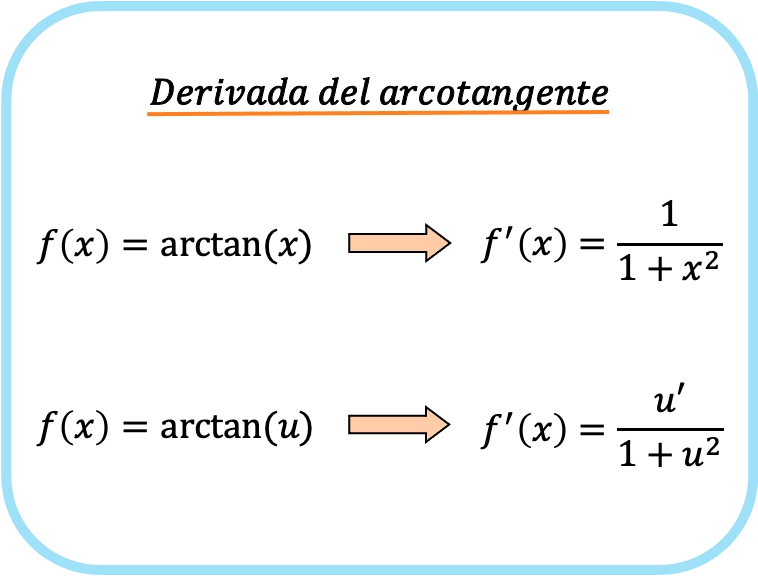
Comme vous pouvez le voir, la formule de la dérivée de la tangente inverse est très similaire aux formules des dérivées de l’arc sinus et de l’arc cosinus.
Exemples de dérivée de l’arctangente
Une fois que nous connaîtrons la formule de la dérivée de l’arctangente, nous allons expliquer la dérivation de plusieurs exemples de ce type de dérivées trigonométriques. De cette façon, il vous sera plus facile de comprendre comment est dérivée l’arctangente d’une fonction.
Exemple 1 : Dérivée de l’arctangente de 2x
![]()
On applique la formule pour résoudre la dérivée :
![]()
La dérivée de 2x est 2, donc la dérivée arctangente de 2x est 2 sur un plus 2x au carré :
![]()
Exemple 2 : Dérivée de l’arctangente de x au carré
![]()
Pour trouver le résultat de la dérivée de cet exemple, nous devons utiliser la formule de la dérivée de l’arctangente, qui est :
![]()
Ainsi, la dérivée de la fonction x 2 est 2x, donc la dérivée de l’arctangente de x élevée à la puissance 2 est :
![]()
Exemple 3 : Dérivée de l’arctangente du sinus de x
![]()
Logiquement, pour calculer la dérivée il faut appliquer la formule correspondante :
![]()
Dans ce cas nous avons une fonction composite, nous devons donc appliquer la règle de la chaîne pour calculer la dérivée de l’arctangente :
![]()
Exercices résolus sur la dérivée de l’arctangente
Dérivez les fonctions arctangentes suivantes :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
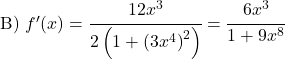
![]()
![]()
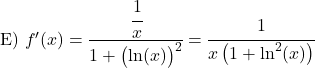
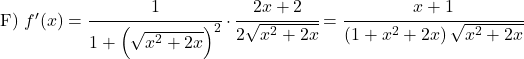
Démonstration de la formule de la dérivée de l’arctangente
Ensuite, nous allons prouver la formule de la dérivée de l’arctangente.
![]()
Nous convertissons d’abord l’arctangente en tangente en profitant du fait que l’arctangente est la fonction inverse de la tangente :
![]()
On différencie les deux côtés de l’équation :
![]()
Nous effaçons et’ :
![]()
D’autre part, grâce à l’identité trigonométrique fondamentale on sait que la somme des carrés du sinus et du cosinus est égale à 1. On peut donc transformer l’expression précédente en fraction :
![]()
![]()
On divise tous les termes par le carré du cosinus :
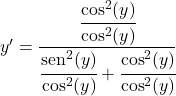
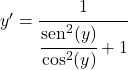
Le sinus divisé par le cosinus est égal à la tangente, donc :
![]()
![]()
Comme nous l’avons vu plus haut, la tangente est équivalente à la variable x, on peut donc substituer l’expression pour arriver à la formule de la dérivée de l’arctangente :
![]()