Dans cet article, nous expliquons comment dériver un quotient (ou une division) à partir de deux fonctions. Vous trouverez des exemples de dérivées de quotients de fonctions et, en plus, vous pourrez vous entraîner avec des exercices résolus pas à pas sur les dérivées de divisions.
Formule pour la dérivée d’un quotient
La derivada de un cociente (o una división) de dos funciones es igual al cociente de la derivada de la función del numerador por la función del denominador menos la función del numerador por la derivada de la función del denominador dividido por la función del denominador elevada carré.

Comme vous pouvez le voir, lorsqu’on applique la règle de dérivée d’un quotient (ou d’une division) on a encore une fraction après la différenciation. Mais, en plus, au numérateur nous avons deux multiplications et une soustraction, et le dénominateur est élevé à la puissance deux.
Exemples de dérivées de quotients
Nous venons de voir quelle est la formule de la dérivée d’un quotient de deux fonctions, nous résoudrons ensuite plusieurs exemples de dérivées de ce type d’opérations. N’oubliez pas que si vous ne comprenez pas comment est dérivé un quotient fonctionnel, vous pouvez nous le demander dans la section commentaires.
Exemple 1
Dans cet exemple, nous dériverons une fonction potentielle divisée par une fonction trigonométrique :
![]()
La formule de la dérivée d’une division de deux fonctions différentes est la suivante :
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Nous devons donc d’abord calculer la dérivée de chaque fonction séparément :
![]()
![]()
La dérivée de la fonction entière est donc :
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-65ce4673f3ad5a4c09a9b2e7c611821d_l3.png)
Exemple 2
Dans ce cas on trouvera la dérivée d’une constante divisée par une fonction :
![]()
Comme nous l’avons vu plus haut, la règle pour la dérivée d’une division de deux fonctions différentes est la suivante :
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Ainsi, nous calculons séparément la dérivée du numérateur et du dénominateur :
![]()
![]()
Et enfin, on trouve la dérivée de la division entière :
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f8bdea77dc91b1aff40695511593e86_l3.png)
En fait, nous pouvons dériver une formule pour différencier directement lorsque nous avons une constante au numérateur divisée par une fonction, car la dérivée de la constante est toujours 0. Par conséquent, la formule suivante sera toujours vraie :
![]()
Exemple 3
Dans cet exercice, nous dériverons un quotient de deux polynômes :
![]()
Pour résoudre la dérivée, il faut appliquer la règle de la dérivée d’un quotient de deux fonctions différentes, qui est la suivante :
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
Trouvons maintenant la dérivée du polynôme numérateur et du polynôme dénominateur :
![]()
![]()
La dérivée de la division des polynonymes est donc :
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-065ad49556f264b4cfb505522ad7566b_l3.png)
Et enfin, on fait les opérations et on simplifie la fraction au maximum :
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-af3f7cb513883d1fa5dadca23701c19d_l3.png)
Exercices résolus sur la dérivée d’un quotient
Dérivez les divisions de fonctions suivantes :
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-26b0af84dd46ca29727eee97380b4ca4_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11f9c8fda61edb1ce51bd33e022a0a24_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec87daa1a463bacd5a42a1b16e826449_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef2b22482e39cea7e82047c0d9911b0_l3.png)
Démonstration de la dérivée d’un quotient
Enfin, nous allons démontrer la formule de la dérivée d’une division. Pour ce faire, nous utiliserons la définition générale d’une dérivée, qui est :
![]()
Soit z une division de deux fonctions différentes :
![]()
Alors, la dérivée de la fonction z appliquant la définition mathématique sera :
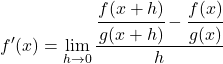
Nous résolvons la soustraction de fractions du numérateur de la fraction :
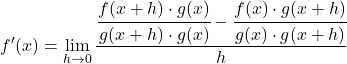
![]()
L’ajout d’un terme d’addition et de soustraction à une équation ne modifie pas l’équation. Nous pouvons donc passer à l’étape suivante :
![]()
On extrait le facteur commun :
![]()
Passons maintenant le terme h du dénominateur au numérateur en utilisant les propriétés des fractions :
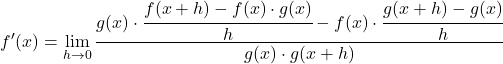
On transforme l’équation en appliquant les propriétés des limites :
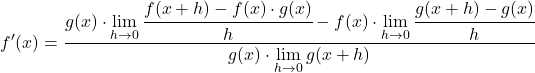
Les limites du numérateur correspondent précisément à la définition mathématique de la dérivée de chaque fonction, donc :
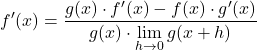
On résout la limite du dénominateur de la fraction :
![]()
Et ainsi est démontrée la formule de la dérivée d’un quotient de deux fonctions :
![]()