Vous découvrirez ici comment dériver la sécante d’une fonction. De plus, vous pourrez voir plusieurs exercices résolus étape par étape sur la dérivée de la sécante. Et enfin, vous trouverez la démonstration de la formule de ce type de dérivée trigonométrique.
Quelle est la dérivée de la sécante ?
La dérivée de la sécante de x est égale au produit de la sécante de x et de la tangente de x.
![]()
En appliquant des formules trigonométriques, la dérivée de la sécante de x peut également être définie comme le quotient du sinus de x divisé par le carré du cosinus de x.
![]()
Et si l’on applique la règle de la chaîne, la dérivée de la sécante d’une fonction est le produit de la sécante de la fonction par la tangente de la fonction par la dérivée de la fonction.
![]()
En résumé, la formule de la dérivée de la fonction sécante est la suivante :
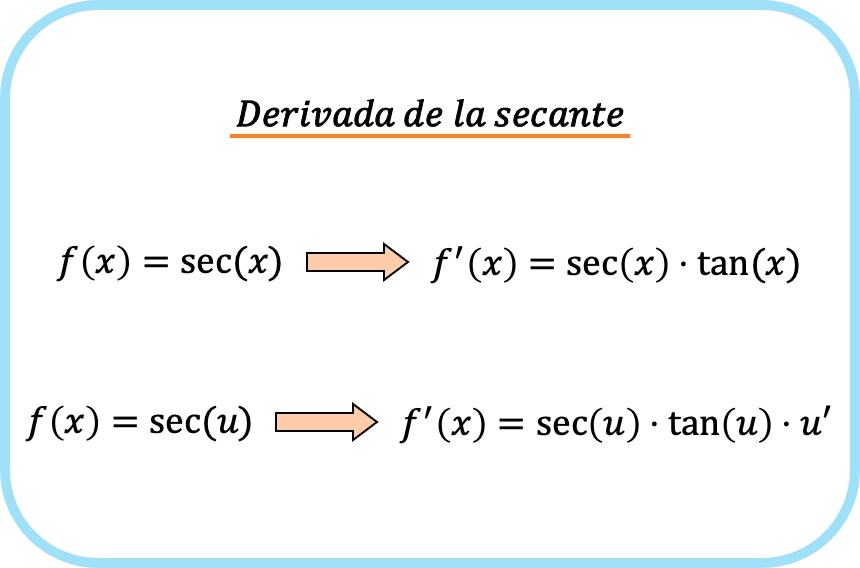
Exemples de dérivée de la sécante
Une fois que nous aurons vu quelle est la formule de la dérivée de la sécante, nous allons résoudre plusieurs exemples de ce type de dérivées trigonométriques.
Exemple 1 : Dérivée de la sécante de 2x
Dans cet exemple nous verrons à combien vaut la dérivée de la sécante de 2x :
![]()
Pour dériver la sécante de la fonction 2x, il faut utiliser sa formule correspondante. De plus, dans l’argument sécant, nous avons une fonction autre que x, nous devons donc appliquer la règle de la chaîne.
![]()
La fonction 2x est linéaire, donc sa dérivée est 2. Par conséquent, pour trouver la dérivée, il faut simplement remplacer le u par 2x et le u’ par 2 dans la formule :
![]()
Exemple 2 : Dérivée de la sécante de x au carré
Dans cet exercice nous verrons quelle est la dérivée de la sécante de x au carré :
![]()
Pour dériver la sécante d’une fonction, vous pouvez utiliser l’une des deux formules vues ci-dessus, mais dans ce cas, nous différencierons la fonction avec la formule de multiplication entre la sécante et la tangente.
![]()
La dérivée de x élevée à la puissance 2 donne 2x, donc la dérivée de la sécante de x au carré est :
![]()
Exemple 3 : Dérivée du cube sécant d’un polynôme
![]()
La règle pour la dérivée de la sécante d’une fonction est :
![]()
Mais dans ce cas, nous devons dériver une fonction composée, puisque la sécante est élevée à la puissance trois et, de plus, dans son argument nous avons une fonction polynomiale. Donc, pour différencier la fonction entière, nous devons appliquer la règle de la chaîne :
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
Exercices résolus sur la dérivée d’une sécante
Dérivez les fonctions sécantes suivantes :
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
Démonstration de la formule de la dérivée de la sécante
Ensuite, nous prouverons la formule de la dérivée de la sécante. Même s’il n’est évidemment pas nécessaire de connaître la preuve par cœur, il est toujours bon de comprendre d’où viennent les formules.
Mathématiquement, la définition de la sécante est l’inverse multiplicatif du cosinus :
![]()
Par conséquent, nous pouvons essayer de dériver la sécante en utilisant la règle du quotient :
![]()
Et, comme nous l’avons vu dans la première section, l’expression précédente peut être convertie en formule de la dérivée de la sécante. Pour ce faire, on sépare la fraction en deux fractions différentes :
![]()
La division du sinus par le cosinus équivaut à la tangente, on remplace donc ledit quotient par la tangente :
![]()
Selon la définition mathématique de la fonction sécante, le cosinus est son inverse multiplicatif. Ainsi en remplaçant un divisé par le cosinus par la sécante on arrive à la formule de sa dérivée :
![]()