Asymptote horizontale

Dans cet article, nous expliquons ce que sont les asymptotes horizontales d’une fonction et comment elles sont calculées. De plus, vous trouverez plusieurs exemples de ce type d’asymptotes pour bien comprendre le concept et, en plus, vous pourrez vous entraîner avec des exercices résolus d’asymptotes horizontales.

Qu’est-ce qu’une asymptote horizontale ?

Une asymptote horizontale d’une fonction est une droite horizontale dont son graphe se rapproche indéfiniment sans jamais la croiser. Par conséquent, l’équation d’une asymptote horizontale est y=k , où k est la valeur de l’asymptote horizontale.

Autrement dit, k est une asymptote horizontale si la limite de la fonction lorsque x tend vers l’infini est égale à k .

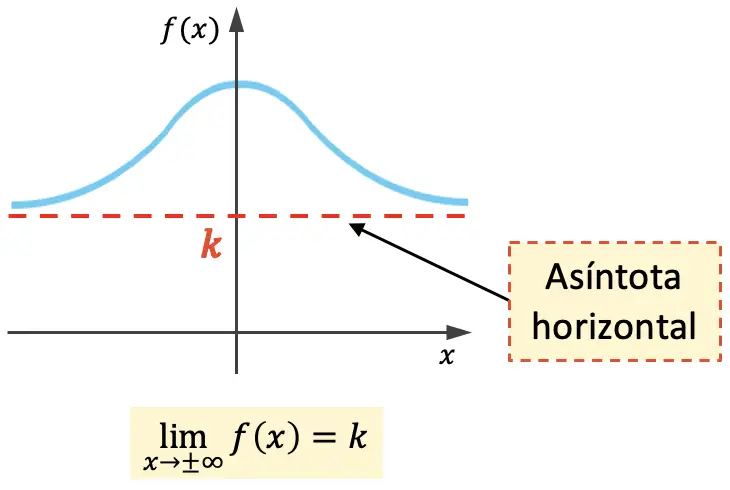
asymptote horizontale d'une fonction

La fonction ci-dessus a une asymptote horizontale des deux côtés du graphe, mais une fonction ne peut avoir une asymptote horizontale que d’un côté :

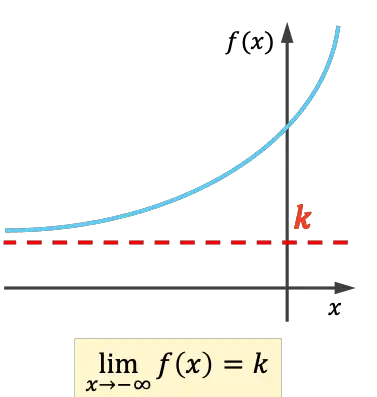
  • La fonction a une asymptote horizontale à gauche si la limite au moins à l’infini donne un nombre réel.
  • La fonction a une asymptote horizontale vers la droite si la limite à plus l’infini donne un nombre réel.
asymptote horizontale d'une fonction à partir de la gauche
asymptote horizontale à droite

Comment calculer l’asymptote horizontale d’une fonction

Pour calculer l’asymptote horizontale d’une fonction, les étapes suivantes doivent être suivies :

  1. Calculer la limite de la fonction aux infinis (+∞ et -∞).
  2. Si une limite à l’infini donne un nombre réel (k), la droite y=k est une asymptote horizontale de la fonction.
  3. Si aucune des deux limites ne correspond à un nombre réel, la fonction n’a pas d’asymptotes horizontales.

Exemple d’asymptote horizontale

Pour que vous puissiez voir un exemple de la façon dont cela est fait, nous allons retirer toutes les asymptotes horizontales de la fonction rationnelle suivante :

f(x)=\cfrac{x+1}{x-1}

Pour déterminer les asymptotes horizontales, il faut calculer la limite à l’infini moins et à l’infini plus de la fonction :

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Voir : comment résoudre l’indétermination infini entre infini

Les deux bornes à l’infini donnent 1, donc y=1 est la seule asymptote horizontale de la fonction.

Ci-dessous la fonction représentée graphiquement. Comme vous pouvez le voir, la fonction devient très proche de y=1 (à la fois à plus l’infini et à moins l’infini), mais elle ne le touche jamais car c’est une asymptote horizontale.

exemple d'asymptote horizontale

Remarque : dans certains cas particuliers, la fonction coupe l’asymptote horizontale en un ou plusieurs points, mais en général le graphe d’une fonction ne croise jamais ses asymptotes.

D’autre part, cette fonction a aussi une asymptote verticale en x=1. Parce que, comme vous pouvez le voir sur le graphique, il se rapproche beaucoup de la ligne x=1 mais il n’atteint jamais cette valeur.

Problèmes résolus d’asymptotes horizontales

Exercice 1

Trouvez l’asymptote horizontale, le cas échéant, de la fonction fractionnaire suivante :

\displaystyle f(x)= \frac{4x+3}{2x-1}

Pour déterminer les asymptotes horizontales de la fonction rationnelle, il faut calculer les bornes à l’infini de la fonction :

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

Dans ce cas, le résultat de la forme indéterminée ∞/∞ est la division des coefficients des x de degré le plus élevé, puisque le numérateur et le dénominateur sont du même ordre.

Les limites à plus l’infini et moins l’infini de la fonction donnent 2, donc y=2 est une asymptote horizontale et est la seule que possède la fonction.

Exercice 2

Trouvez toutes les asymptotes horizontales de la fonction rationnelle suivante avec une racine :

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Pour trouver les asymptotes horizontales de la fonction, nous calculons d’abord la limite à l’infini positif :

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

Et puis on résout la limite de la fonction à moins l’infini :

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Si vous avez des doutes sur la façon dont les limites à l’infini ont été résolues, nous vous recommandons de consulter le lien ci-dessus sur la façon de résoudre l’indétermination infinie entre l’infini.

Dans ce cas, nous avons obtenu deux valeurs différentes des bornes à l’infini. La fonction a donc deux asymptotes horizontales : y=3 est une asymptote horizontale de la fonction à droite et, d’autre part, y=-3 est une asymptote horizontale de la fonction à gauche.

Exercice 3

Calculez les asymptotes horizontales de la fonction définie par morceaux suivante :

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Pour calculer les asymptotes horizontales de la fonction, il n’y a pas de formule, mais il faut calculer les limites à plus et moins l’infini.

Ainsi, pour trouver la limite au moins infinie, on prend la fonction définie dans la première section :

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Ainsi la droite y=0 est une asymptote horizontale à gauche de la fonction.

Et maintenant, nous calculons la limite à plus l’infini en prenant la fonction définie dans la deuxième section :

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

Ainsi la droite y=1/2 est une asymptote horizontale à droite de la fonction.

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top