Dérivée d'une fonction linéaire

Dans cet article, nous vous montrons combien est la dérivée d’une fonction linéaire. De plus, nous résolvons plusieurs exemples de dérivées de fonctions linéaires et nous démontrons la formule de ce type de dérivée. Vous trouverez même des exercices résolus sur les dérivées de fonctions linéaires.

Quelle est la dérivée d’une fonction linéaire ?

La dérivée d’une fonction linéaire est le coefficient du terme du premier degré , c’est-à-dire que la dérivée d’une fonction linéaire f(x)=Ax+B est égale à A .

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

Le terme indépendant est supprimé de la dérivée car la dérivée d’une constante est égale à zéro. Et, d’autre part, la dérivée d’un terme du premier degré est le coefficient dudit terme. Par conséquent, la dérivée de la somme de ces deux types de fonctions est le coefficient du terme linéaire.

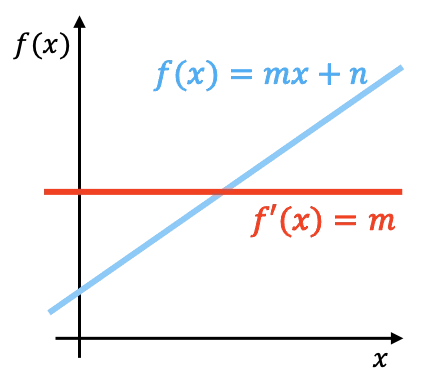
Géométriquement, la dérivée d’une fonction linéaire est la pente de cette fonction. Dans le graphique ci-dessus, vous pouvez voir représenté une fonction linéaire avec sa dérivée.

Exemples de dérivées de fonctions linéaires

Etant donné la définition de la dérivée d’une fonction linéaire, nous allons calculer plusieurs exemples de fonctions linéaires pour finir de comprendre le concept :

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Gardez à l’esprit que la dérivée de la fonction linéaire est toujours le nombre qui accompagne la variable x lorsque la fonction n’a pas de terme indépendant, ou en d’autres termes, si elle n’a qu’un terme du premier degré. Par exemple:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Par conséquent, la dérivée d’une fonction linéaire est une fonction sans variable indépendante, un nombre simple.

Preuve de la dérivée d’une fonction linéaire

Ensuite, nous allons démontrer la formule de la dérivée d’une fonction linéaire.

Soit f une fonction linéaire quelconque :

$f(x)=Ax+B$

La formule pour calculer la dérivée d’une fonction en un point est :

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Donc, si nous calculons la limite précédente pour une fonction linéaire, nous obtenons :

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

On résout les parenthèses :

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

On opère au numérateur :

$\displaystyle f'(a)=\frac{Ah}{h}$

Et enfin, on simplifie la fraction :

$\displaystyle f'(a)=A$

En conclusion, la dérivée d’une fonction linéaire est égale au coefficient du terme du premier degré en tout point. Ainsi, la formule de la dérivée d’une fonction linéaire est prouvée.

Problèmes résolus de dérivées de fonctions linéaires

Calculez les dérivées des fonctions linéaires suivantes :

$\text{A)}\ f(x)=2x-25$

$\text{B)}\ f(x)=x+3$

$\text{C)}\ f(x)=-9x-1$

$\text{D)}\ f(x)=\cfrac{1}{2}x+7$

$\text{E)}\ f(x)=5x$

$\text{F)}\ f(x)=\sqrt{7}x+\frac{3}{4}$

voir solution

Pour dériver une fonction linéaire, il suffit d’éliminer le terme constant et la variable de la fonction, de sorte qu’il ne reste que le coefficient du terme linéaire. Pourtant:

$\text{A)}\ f'(x)=2$