Dérivée de la cosécante

Dans cet article, nous expliquons comment dériver la cosécante d’une fonction (formule). Vous trouverez également des exercices résolus pas à pas de la dérivée de la cosécante. Et enfin, vous pourrez voir la démonstration de la formule de ce type de dérivée trigonométrique.

Formule dérivée cosécante

La dérivée de la cosécante de x est égale à moins le quotient du cosinus de x divisé par le sinus carré de x.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

En utilisant les formules trigonométriques, on peut également définir la dérivée de la cosécante de x comme moins le produit de la cotangente de x fois la cosécante de x.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

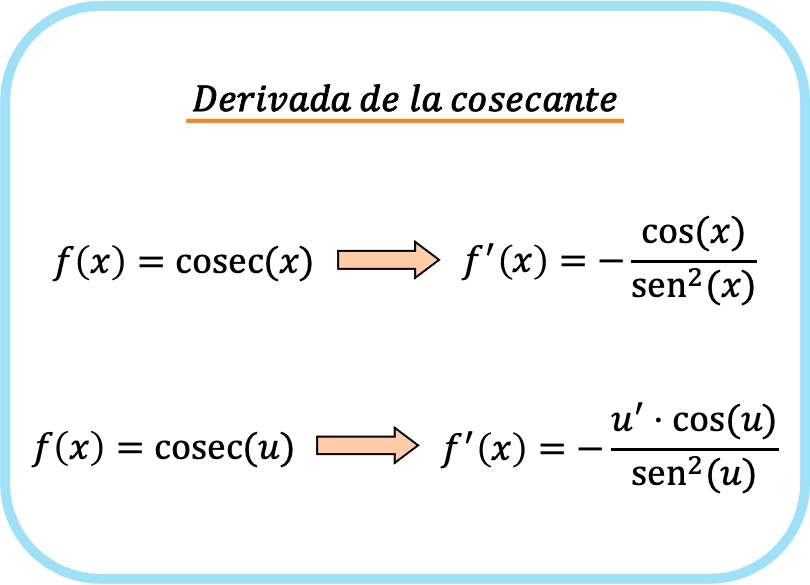
Et si nous appliquons la règle de la chaîne, la dérivée de la cosécante d’une fonction est moins le produit de la dérivée de la fonction par le cosinus de la fonction, divisé par le sinus carré de la fonction.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

La formule utilisée pour dériver la cosécante d’une fonction est donc la suivante :

Exemples de dérivée de la cosécante

Après avoir vu ce qu’est la formule de la dérivée de la cosécante, nous allons maintenant donner plusieurs exemples. Ainsi, vous pouvez voir exactement comment la cosécante d’une fonction est dérivée.

Exemple 1 : Dérivée de la cosécante de 2x

Dans cet exemple nous allons voir combien vaut la dérivée de la cosécante de 2x :

$f(x)=\text{cosec}(2x)$

La fonction d’argument cosécante est différente de x, nous devons donc utiliser la règle de dérivée cosécante avec la règle de chaîne.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Donc, pour trouver la dérivée de cette fonction trigonométrique, il suffit de substituer les valeurs dans la formule précédente : dans l’argument cosinus et sinus on met 2x, et u’ correspond à la dérivée de 2x, soit 2 :

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

Exemple 2 : Dérivée de la cosécante de x au carré

Dans cet exercice, nous verrons combien vaut la dérivée de la cosécante de x au carré :

$f(x)=\text{cosec}(x^2)$

Logiquement, la dérivée de cette fonction trigonométrique est résolue à l’aide de la formule de la dérivée de la cosécante :

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

La dérivée de x au carré donne 2x, donc la dérivée de la cosécante de x à la puissance deux est :

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

Exemple 3 : Dérivée de la cosécante au cube d’une fonction exponentielle

$f(x)=\text{cosec}^3(e^{5x})$

Quel que soit l’argument de la fonction, la règle de la dérivée de la cosécante d’une fonction est :

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Mais dans ce cas, nous avons une fonction composée, car la cosécante est élevée à trois et, de plus, dans son argument, il y a une fonction exponentielle. Donc, pour faire la dérivation de toute la fonction, nous devons appliquer la règle de la chaîne plusieurs fois :

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

Problèmes résolus de la dérivée de la cosécante

Dérivez les fonctions cosécantes suivantes :

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

voir solution

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

Preuve de la formule de la dérivée de la cosécante

Ensuite, nous allons démontrer la formule de la dérivée de la cosécante. Contrairement à d’autres démonstrations, dans ce cas nous n’utiliserons pas la limite qui définit une dérivée, mais nous partirons de la définition mathématique de la cosécante.

Algébriquement, la fonction trigonométrique cosécante est l’inverse multiplicatif du sinus :

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

On peut donc prendre la dérivée de la cosécante en utilisant la règle du quotient :

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

Comme vous pouvez le voir, ce n’est qu’en appliquant la règle de la dérivée d’une division que nous arrivons à la formule de la dérivée de la cosécante. Et puisque la dérivée d’un quotient est déjà prouvée (vous pouvez le voir dans le lien suivant), la règle de la dérivée cosécante est également prouvée.

➤ Voir : preuve de la dérivée d’un quotient

Formule dérivée cosécante

Exemples de dérivée de la cosécante

Exemple 1 : Dérivée de la cosécante de 2x

Exemple 2 : Dérivée de la cosécante de x au carré

Exemple 3 : Dérivée de la cosécante au cube d’une fonction exponentielle

Problèmes résolus de la dérivée de la cosécante

Preuve de la formule de la dérivée de la cosécante

Leave a Comment Cancel Reply