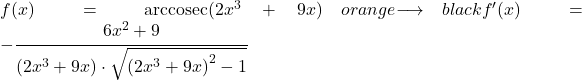Sur cette page, vous verrez quelle est la formule de la dérivée de l’arccosécante. De plus, vous pourrez voir des exercices résolus de dérivées de l’arc cosécante d’une fonction.
Formule dérivée arccosécante
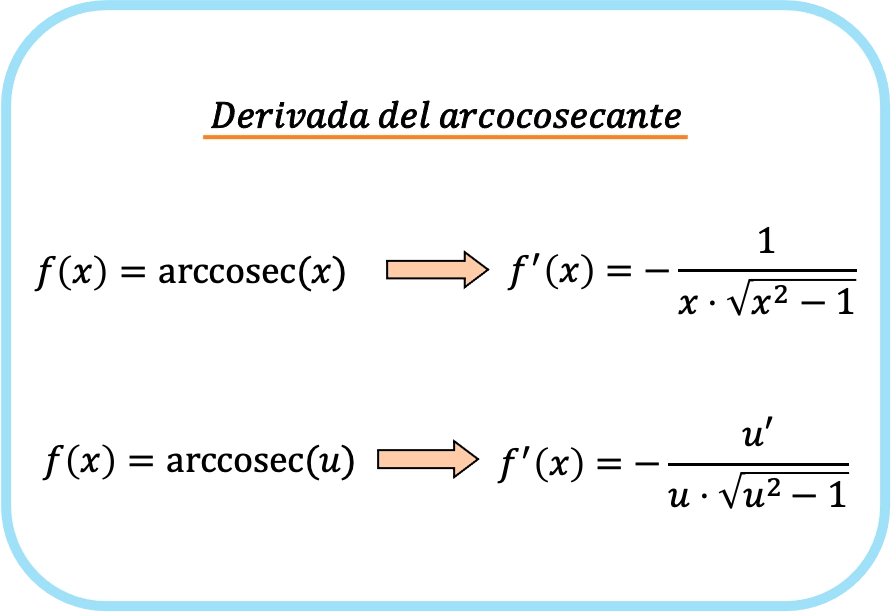
La dérivée de l’arccosécante de x est moins un sur le produit de x fois la racine de x au carré moins 1.
![]()
Par conséquent, la dérivée de l’arccosécante d’une fonction est égale à moins le quotient de la dérivée de cette fonction divisé par la fonction multipliée par la racine de cette fonction au carré moins un.
![]()
En fait, les deux formules précédentes sont les mêmes, mais dans la deuxième expression, la règle de la chaîne est appliquée. En fait, si vous substituez la fonction identité x dans le u, vous obtiendrez la dérivée de l’arccosécante de x puisque la dérivée de x est un.
Comme vous le savez bien, l’arccosécante est la fonction trigonométrique inverse de la cosécante, cependant, ses dérivées sont assez différentes. Vous pouvez voir la formule de cet autre type de fonction trigonométrique dans le lien suivant :
➤ Voir : dérivée de la cosécante
Exemples de dérivée de l’arc cosécant
En voyant ce qu’est la règle de la dérivée arccosécante, nous allons ensuite résoudre deux exemples de ce type de dérivée. Mais si vous avez encore des questions sur la façon de dériver l’arc cosécant, vous pouvez nous les poser dans les commentaires.
Exemple 1
Dans cet exemple, nous verrons de combien est la dérivée de l’arc cosécante de la fonction quadratique x 2 .
![]()
Pour calculer la dérivée de l’arccosécante de x au carré, on applique la formule que l’on a vue plus haut :
![]()
La dérivée de x à la puissance deux est 2x, donc la dérivée de la fonction composée est :
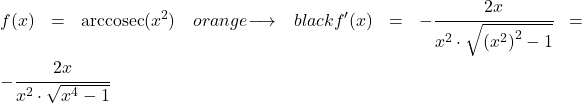
Exemple 2
Dans ce deuxième exemple, nous dériverons l’arccosécante d’une fonction potentielle.
![]()
Nous devons utiliser la règle de la dérivée arcsecante pour trouver la dérivée de la fonction entière.
![]()
Ainsi, au numérateur, nous écrivons la dérivée de l’argument de la fonction, et au dénominateur, nous réécrivons la fonction potentielle et la multiplions par la racine carrée de la fonction de l’argument élevée au carré moins 1 :