Sur cette page nous allons voir comment additionner et soustraire des matrices . Vous avez également des exemples qui vous aideront à le comprendre parfaitement et des exercices résolus pour que vous puissiez vous entraîner. Vous trouverez également toutes les propriétés de l’addition matricielle.
Comment faire une addition et une soustraction de matrices ?
Pour calculer une addition (ou soustraction) de deux matrices, il faut additionner (ou soustraire) les éléments qui occupent la même position dans les matrices.
Exemples:

Notez que pour additionner ou soustraire deux matrices, elles doivent avoir la même dimension. Par exemple, les matrices suivantes ne peuvent pas être additionnées car la première est une matrice 2×2 et la seconde est une matrice 3×2 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-082c648e15685c4ddeac2cc2da502d96_l3.png)
Exercices résolus d’addition et de soustraction de matrices
Exercice 1
Calculez la somme suivante de matrices 2×2 :
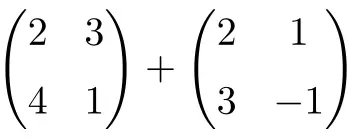
C’est une somme de deux matrices carrées de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d9428ad89a6bd149d5e63bc500879ac_l3.png)
Exercice 2
Effectuez la soustraction matricielle suivante :
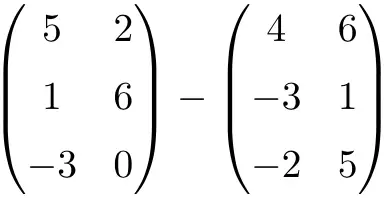
C’est une soustraction de deux matrices de dimension 3×2 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c371e1f01df59f4b8abb018e476e66d7_l3.png)
Exercice 3
Trouvez le résultat de la somme matricielle suivante de dimension 3×3 :
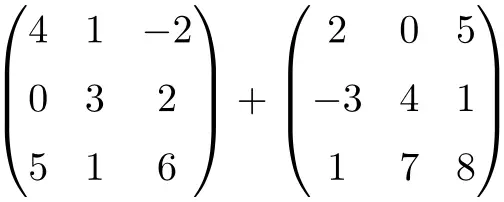
C’est une somme de deux matrices carrées d’ordre 3×3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-280299cb0b37e1a585466c4570439ec4_l3.png)
Exercice 4
Calculez l’addition et la soustraction suivantes de matrices carrées d’ordre 2 :
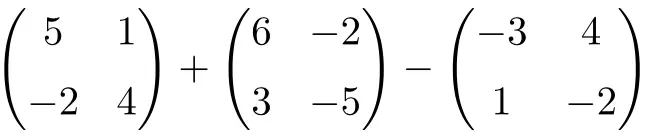
C’est une opération combinée avec une addition et une soustraction de matrices carrées d’ordre 2 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9fa4dba7699c0035ce5081756b4f62e_l3.png)
Donc, d’abord, nous ajoutons les matrices à gauche :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e1544e4da9d5ad2ea3ec2e4ad0326023_l3.png)
Et puis on calcule la soustraction de matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd7f32fc7c9429fdfc3b5b745e85975c_l3.png)
Exercice 5
Résolvez l’addition et la soustraction matricielle suivantes :
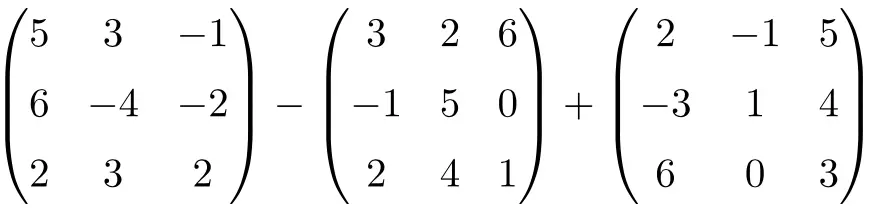
C’est une opération combinée d’une soustraction et d’une addition de matrices carrées d’ordre 3 :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae66268adcd61258654056815542cf58_l3.png)
Premièrement, nous résolvons la soustraction de matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4401b28babce2beaaa6f840c4ed8c959_l3.png)
Et enfin on fait l’addition des matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffba1ade3d98c434960b54fc0c7ffe1f_l3.png)
Maintenant que vous savez additionner et soustraire des matrices, c’est le bon moment pour voir comment multiplier des matrices , sûrement la plus importante des opérations matricielles. Vous trouverez également des exercices résolus pas à pas de multiplication matricielle afin que vous puissiez vous entraîner, comme dans toutes les pages de ce site. 😉
Propriétés d’ajout de matrice
L’addition matricielle répond aux caractéristiques suivantes :
- L’addition matricielle a la propriété commutative :
![]()
Par conséquent, l’ordre dans lequel nous ajoutons les matrices est le même. Pour le démontrer, nous ajouterons deux matrices en changeant leur ordre et vous verrez comment le résultat est le même.
Nous procédons donc à l’addition de deux matrices dans un certain ordre :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7eb454436dc3268ae8d6d2b62f395a7_l3.png)
A noter que si on inverse l’ordre d’addition des matrices, le résultat reste le même :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c1e9cd77bc490913ed30ff63815da355_l3.png)
- Une autre propriété de l’addition matricielle est celle de l’ élément opposé :
![]()
Autrement dit, si nous ajoutons une matrice plus la même matrice mais avec tous ses éléments changés de signe, le résultat sera une matrice nulle :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-add832e83fe554143cbd4c710315c1c0_l3.png)
- L’addition matricielle a également la propriété d’élément neutre :
![]()
Cette propriété est la plus évidente, elle fait référence au fait que toute matrice plus une matrice pleine de zéros est équivalente à la même matrice :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac7b0ba246075c196188798be2c6a034_l3.png)
- L’addition matricielle a la propriété associative :
![]()
Par conséquent, l’ordre dans lequel nous ajoutons les matrices est le même. Regardez l’exemple suivant, où nous ajoutons 3 matrices avec un ordre différent et le résultat est le même :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bae8e10bca43351f3a84f83bfe50ab55_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cc2b7a14cacc7e403cd729cd863d309_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab1f88e74b139451eccb0471988c3db_l3.png)