Sur cette page nous allons voir comment faire des puissances de matrices. Vous trouverez également des exemples et des exercices résolus pas à pas de puissances de matrices qui vous aideront à le comprendre parfaitement. Vous apprendrez également quelle est la nième puissance d’une matrice et comment la trouver.
Comment est calculée la puissance d’une matrice ?
Pour calculer la puissance d’une matrice , il faut multiplier la matrice par elle-même autant de fois que le dit l’exposant. Par exemple:
![]()
Par conséquent, pour obtenir la puissance d’une matrice, vous devez savoir comment résoudre la multiplication matricielle . Sinon, vous ne pouvez pas calculer une matrice de puissance.
Exemple de calcul de la puissance d’une matrice :

Par conséquent, la puissance d’une matrice au carré est calculée en multipliant la matrice par elle-même. De même, une matrice au cube est égale à la matrice au carré de la matrice elle-même. De même, pour trouver la puissance d’une matrice élevée à quatre, la matrice élevée à trois doit être multipliée par la matrice elle-même. Et ainsi de suite.
Il y a une propriété importante de la puissance matricielle que vous devez connaître : la puissance d’une matrice ne peut être calculée que lorsqu’elle est carrée , c’est-à-dire lorsqu’elle a le même nombre de lignes que de colonnes.
Quelle est la puissance n d’une matrice ?
La nième puissance d’une matrice est une expression qui nous permet de calculer facilement n’importe quelle puissance d’une matrice.
Souvent, les puissances des matrices suivent un modèle . Par conséquent, si nous parvenons à déchiffrer la séquence qu’ils suivent, nous pourrons calculer n’importe quelle puissance sans avoir à faire toutes les multiplications.
Cela signifie que nous pouvons trouver une formule qui nous donne la nième puissance d’une matrice sans avoir à calculer toutes les puissances.
Astuces pour découvrir le schéma suivi par les puissances :
- La parité de l’exposant . Il se peut que les puissances paires soient dans un sens et les puissances impaires dans l’autre.
- Variation des signes. Par exemple, il se pourrait que les éléments des puissances paires soient positifs et les éléments des puissances impaires soient négatifs, ou vice versa.
- Répétition : si la même matrice est répétée tous les certain nombres de puissances ou non.
- Il faut aussi regarder s’il existe une relation entre l’exposant et les éléments de la matrice.
Exemple de calcul de la puissance n d’une matrice :
- Être
 la matrice suivante, calculez
la matrice suivante, calculez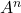 et
et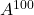 .
.
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60016ce1c6799c93007526681fbf4894_l3.png)
Nous allons d’abord calculer plusieurs puissances de la matrice
![]() , pour essayer de deviner le modèle suivi par les puissances. Alors on calcule
, pour essayer de deviner le modèle suivi par les puissances. Alors on calcule![]() ,
,![]() ,
,![]() et
et ![]()
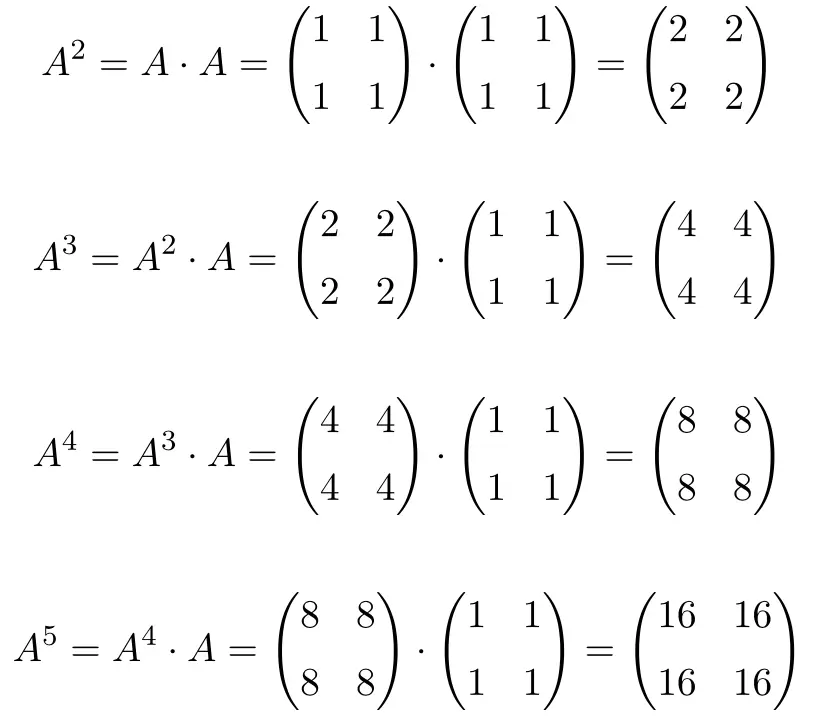
Lors du calcul jusqu’à
![]() , on voit que les puissances de la matrice
, on voit que les puissances de la matrice![]() Elles suivent un schéma : pour chaque augmentation de puissance, le résultat est multiplié par 2. Par conséquent, toutes les matrices sont des puissances de 2 :
Elles suivent un schéma : pour chaque augmentation de puissance, le résultat est multiplié par 2. Par conséquent, toutes les matrices sont des puissances de 2 :
![Rendered by QuickLaTeX.com \displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ec7ee835cf9eda6a4f9d497e8baff79_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-69c6ff0f4de92192584dadc4719167c7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f724a50b220b3026d53e40ee17870359_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f08f7cc00465a6a098ce7d752aa66f_l3.png)
Nous pouvons donc dériver la formule de la nième puissance de la matrice
![]()
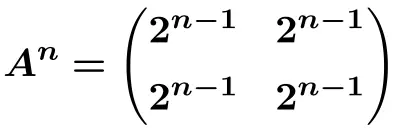
Et à partir de cette formule, nous pouvons calculer
![]()
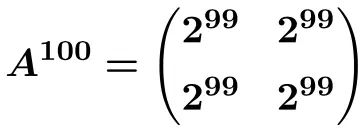
Problèmes résolus de puissances de matrices
Exercice 1
Soit la matrice suivante de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdf81cf9fb956a144c7bda96a84ec7db_l3.png)
Calculer:
![]()
Pour calculer la puissance d’une matrice, il faut multiplier la matrice une par une. Par conséquent, nous calculons d’abord
![]()
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24916b0b0e4431b0a2ee2b09875dc903_l3.png)
Maintenant on calcule
![]()
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57f79bd420c0044c84a64b431035b8ea_l3.png)
Et enfin on calcule
![]()
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbc2ad8229ee141b323c9bbcc9df00fd_l3.png)
Exercice 2
Soit la matrice d’ordre 2 suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33db03560b5c28f45eef9aa293484603_l3.png)
Calculer:
![]()
![]() est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Alors calculons
est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Alors calculons![]() pour essayer de comprendre la séquence qu’ils suivent:
pour essayer de comprendre la séquence qu’ils suivent:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb9646cc984d754d2a618e6223e93cd3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22fdee28399b9115de98a214ba0c8473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1a085a2338ce1e74885ca04bbd0011a7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc357146829da8323a0755fa16a8ca8_l3.png)
De cette façon, nous pouvons voir le modèle que suivent les puissances : à chaque puissance, tous les nombres restent les mêmes, sauf l’élément de la deuxième colonne de la deuxième ligne, qui est multiplié par 3. Par conséquent, tous les nombres restent toujours les mêmes. et le dernier élément est une puissance de 3 :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a0bfa34768808832e0fd5d3f730eb27b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6e007f5ad5d38fd887d39f00bd2b9fc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-585d8a00f418b50f60b4f95d87c5839c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dec6b9db4b59d9759adf85cee442cca3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7244b46950df4d9107cbdb7ad004e17_l3.png)
Donc la formule de la nième puissance de la matrice
![]() est:
est:
![Rendered by QuickLaTeX.com \displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-beec2f1ed3e47902de0f25fe1901e294_l3.png)
Et à partir de cette formule, nous pouvons calculer
![]()
![Rendered by QuickLaTeX.com \displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa3261646ca7bfa41f8ad46331a0af4b_l3.png)
Exercice 3
Soit la matrice 3×3 suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f11fe8a7dcd1e308faa0af24eee3f362_l3.png)
Calculer:
![]()
![]() est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Alors calculons
est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Alors calculons![]() pour essayer de comprendre la séquence qu’ils suivent:
pour essayer de comprendre la séquence qu’ils suivent:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acb15d7f461d11e3668bc0b96a1fdc06_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f416625ded948830fa80799249c12608_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a76fd60051b157f06c2a731ff575d1e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3409c7b8d82ffd21cc084a12405fce74_l3.png)
De cette façon, nous pouvons voir le modèle que suivent les puissances : à chaque puissance, tous les nombres restent les mêmes, sauf les fractions, qui augmentent d’une unité au numérateur :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-86c72aa2b21e7a68bbebfe7af5daa420_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce805455e49bf018f8f22588391ac44c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd5468ece9001274493687f3786b0af3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07fd0e03c0163b58fffbe0235009fd8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ea88723757d1f2d8d6de1ac2d3843c7_l3.png)
Donc la formule de la puissance de la nième matrice
![]() est:
est:
![Rendered by QuickLaTeX.com \displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56308ff348d67ba1aba5816d85e9ee1c_l3.png)
Et à partir de cette formule, nous pouvons calculer
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5352f021f5ab30e999c57f978ff55ad6_l3.png)
Exercice 4
Soit la matrice suivante de taille 2×2 :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4609248b534d656aa9495b58f42e343f_l3.png)
Calculer:
![]()
![]() est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Dans ce cas, il faut calculer
est une puissance trop grande pour être calculée à la main, de sorte que les puissances de la matrice doivent suivre un modèle. Dans ce cas, il faut calculer![]() afin de connaître la séquence qu’ils suivent:
afin de connaître la séquence qu’ils suivent:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9a1fb4cf8bb75cf02d76a26054e6bfa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-110c4b30c78811cafdd4234e128ed414_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2b1976bbdf3c1daa9d75497efc07975c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0266d832a2fc0a04c9f6582dc231d57_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21dea9844b7bfdb990bbb2bc955c866e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-788e75a71c1dfe4a60f0e52960715efe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4947286a163847383e3735a508b0037d_l3.png)
Avec ces calculs, nous pouvons voir que toutes les 4 puissances, nous obtenons la matrice d’identité. C’est-à-dire qu’il nous donnera comme résultat la matrice identité des puissances
![]() ,
,![]() ,
,![]() ,
,![]() ,… Donc pour calculer
,… Donc pour calculer![]() il faut décomposer 201 en multiples de 4 :
il faut décomposer 201 en multiples de 4 :
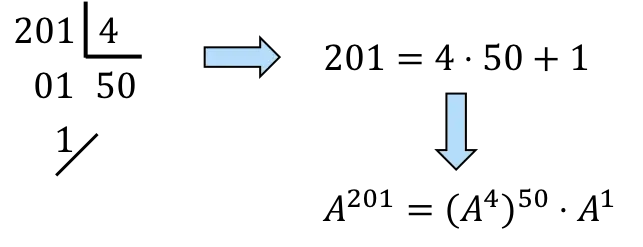
![]() , pourtant,
, pourtant,![]() ce sera 50 fois
ce sera 50 fois![]() et une fois
et une fois ![]()
![]()
Et comment savons-nous que
![]() est la matrice identité
est la matrice identité ![]()
![]()
![]()
De plus, la matrice identité élevée à un nombre quelconque donne la matrice identité. Pourtant:
![]()
Et enfin, toute matrice multipliée par la matrice d’identité donne la même matrice. Donc:
![]()
Pour ce que
![]() est égal à
est égal à ![]()
![Rendered by QuickLaTeX.com \displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1214abe876a5aede8fbbce79009d5dbc_l3.png)
Exercice 5
Soit la matrice d’ordre 3 suivante :
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f3ba8b2d15b622f99774be05aa2620_l3.png)
Calculer:
![]()
Évidemment, calculez la puissance de la matrice
![]() C’est un calcul trop important pour être fait à la main, donc les puissances de la matrice doivent suivre un modèle. Dans ce cas, il faut calculer
C’est un calcul trop important pour être fait à la main, donc les puissances de la matrice doivent suivre un modèle. Dans ce cas, il faut calculer![]() afin de connaître la séquence qu’ils suivent:
afin de connaître la séquence qu’ils suivent:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4032b55d68a5615911a5b7c997b05e6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b5deef2a7728c5e82e1a1dafb1a939c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62e856d037138b2ead39b17ccebf96d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854da5c09b6662da46acb790afb6d01a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9f804a1c129e18d105fb92254c971fa_l3.png)
Avec ces calculs, nous pouvons voir que toutes les 3 puissances, nous obtenons la matrice d’identité. C’est-à-dire qu’il nous donnera comme résultat la matrice identité des puissances
![]() ,
,![]() ,
,![]() ,
,![]() ,… Si bien que pour calculer
,… Si bien que pour calculer![]() Il faut décomposer 62 en multiples de 3 :
Il faut décomposer 62 en multiples de 3 :
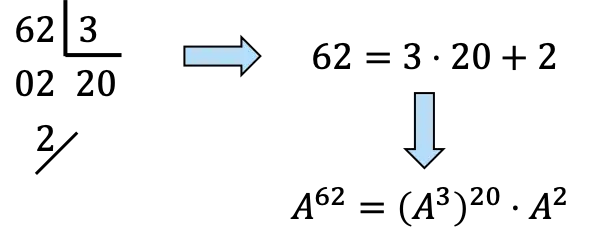
![]() , pourtant,
, pourtant,![]() ce sera 20 fois
ce sera 20 fois![]() et une fois
et une fois ![]()
![]()
Et comment savons-nous que
![]() est la matrice identité
est la matrice identité ![]()
![]()
![]()
De plus, la matrice identité élevée à un nombre quelconque donne la matrice identité. Pourtant:
![]()
Enfin, toute matrice multipliée par la matrice d’identité donne la même matrice. Pourtant:
![]()
Pour ce que
![]() sera égal à
sera égal à![]() , dont nous avons calculé le résultat précédemment :
, dont nous avons calculé le résultat précédemment :
![Rendered by QuickLaTeX.com \displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f95e17aacde501ca1c28dbf14324f0b_l3.png)
Si ces exercices sur les puissances des matrices carrées vous ont été utiles, vous pouvez également trouver des exercices résolus pas à pas sur l’addition et la soustraction de matrices , l’une des opérations les plus utilisées avec les matrices.