Sur cette page, vous verrez ce qu’est la règle de Cramer et, en plus, vous trouverez des exemples et des exercices avec la résolution de systèmes d’équations par la règle de Cramer.
Qu’est-ce que la règle de Cramer ?
La règle de Cramer est une méthode utilisée pour résoudre des systèmes d’équations par des déterminants. Voyons comment il est utilisé :
Soit un système d’équations :
![Rendered by QuickLaTeX.com \begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0141f3451719f665ef28e4061489551_l3.png)
La matrice A et la matrice étendue A’ du système sont :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d628a13ec7de4b3ba7a301c0a5d8ac6_l3.png)
La règle de Cramer dit que la solution d’un système d’équations est :
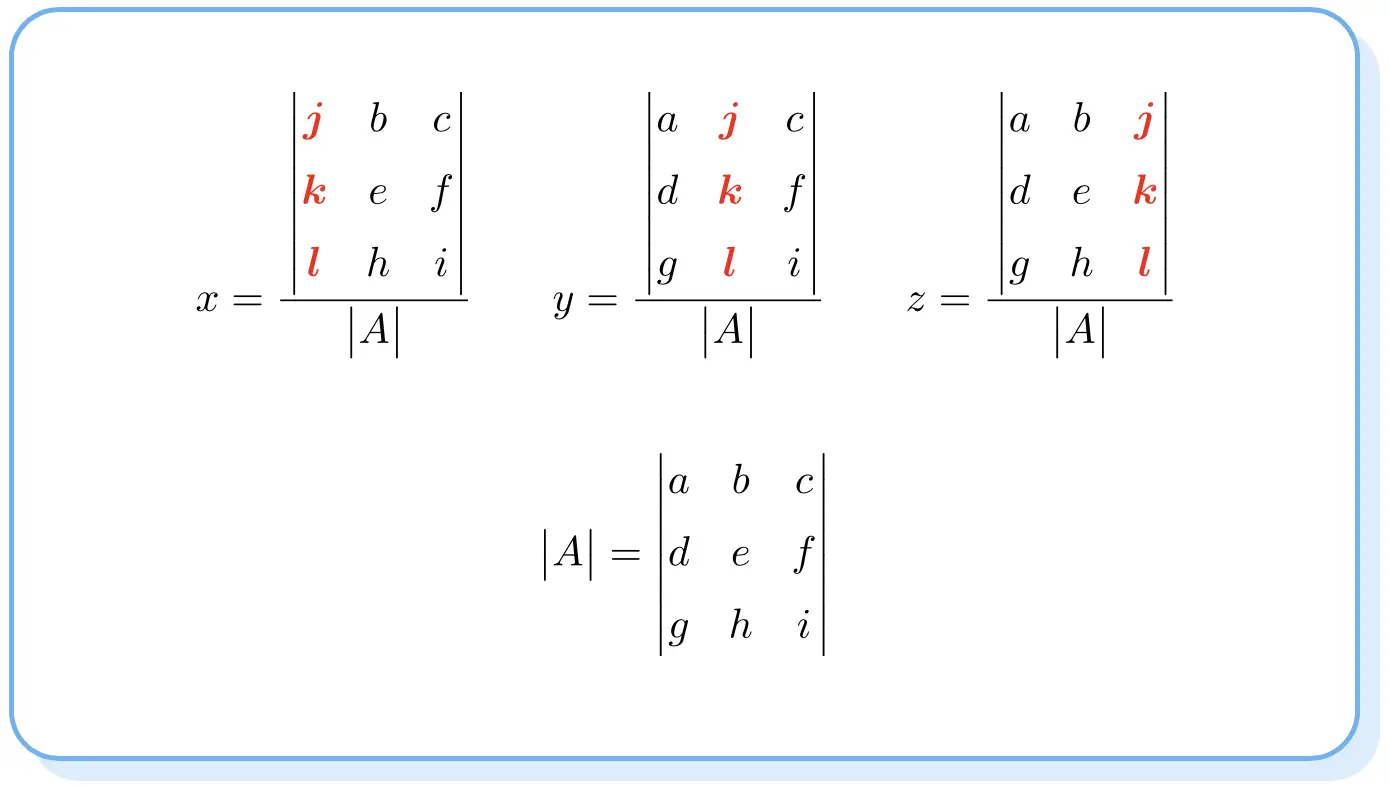
Notez que les déterminants des numérateurs sont comme le déterminant de la matrice A mais en changeant la colonne de chaque inconnue pour la colonne des termes indépendants.
Par conséquent, la règle de Cramer est utilisée pour résoudre des systèmes d’équations linéaires. Mais, comme vous le savez déjà, il existe de nombreuses façons de résoudre un système d’équations, par exemple la méthode de Gauss Jordan est bien connue.
Vous trouverez ci-dessous des exemples de résolution de systèmes d’équations linéaires avec la règle de Cramer, ou parfois également écrite comme la règle de Kramer.
Exemple 1 : système compatible déterminé (SCD)
- Résolvez le système suivant de 3 équations à 3 inconnues en utilisant la règle de Cramer :
![Rendered by QuickLaTeX.com \begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6013b7e73c89c24fe388f1a5d018f32b_l3.png)
On fait tout d’abord la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c710ed86223f47f39b5a25720b5ca19d_l3.png)
Nous calculons maintenant le rang des deux matrices, dans le but de voir de quel type de système il s’agit. Pour calculer le rang de A, on calcule le déterminant 3×3 de toute la matrice (en utilisant la règle de Sarrus) et on regarde si ça donne 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae4a3bb88d113494463df8e670c326c6_l3.png)
Le déterminant de A est différent de 0, donc la matrice A est de rang 3.
![]()
Donc la matrice A’ est aussi de rang 3 , puisqu’elle ne peut pas être de rang 4 et doit être au moins du même rang que la matrice A.
![]()
L’étendue de la matrice A est égale à l’étendue de la matrice A’ et au nombre d’inconnues du système (3), donc, par le théorème de Rouché-Frobenius , nous savons qu’il s’agit d’un système compatible déterminé (SCD) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Une fois que nous savons que le système est un SCD, nous appliquons la règle de Cramer pour le résoudre. Pour ce faire, rappelons que la matrice A, son déterminant et la matrice A’ sont :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b2b3e5865c2264c360fb887d37a5f6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a604d8f5a3927a47a264d28f7a007b2_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1fa494ffb5e452d59c4d2dad40f925a_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08e3dabe2f33434eb96658491f67c0b4_l3.png)
Calculer
![]() Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96e76cb8867224755e9c19254678abd4_l3.png)
La solution du système d’équations est donc :
![]()
Exemple 2 : Système compatible indéterminé (SCI)
- Résolvez le système d’équations suivant à l’aide de la règle de Cramer :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-781530aac4d8507fd6c7cbd77c3b4651_l3.png)
On fait tout d’abord la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a64800a78bf8e2e2f547be907e6863cb_l3.png)
Maintenant, nous calculons la plage des deux matrices et pouvons ainsi voir de quel type de système il s’agit. Pour calculer le rang de A, nous calculons le déterminant de la matrice entière (en utilisant la règle de Sarrus) et vérifions s’il vaut 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-581c58cbe0fdd9952e7e25b919ecc33b_l3.png)
Le déterminant donne 0, donc la matrice A n’est pas de rang 3. Mais elle a un déterminant 2×2 différent de 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Donc la matrice A est de rang 2 :
![]()
Une fois que l’on connaît l’étendue de la matrice A, on calcule celle de la matrice A’. Le déterminant des 3 premières colonnes donne 0, donc on essaie les autres déterminants 3×3 possibles dans la matrice A’ :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-686e7ca635ecee685005f6013c2e64ad_l3.png)
Tous les déterminants d’ordre 3 donnent 0. Mais, évidemment, la matrice A’ a le même déterminant non-0 2×2 que la matrice A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Donc, la matrice A’ est aussi de rang 2 :
![]()
Donc, puisque le rang de la matrice A est égal au rang de la matrice A’ mais que ces deux sont plus petits que le nombre d’inconnues du système (3), on sait par le théorème de Rouché-Frobenius qu’il s’agit d’un Compatible Indéterminé Système (ICS) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Lorsque nous voulons résoudre un système indéterminé compatible (SCI), nous devons transformer le système : nous éliminons d’abord une équation, puis nous convertissons une variable en λ (généralement la variable z), et enfin nous mettons les termes avec λ ensemble avec le termes indépendants.
Une fois que nous avons transformé le système, nous appliquons la règle de Cramer et nous obtiendrons la solution du système en fonction de λ.
Dans ce cas, nous éliminerons la dernière équation du système :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0511fecc9c2af695b6b8eccae6b0661_l3.png)
Convertissons maintenant la variable z en λ :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d6142d2be611954fd849a032a97245a_l3.png)
Et on met les termes avec λ avec les termes indépendants :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00214205f2334f1c9bc10810c1c1df83_l3.png)
Donc, la matrice A et la matrice A’ du système restent :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c4b47303973b823a1c5628f5448ca79_l3.png)
Enfin, une fois que nous avons transformé le système, nous appliquons la règle de Cramer . On résout donc le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b79f52dc82f5cfc311867273e78c06_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ff917eaea976c65bd18e0476078d3cb_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-155ca520739bbf7e040a6cdc632f7c27_l3.png)
Alors que la solution du système d’équations est une fonction de λ, puisque c’est un SCI et, par conséquent, il a une infinité de solutions :
![]()
Problèmes résolus de la règle de Cramer
Exercice 1
Appliquez la règle de Cramer pour résoudre le système suivant de deux équations à 2 inconnues :
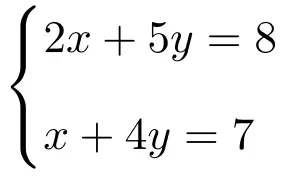
La première chose à faire est la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a001db9cf56846150730fee7126dacd_l3.png)
Il faut maintenant trouver le rang de la matrice A. Pour cela, on vérifie si le déterminant de toute la matrice est différent de 0 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c75c1c344c286016bea83237f1f418e_l3.png)
Comme la matrice a un déterminant 2×2 différent de 0, la matrice A est de rang 2 :
![]()
Une fois que nous connaissons le rang de A, nous calculons le rang de A’. Celui-ci sera au moins de rang 2, car nous venons de voir qu’il a à l’intérieur un déterminant d’ordre 2 différent de 0. De plus, il ne peut pas être de rang 3, puisqu’on ne peut pas faire de déterminant 3×3. Donc, la matrice A’ est aussi de rang 2 :
![]()
Par conséquent, en appliquant le théorème de Rouché-Frobenius, nous savons qu’il s’agit d’un système compatible déterminé (SCD), car la plage de A est égale à la plage de A’ et au nombre d’inconnues.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbd67b16bb6d52a0696e70a77833cd3b_l3.png)
Une fois que nous savons que le système est un SCD, nous appliquons la règle de Cramer pour le résoudre.
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0adeda8f2ce557661466996038b1148_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-59790a66cc31fac07be1d5a7bb556d9e_l3.png)
La solution du système d’équations est donc :
![]()
Exercice 2
Trouver la solution du système suivant de trois équations à 3 inconnues par la règle de Cramer :
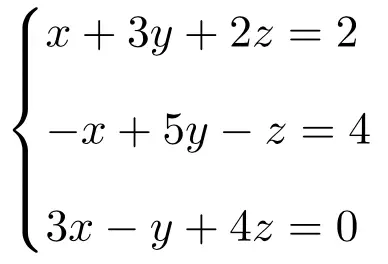
On fait tout d’abord la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-eea75fbf6d86ebc3d0b9e236cd2160f5_l3.png)
On trouve maintenant le rang de la matrice A en calculant le déterminant de la matrice 3×3 avec la règle de Sarrus :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73f751f3b5c527c16b5de1b10bf07a4e_l3.png)
La matrice ayant un déterminant d’ordre 3 différent de 0, la matrice A est de rang 3 :
![]()
Par conséquent, la matrice A’ est également de rang 3 :
![]()
Par conséquent, en utilisant le théorème de Rouché-Frobenius, nous savons qu’il s’agit d’un système compatible déterminé (SCD), car la plage de A est égale à la plage de A’ et au nombre d’inconnues.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Une fois que nous savons que le système est un SCD, nous devons appliquer la règle de Cramer pour résoudre le système.
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc574297f609b68e4fb48466ec6c8077_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2544601137d62e217ff1866f278203d6_l3.png)
Calculer
![]() Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42d7d4adcfc48954185ca14b56b8e128_l3.png)
La solution du système d’équations est donc :
![]()
Exercice 3
Calculer la solution du système suivant de trois équations à 3 inconnues par la règle de Cramer :
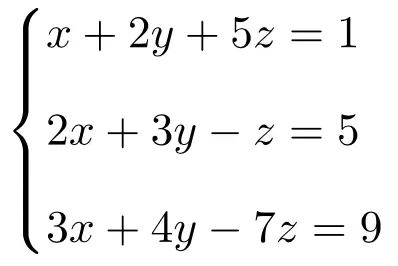
On fait d’abord la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-afd359275e5ebaaf3229504c47a5815f_l3.png)
On calcule l’étendue de la matrice A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ddf17a2b3eed5a680d685900a79b31_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdd4380c7c76418bd3ec12c94359f886_l3.png)
![]()
Une fois que l’on connaît l’étendue de la matrice A, on calcule celle de la matrice A’. Le déterminant des 3 premières colonnes donne 0, donc on essaie les autres déterminants 3×3 possibles dans la matrice A’ :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-1addc62130e0462075b3bade26a7e35e_l3.png)
Tous les déterminants d’ordre 3 donnent 0. Cependant, la matrice A’ a le même déterminant 2×2 non-0 que la matrice A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7de377466bd5afd03f58f9b532324e75_l3.png)
Donc, la matrice A’ est aussi de rang 2 :
![]()
Puisque le rang de la matrice A est égal au rang de la matrice A’ mais que ces deux sont inférieurs au nombre d’inconnues du système (3), on sait par le théorème de Rouché-Frobenius qu’il s’agit d’un Système Compatible Indéterminé ( SCI) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Étant un système SCI, nous devons éliminer une équation. Dans ce cas, nous éliminerons la dernière équation du système :
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a1d067e155540f4345cf56e5c1567d3_l3.png)
Convertissons maintenant la variable z en λ :
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5fa91777a722d3783b2f887aab44152_l3.png)
Et on met les termes avec λ avec les termes indépendants :
![Rendered by QuickLaTeX.com \begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76ff21181be050b01c247981298986a7_l3.png)
De telle sorte que la matrice A et la matrice A’ du système restent :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-230e5b28dd467127e63f4f9756cf90da_l3.png)
Enfin, une fois que nous avons transformé le système, nous appliquons la règle de Cramer . On résout donc le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1](https://mathority.org/wp-content/ql-cache/quicklatex.com-f127efbd217e2bca8852ec792610732f_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42652a14362b42e606841b6bb3e77cc0_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b95c5870f1762a2d82c9ebcccbca7408_l3.png)
Alors que la solution du système d’équations est une fonction de λ, puisque c’est un SCI et, par conséquent, il a une infinité de solutions :
![]()
Exercice 4
Résoudre le problème suivant d’un système de trois équations à 3 inconnues en appliquant la règle de Cramer :
![Rendered by QuickLaTeX.com \begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e1c3458f33b863db10750b9e51d09e_l3.png)
D’abord, on construit la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-743a40010cb4a610e8a3fc6ae5d313b4_l3.png)
Calculons maintenant le rang de la matrice A en calculant le déterminant de la matrice 3×3 en utilisant la règle de Sarrus :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-713c634fbc3e1b1cb228e3891c9bff1c_l3.png)
La matrice ayant un déterminant d’ordre 3 différent de 0, la matrice A est de rang 3 :
![]()
Par conséquent, la matrice A’ est également de rang 3, puisqu’elle doit être au moins du même rang que la matrice A et elle ne peut pas être de rang 4 car c’est une matrice de dimension 3×4.
![]()
Par conséquent, en utilisant le théorème de Rouché-Frobenius, nous en déduisons qu’il s’agit d’un système compatible déterminé (SCD), car la plage de A est égale à la plage de A’ et au nombre d’inconnues.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Une fois que nous savons que le système est un SCD, nous devons appliquer la règle de Cramer pour résoudre le système.
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a290479c69ff806f19dcf29f96e1228_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bba0765fbcbcebf0585520af25b4a30_l3.png)
Calculer
![]() Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la troisième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bc157a8c4dfe8ee4651affac68ef878_l3.png)
La solution du système d’équations linéaires est donc :
![]()
Exercice 5
Résolvez le système d’équations linéaires suivant à l’aide de la règle de Cramer :
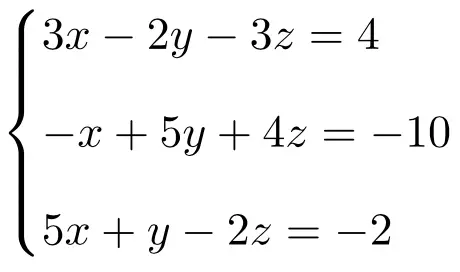
On fait tout d’abord la matrice A et la matrice étendue A’ du système :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5153b5951b768cc3cafa2bb2567ba92_l3.png)
On calcule l’étendue de la matrice A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3778c9499e2a44ea3834dfed1523163_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03d70742b14ced92f33963df0c86e92f_l3.png)
![]()
Une fois que l’on connaît l’étendue de la matrice A, on calcule celle de la matrice A’. Le déterminant des 3 premières colonnes donne 0, donc on essaie les autres déterminants 3×3 possibles dans la matrice A’ :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bed93d532ae4ccd4649a73662f55f0f_l3.png)
Tous les déterminants d’ordre 3 donnent 0. Mais, évidemment, la matrice A’ a le même déterminant d’ordre 2 autre que 0 que la matrice A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-858d95d7d252b16706b66c0e6aba09c4_l3.png)
Donc, la matrice A’ est aussi de rang 2 :
![]()
Le rang de la matrice A est égal au rang de la matrice A’ mais ces deux sont plus petits que le nombre d’inconnues du système (3), donc par le théorème de Rouché-Frobenius on sait que c’est un Système Indéterminé Compatible ( SCI ):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Étant un système SCI, nous devons éliminer une équation. Dans ce cas, nous éliminerons la dernière équation du système :
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e10bd826663dff41c4272610cbc07b1_l3.png)
Convertissons maintenant la variable z en λ :
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2502be450040b38761c08e5d6beaf379_l3.png)
Et on met les termes avec λ avec les termes indépendants :
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80a43d98e6be30965d554e8a89aa5d89_l3.png)
De telle sorte que la matrice A et la matrice A’ du système restent :
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3451ce571163983cf41794d4998283d6_l3.png)
Enfin, une fois que nous avons transformé le système, nous appliquons la règle de Cramer . On résout donc le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7a7d6208ea5e762f5c74a44e6838cf_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la première colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c30fcc0526c2d4112eb4f60a3d8847f_l3.png)
Pour calculer l’inconnu
![]() Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
Avec la règle de Cramer, on change la deuxième colonne du déterminant de A par la colonne des termes indépendants et on la divise par le déterminant de A :
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdb22a54274e019c811c9051502c474a_l3.png)
Ainsi, la solution du système d’équations est une fonction de λ, puisqu’il s’agit d’un SCI et, par conséquent, le système a une infinité de solutions :
![]()