Combinaison linéaire de vecteurs -

Sur cette page, vous trouverez l’explication de ce que signifie une combinaison linéaire entre vecteurs. De plus, vous pourrez voir un exemple de la façon dont un vecteur est exprimé sous forme de combinaison linéaire et, en plus, vous pourrez vous entraîner avec des exercices et des problèmes résolus étape par étape.

Qu’est-ce que la combinaison linéaire de vecteurs ?

La définition de la combinaison linéaire est la suivante :

Une combinaison linéaire d’un ensemble de vecteurs est le vecteur obtenu en additionnant tous les vecteurs de l’ensemble multipliés par des scalaires (nombres réels).

Autrement dit, étant donné un ensemble de vecteurs

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$ une combinaison linéaire d’entre eux serait :

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

Où les coefficients

$a_i$ Ce sont des chiffres réels.

Par conséquent, un vecteur qui est une combinaison linéaire d’autres vecteurs signifie que le premier peut être exprimé en fonction du second.

Ce concept peut être mieux compris en représentant graphiquement un vecteur dans le plan qui est une combinaison linéaire de deux vecteurs :

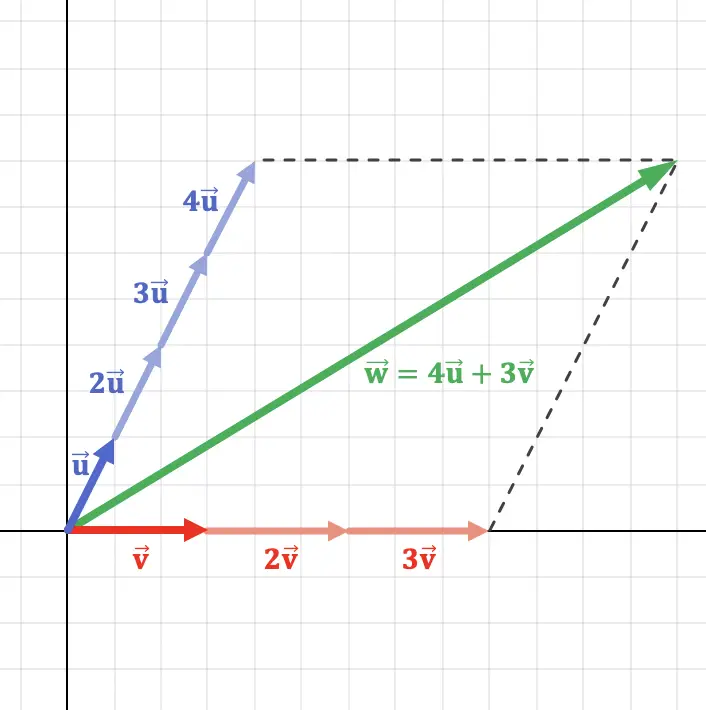
combinaison linéaire de vecteurs dans r3

Comme vous pouvez le voir dans la représentation graphique ci-dessus, le vecteur

$\vv{\text{w}}$ peut être obtenu à partir des vecteurs $\vv{\text{u}}$ et $\vv{\text{v}}$ faire des opérations vectorielles. Par conséquent, le vecteur $\vv{\text{w}}$ est une combinaison linéaire des deux autres vecteurs.

Il faut souligner que cette combinaison linéaire est unique , ou en d’autres termes, il n’existe qu’une seule combinaison linéaire réalisable pour chaque vecteur. Puisque, suivant l’exemple précédent, si l’on multipliait

$\vv{\text{u}}$ pour 6 au lieu de 4, on obtiendrait un autre vecteur différent.

De plus, une des propriétés de la combinaison linéaire dans le plan (dans R2) est que tout vecteur peut être mis comme une combinaison linéaire de deux autres vecteurs s’ils ont des directions différentes, c’est-à-dire s’ils ne sont pas parallèles.

En outre, on peut parfois identifier à l’œil nu que deux vecteurs sont une combinaison linéaire. Pour ce faire, il suffit que ses composantes soient proportionnelles . Par exemple, les coordonnées des deux vecteurs suivants sont proportionnelles et, par conséquent, les vecteurs sont une combinaison linéaire :

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Enfin, que ce soit dans un espace vectoriel bidimensionnel (dans R2) ou tridimensionnel (dans R3), s’il existe une combinaison linéaire au sein d’un ensemble de vecteurs, cela implique qu’ils sont linéairement dépendants les uns des autres. En revanche, si aucune combinaison linéaire n’est possible entre les vecteurs, cela signifie qu’ils sont linéairement indépendants .

Si ce dernier concept ne vous est pas tout à fait clair, nous vous recommandons de consulter notre explication sur les vecteurs linéairement dépendants et indépendants , vous trouverez ici ce que signifie pour les vecteurs d’être linéairement dépendants ou indépendants, des exemples de chaque type et les différences entre eux. . Ce concept est beaucoup utilisé et, en fait, il est souvent posé lors des examens, il est donc important que vous le compreniez bien.

Comment exprimer un vecteur comme une combinaison linéaire d’autres vecteurs

Nous allons ensuite voir comment résoudre un problème typique dans lequel on nous demande de trouver la combinaison linéaire d’un vecteur.

Exprimer le vecteur 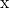$\vv{\text{x}}$ comme une combinaison linéaire de 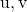$\vv{\text{u}}, \vv{\text{v}}$ et $\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

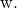
Pour que le vecteur

$\vv{\text{x}}$ être une combinaison linéaire des autres vecteurs, l’équation suivante doit être remplie :

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

Où les coefficients

$a_1, a_2$ et $a_3$ Ce sont les inconnues que nous devons trouver.

On remplace donc chaque vecteur par ses coordonnées :

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

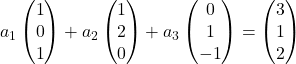
On multiplie chaque vecteur par son coefficient :

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

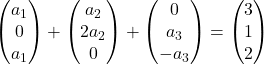
On fait l’addition de vecteurs :

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

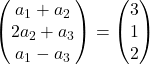
Chaque coordonnée de gauche doit être égale à chaque coordonnée de droite. Nous avons donc 3 équations :

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

Il ne reste donc plus qu’à résoudre le système d’équations obtenu. Pour cela, utilisez la méthode que vous préférez (méthode de substitution, règle de Cramer, méthode de Gauss-Jordan,…), dans ce cas nous utiliserons la méthode de Gauss :

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

Le système d’étapes obtenu est donc :

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

Il ne nous reste plus qu’à clarifier les inconnues et trouver sa valeur. Donc à partir de la dernière équation on trouve

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

A partir de la deuxième équation du système, nous calculons la valeur de

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

Et enfin, à partir de la première équation du système d’étapes, nous trouvons l’inconnue

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

La solution du système d’équations linéaires est donc :

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

Donc le vecteur

$\vv{\text{x}}$ Il peut être exprimé par la combinaison linéaire suivante :

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

Il existe donc effectivement une dépendance linéaire entre les vecteurs. En revanche, si l’on n’avait obtenu aucune solution au système d’équations, cela signifierait que le vecteur

$\vv{\text{x}}$ Il est linéairement indépendant par rapport aux autres vecteurs et, par conséquent, il n’y aurait pas de combinaison linéaire possible pour obtenir ledit vecteur à partir des autres vecteurs.

Exercices résolus sur la combinaison linéaire de vecteurs

Exercice 1

Parmi les trois vecteurs suivants, indiquez quelles paires sont des combinaisons linéaires les unes des autres. De plus, trouvez la relation de combinaison linéaire desdites paires de vecteurs.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

Voir la solution

Pour savoir si une paire de vecteurs est une combinaison linéaire, il faut voir si leurs coordonnées sont proportionnelles.

Nous vérifions d’abord le vecteur

$\vv{\text{u}}$ avec le vecteur $\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

Deuxièmement, nous vérifions le vecteur

$\vv{\text{u}}$ avec le vecteur $\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

Enfin, nous testons le vecteur

$\vv{\text{v}}$ avec le vecteur $\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

Ainsi, la seule paire de vecteurs qui sont des combinaisons linéaires est

$\vv{\text{v}}$ et $\vv{\text{w}}.$ De plus, leur relation est la suivante :

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

Ou équivalent:

$\vv{\text{w}}= -3 \vv{\text{v}}$

Bien que l’énoncé ne le demande pas, les seuls vecteurs qui dépendent linéairement les uns des autres sont

$\vv{\text{v}}$ et $\vv{\text{w}}$ car il existe une combinaison linéaire entre eux. Les autres couples sont linéairement indépendants, car ils ne peuvent pas être combinés linéairement.

Exercice 2

Trouver la relation linéaire entre le vecteur

$\vv{\text{x}}$ et l’ensemble des vecteurs $\vv{\text{u}}, \vv{\text{v}}$ et $\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

Voir la solution

Pour que le vecteur

$\vv{\text{x}}$ être une combinaison linéaire des autres vecteurs, l’équation suivante doit être remplie :

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

On remplace donc chaque vecteur par ses coordonnées :

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

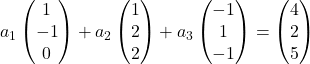
On multiplie chaque vecteur par sa constante :

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

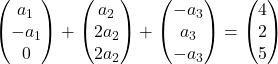
On ajoute les vecteurs :

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

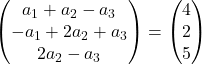
On obtient donc le système d’équations suivant :

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

On résout le système obtenu par la méthode de Gauss :

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

Le système d’étapes obtenu est donc :

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

Il ne nous reste plus qu’à clarifier les inconnues et trouver sa valeur. Donc à partir de la dernière équation on trouve

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

A partir de la deuxième équation du système, nous calculons la valeur de

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

Et enfin, à partir de la première équation du système d’étapes, nous trouvons l’inconnue

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

La solution du système d’équations linéaires est donc :

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

Donc le vecteur

$\vv{\text{x}}$ Il peut être exprimé par la combinaison linéaire suivante :

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

Exercice 3

Exprimer le vecteur

$\vv{\text{x}}$ comme une combinaison linéaire de vecteurs $\vv{\text{u}}, \vv{\text{v}}$ et $\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

Voir la solution

Nous proposons l’équation de combinaison linéaire par rapport au vecteur

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

On remplace donc chaque vecteur par ses composantes :

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

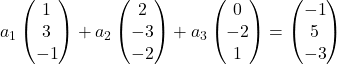
On multiplie chaque vecteur par son inconnue respective :

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

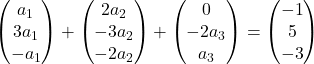
On effectue l’addition de vecteurs :

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

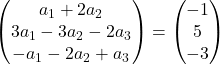
Nous avons donc obtenu le système d’équations suivant :

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

On résout le système obtenu par la méthode de Gauss :

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

Le système d’étapes obtenu est donc :

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

Il ne nous reste plus qu’à clarifier les inconnues et trouver sa valeur. Donc à partir de la dernière équation on trouve

$a_3:$

$a_3 = -4$

A partir de la deuxième équation du système, nous trouvons la valeur de

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

Et enfin, à partir de la première équation du système d’étapes, nous résolvons l’inconnue

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

La solution du système d’équations linéaires est donc :

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

Donc le vecteur

$\vv{\text{x}}$ peut être exprimé en combinant linéairement les autres vecteurs :

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

Exercice 4

Déterminer si le vecteur

$\vv{\text{x}}$ peut être exprimé sous la forme d’une combinaison linéaire à partir des vecteurs $\vv{\text{u}}, \vv{\text{v}}$ et $\vv{\text{w}}.$ Dans ce cas, trouvez l’expression qui les relie.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

Voir la solution

Pour que le vecteur

$\vv{\text{x}}$ être une combinaison linéaire des autres vecteurs, l’équation suivante doit être remplie :

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

On remplace donc chaque vecteur par ses coordonnées :

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

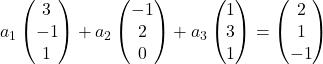
On multiplie chaque vecteur par son coefficient :

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

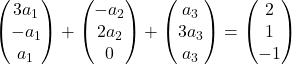
On ajoute les vecteurs :

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

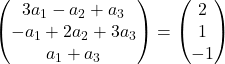
L’expression précédente est donc équivalente au système d’équations suivant :

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

Nous résolvons maintenant le système obtenu par la méthode de Gauss :

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

Nous avons donc obtenu le système d’équations suivant :

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

Cependant, la dernière équation ne pourra jamais être remplie, puisque 0 ne sera jamais égal à -30 quelles que soient les valeurs que prennent les inconnues. Par conséquent, le système n’a pas de solution et cela implique qu’il n’existe pas de combinaison linéaire permettant de calculer le vecteur

$\vv{\text{x}}.$

Qu’est-ce que la combinaison linéaire de vecteurs ?

Comment exprimer un vecteur comme une combinaison linéaire d’autres vecteurs

Exercices résolus sur la combinaison linéaire de vecteurs

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply