Sur cette page vous trouverez l’explication de la règle (ou loi) du parallélogramme. De plus, vous pourrez voir plusieurs exemples d’addition et de soustraction de vecteurs utilisant la règle du parallélogramme, ainsi que des applications réelles.
Quelle est la règle du parallélogramme ?
Comme vous le savez déjà, les quantités vectorielles ne peuvent pas être additionnées ou soustraites de la même manière que les nombres réels, car elles ont 2 composantes (en R2) ou 3 composantes (en R3) et parce que les vecteurs peuvent avoir des directions différentes. Par conséquent, d’autres méthodes sont nécessaires pour effectuer des opérations vectorielles, telles que la règle du parallélogramme, qui consiste en ce qui suit :
En mathématiques, la règle du parallélogramme est une procédure qui permet d’ajouter ou de soustraire deux vecteurs à leur représentation graphique.
La méthode du parallélogramme est sûrement la plus utilisée dans l’addition et la soustraction de vecteurs (graphiquement), car c’est une technique très facile à utiliser. Par exemple, en physique, il est utilisé pour additionner et soustraire des forces.
D’autre part, la règle varie légèrement selon que nous voulons ajouter ou soustraire des vecteurs, nous expliquerons donc ci-dessous les deux versions séparément.
Règle de parallélogramme pour ajouter deux vecteurs
Si nous voulons ajouter graphiquement deux vecteurs, les étapes pour appliquer la règle ou la loi du parallélogramme sont :
- Premièrement, nous dessinons les vecteurs et les positionnons au même point d’application, c’est-à-dire que nous plaçons les origines des deux vecteurs au même point.
- Ensuite, nous traçons à la fin d’un vecteur une ligne parallèle à l’autre vecteur. Et nous répétons l’étape avec l’autre vecteur. On obtiendra donc le dessin d’un parallélogramme (d’où le nom de la règle).
- Enfin, le vecteur résultant de la somme sera la diagonale du parallélogramme qui va de l’origine commune des vecteurs au point d’intersection des deux droites parallèles.
Dans l’exemple générique suivant, vous pouvez voir comment la règle du parallélogramme est utilisée :

Si vous souhaitez vous entraîner avec la règle du parallélogramme, dans le lien suivant, vous pouvez consulter plus d’exemples et plusieurs exercices résolus d’addition de vecteurs . Sur cette page, vous trouverez également d’autres méthodes pour ajouter des vecteurs graphiquement et même comment les ajouter numériquement.
Règle de parallélogramme pour soustraire deux vecteurs
La règle ou la méthode du parallélogramme est également utilisée pour soustraire deux vecteurs d’un graphique. Ainsi, les étapes à soustraire vectoriellement sont :
- Premièrement, nous représentons les deux vecteurs sur le graphique et les positionnons au même point d’application, c’est-à-dire que nous plaçons les origines des deux vecteurs au même point.
- Deuxièmement, nous dessinons le vecteur opposé du vecteur qui est soustrait dans l’opération, ou en d’autres termes, nous inversons le vecteur qui se soustrait.
- Ensuite, nous traçons une ligne parallèle au vecteur de changement de signe à la fin du vecteur qui s’additionne à . Et nous répétons le processus avec l’autre vecteur. De sorte que nous obtiendrons le dessin d’un parallélogramme (d’où le nom de la règle).
- Enfin, le résultat de la soustraction sera le vecteur qui va de l’origine commune des deux vecteurs au point où les deux droites parallèles se croisent.
Regardez l’exemple générique suivant dans lequel deux vecteurs sont soustraits par la loi du parallélogramme :
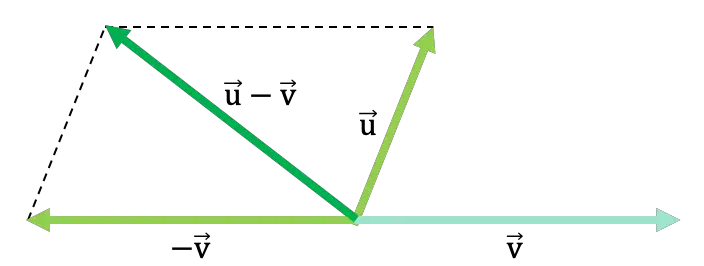
Dans le lien suivant, vous pouvez voir plus d’exemples de soustraction vectorielle avec la règle du parallélogramme, vous pouvez également vous entraîner avec des exercices de soustraction vectorielle résolus . De plus, vous trouverez d’autres techniques pour soustraire des vecteurs de leur graphique et, enfin, comment ils sont soustraits numériquement.
Enfin, si l’explication de cette technique vous a été utile, vous serez sûrement aussi intéressé de savoir quelle est la règle de la main droite . Sur la page de lien, vous pouvez voir en quoi il consiste, à quelle opération vectorielle il est utilisé et les différentes variantes de cette règle qui existent.