Position relative de deux droites dans le plan

Sur cette page vous trouverez l’explication des différentes méthodes qui existent pour déterminer la position relative de deux droites dans le plan (en R2). De plus, vous verrez plusieurs exemples et vous pourrez vous entraîner avec des exercices résolus étape par étape.

Quelle est la position relative de deux droites dans le plan ?

Avant de regarder les positions relatives entre deux droites dans le plan, évidemment il faut savoir exactement ce qu’est une droite, on peut la trouver dans la définition de droite .

Ainsi, lorsque l’on travaille à deux dimensions (en R2), il existe 3 types de positions relatives possibles entre deux droites :

D’autre part, l’angle entre deux droites dans le plan dépend aussi de leur position relative :

• Les lignes sécantes se croisent en formant un angle compris entre 0º (non inclus) et 90º (inclus). De plus, s’ils forment juste un angle droit de 90º, cela signifie que les deux lignes sont perpendiculaires.
• Les droites parallèles forment un angle de 0º, puisqu’elles ont la même direction.
• Et, pour la même raison, les lignes coïncidentes font également un angle de 0º entre elles.

Si vous voulez savoir comment l’angle entre deux lignes est calculé, vous pouvez consulter la formule de l’angle entre deux lignes . Vous trouverez ici une explication détaillée de la façon de déterminer l’angle entre deux lignes, ainsi que plusieurs exemples et même des exercices résolus pour pouvoir pratiquer et bien comprendre le concept.

Comment trouver la position relative de deux droites dans le plan

La connaissance de la position relative entre deux lignes dans un espace à deux dimensions dépend de la manière dont les lignes sont exprimées :

• Vecteurs directeurs des lignes : si deux lignes ont un vecteur directeur différent, elles doivent obligatoirement se couper. Par contre, si les coordonnées de leurs vecteurs directeurs sont égales ou proportionnelles, ils peuvent être parallèles ou coïncider (il faut vérifier s’ils ont un point commun).

• Équation explicite : lorsque deux droites ont des pentes différentes 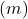ils sèchent Au contraire, si les droites ont la même pente mais un ordre différent à l’origine 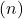ils sont parallèles. Enfin, deux droites sont confondues lorsqu’elles ont à l’origine des pentes et des ordonnées égales.

• Équation générale (ou implicite) : deux droites à coefficients non proportionnels A et B seront toujours sécantes. Cependant, ils seront parallèles lorsque ces deux paramètres sont proportionnels entre eux mais pas au coefficient C. Et, enfin, lorsque les trois termes sont proportionnels, cela implique que les droites sont confondues.

Si vous avez des doutes sur les équations de la droite ci-dessus, vous pouvez consulter l’explication des équations de la droite dans le plan . Vous trouverez ici la formule de toutes les équations de la ligne, comment elles sont calculées, des exemples et des exercices résolus des équations de la ligne.

Dans le tableau suivant, vous avez un résumé des propriétés précédentes :

Ensuite, nous allons voir deux exemples de la façon de déterminer la position relative entre deux lignes :

Exemple 1

• Trouver la position relative entre les deux lignes suivantes définies sous la forme d’une équation explicite :

Les deux droites ont la même pente :

Mais ils ont des ordonnées différentes à l’origine :

Donc, comme elles ont la même pente mais des ordonnées différentes à l’origine, les droites sont parallèles .

Exemple 2

• Déterminer la position relative entre les deux droites suivantes exprimées avec leur équation implicite (ou générale) :

Les deux lignes sont exprimées sous la forme d’une équation explicite, par conséquent, nous devons voir si l’un de leurs coefficients est proportionnel :

Les 3 termes des droites sont proportionnels, donc les droites coïncident .

Déterminer la position relative de deux droites dans le plan avec un système d’équations

Une autre façon de connaître la position relative entre deux lignes est d’analyser le système d’équations formé par les équations des lignes :

• Si le système a une solution unique , les droites se coupent. De plus, le point d’intersection des deux droites est la solution du système.
• S’il s’agit d’un système sans solution , cela indique que les droites n’ont aucun point commun et, par conséquent, ce sont des droites parallèles.
• Si le système a une infinité de solutions , cela signifie que les lignes ont tous les points en commun et, par conséquent, ce sont des lignes qui se coupent.

Exemple 3

• Calculez la position relative des deux droites suivantes à l’aide d’un système d’équations :

Pour trouver la position relative des deux lignes, nous devons résoudre le système d’équations linéaires suivant formé par les deux lignes :

Dans ce cas, nous allons résoudre le système avec la méthode de substitution. Nous allons donc isoler la variable

de la deuxième équation et substituez-la dans la première équation :

Et une fois qu’on sait combien vaut l’inconnu

On substitue sa valeur dans l’expression trouvée de

Nous n’avons donc obtenu qu’une seule solution du système d’équations composé des deux droites, donc les deux droites se coupent . Et le point où ils se croisent est la solution du système, c’est-à-dire le point

Problèmes résolus de position relative de deux lignes dans le plan

Exercice 1

Déterminez si les lignes suivantes se croisent, sont parallèles ou coïncident :

Les deux lignes sont exprimées sous la forme d’une équation implicite (ou générale), par conséquent, nous devons voir si l’un de leurs coefficients est proportionnel :

Seuls les coefficients A et B des droites sont proportionnels entre eux, et non au coefficient C. Donc les deux droites sont parallèles .

Exercice 2

Trouvez la position relative entre les deux droites suivantes exprimées sous forme d’équations paramétriques :

Nous pourrions résoudre le système d’équations formé par les deux lignes pour trouver leur position relative. Cependant, comme ils sont sous la forme d’équations paramétriques, on peut facilement trouver leurs vecteurs directeurs et s’ils ne sont pas proportionnels, cela signifie que les lignes se coupent. Et dans ce cas, nous ne passerons pas autant de temps à résoudre tout un système d’équations.

Pour que les coordonnées cartésiennes du vecteur directeur de chaque ligne soient les nombres devant le paramètre

Une fois que nous connaissons les vecteurs directeurs, nous vérifions leur proportionnalité :

Les vecteurs directeurs ne sont pas proportionnels, par conséquent, les lignes se croisent .

Exercice 3

Indiquez si les lignes suivantes se croisent, sont parallèles ou coïncidents et trouvez également un point d’intersection entre elles (le cas échéant).

Les deux droites sont définies par leur équation explicite et ont des pentes différentes :

Comme elles ont des pentes différentes, les droites se croisent .

Par conséquent, puisque les lignes se croisent, elles auront 1 point en commun et pour le calculer, nous devons résoudre le système d’équations formé par les deux lignes :

Dans ce cas, nous allons résoudre le système avec la méthode d’égalisation car les deux

sont déjà effacés :

Et une fois que nous avons l’inconnu

nous substituons sa valeur dans toute expression de pour savoir combien ça vaut :

Donc le point d’intersection des deux droites est le résultat du système :

Exercice 4

Calculer la valeur des inconnues

et de sorte que les deux droites suivantes soient parallèles :

Les lignes sont décrites sous forme d’équation générale (ou implicite). Par conséquent, pour que les deux droites soient parallèles, leurs coefficients A et B doivent être proportionnels, c’est-à-dire que l’équation suivante doit être remplie :

Il faut donc résoudre l’équation précédente pour obtenir la valeur de l’inconnue

Pour ce faire, on multiplie les fractions en croix :

Par contre, pour que les droites soient parallèles leurs termes indépendants ne peuvent pas être proportionnels aux autres coefficients :

Par conséquent, comme précédemment, nous résolvons l’inégalité en multipliant les fractions en croix :

Bref, pour que les deux droites soient parallèles

doit être 2 et peut être n’importe quel nombre réel sauf 3.

Exercice 5

Trouver l’équation explicite de la droite parallèle à la droite

et ce qui se passe à travers le point être hétéro

Pour que la droite soit parallèle à la droite

les deux doivent avoir la même pente. et la pente de la droite est 2 :

Par conséquent, l’équation de la droite que nous devons trouver sera la suivante :

Et une fois que l’on connaît la pente de la droite, on peut calculer l’ordonnée à l’origine en substituant le point qui appartient à la droite dans l’équation de la droite :

Donc l’équation explicite de la droite est :

Si vous êtes arrivé jusqu’ici, cela signifie que vous avez déjà maîtrisé les positions relatives entre deux lignes dans le plan. Bon travail!

Mais une chose que beaucoup se demandent est… et à quoi sert de connaître la position relative entre deux lignes ?

Eh bien, une des applications de la position relative entre lignes est de pouvoir connaître la distance entre 2 lignes, puisque le calcul de la distance entre deux lignes dépend de leur position relative :

• Si les lignes se croisent ou coïncident, la distance est nulle.
• En revanche, lorsque les droites sont parallèles, une formule spécifique doit être appliquée. Si vous êtes plus intéressé, vous pouvez consulter comment la distance entre deux lignes parallèles est calculée.