Sur cette page vous trouverez tout sur les lignes sécantes : ce qu’elles signifient, les différents types qui existent, comment savoir si deux lignes sont sécantes, comment trouver leur point commun,… Vous pourrez également voir plusieurs exemples et exercices résolus de lignes sécantes.
Quelles sont deux lignes qui se croisent ?
En mathématiques, la définition des droites sécantes est la suivante :
Deux droites se coupent lorsqu’elles ne se coupent qu’en un seul point. Par conséquent, les lignes qui se croisent n’ont qu’un seul point en commun. De plus, deux droites sécantes doivent nécessairement être contenues dans le même plan cartésien.
Le concept selon lequel deux lignes qui se croisent en un seul point est important, car si elles avaient plus d’un point d’intersection, elles seraient des lignes coïncidentes et, d’autre part, si elles n’avaient aucun point d’intersection, elles seraient des lignes parallèles.
Exemples de lignes sécantes
Une fois que nous avons vu la signification de deux lignes qui se croisent, voyons maintenant 2 exemples différents de ce type de lignes :
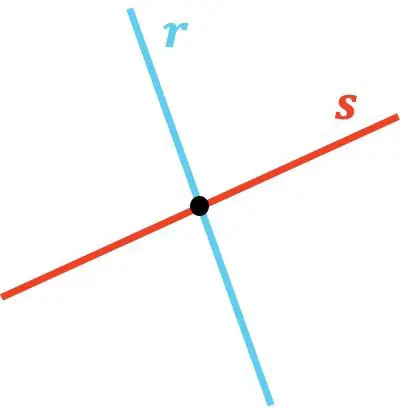
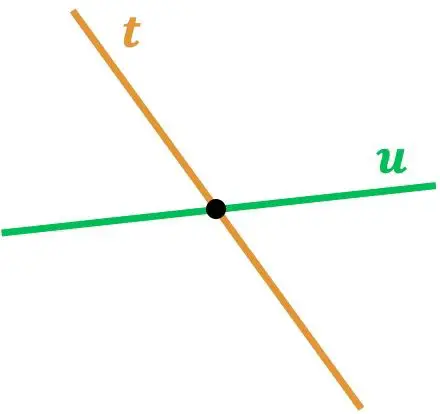
Comme vous pouvez le voir, les lignes r et s se coupent car elles se touchent en un point. Et, de la même manière, la ligne t coupe la ligne u puisqu’il y a un point où elles se coupent.
Types de lignes sécantes
Il existe deux types de lignes sécantes :
- Lignes perpendiculaires : sont des lignes qui se coupent en formant un angle droit de 90º.
- Lignes obliques : consistent en des lignes qui se croisent en formant un angle aigu entre 0º et 90º (non inclus).
Lignes droites perpendiculaires

Les lignes perpendiculaires sont ces lignes qui se croisent en formant quatre angles de 90 degrés.
De même, les pentes de deux droites perpendiculaires vérifient toujours la condition suivante :
![]()
Une autre des propriétés des lignes sécantes perpendiculaires est que le produit scalaire entre leurs vecteurs de direction (un vecteur qui indique la direction d’une ligne) est égal à zéro.
![]()
Si vous êtes plus intéressé par les lignes perpendiculaires, dans ce lien vous pouvez voir des exemples de lignes perpendiculaires . De plus, vous trouverez également comment calculer une droite perpendiculaire à une autre, les propriétés de ce type de droite, des exercices résolus pas à pas, etc.
lignes obliques

Les lignes obliques sont ces lignes qui se croisent en formant des angles aigus et des angles obtus deux à deux. C’est-à-dire faire deux angles aigus (inférieurs à 90º) et deux angles obtus (supérieurs à 90º). Or, selon la définition de l’angle de deux droites, l’angle entre deux droites est le plus petit de ceux qu’il forme.
L’angle entre deux lignes obliques avec leurs pentes peut être calculé à l’aide de la formule suivante :
![]()
Comment savoir si deux droites se coupent ?
Il existe principalement 3 méthodes pour trouver la position relative de deux droites :
- Avec les vecteurs directeurs des deux droites.
- Avec les pentes des deux lignes.
- Avec l’équation implicite (ou générale) des deux droites.
Ensuite nous allons voir l’explication des 3 méthodes qui existent pour savoir quand deux droites se croisent.
A partir des vecteurs directeurs des lignes
Si les coordonnées des vecteurs directeurs (vecteur qui marque la direction d’une droite) de deux droites différentes ne sont pas proportionnelles , ces deux droites se coupent.
Voyons un exercice résolu pas à pas de deux droites sécantes :
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8a2fa136f2840fc1f680e0f7f10ed6_l3.png)
Les deux lignes sont exprimées sous la forme d’équations paramétriques, de sorte que les composantes du vecteur directeur de chaque ligne sont les nombres devant le paramètre
![]()
![]()
Donc, pour voir si les vecteurs directeurs sont proportionnels, nous devons diviser leurs coordonnées entre elles. Si nous obtenons le même résultat dans les deux divisions, elles seront proportionnelles ; par contre, si le résultat est différent, cela signifiera que les vecteurs ne sont pas proportionnels.
![]()
Les divisions des composants ne sont pas équivalentes, par conséquent, les vecteurs ne sont pas proportionnels et, par conséquent, les lignes se croisent.
au départ des pistes
Si deux droites ont des pentes différentes , cela implique que les droites se coupent.
Par exemple, les deux droites suivantes se croisent car elles ont des pentes différentes :
![]()
La pente de la ligne
![]() est -2 et la pente de la droite
est -2 et la pente de la droite![]() est 3.
est 3.
![]()
Comme les deux droites n’ont pas la même pente, elles se coupent.
De l’équation implicite de la droite
Il peut également être trouvé si deux lignes se coupent ou non grâce aux équations implicites (ou équations générales) des lignes. L’équation implicite de la droite est la suivante :
![]()
Ainsi, deux droites sont sécantes lorsque leurs coefficients A et B ne sont pas proportionnels.
Voyons un exemple de deux droites sécantes définies avec leur équation implicite :
![]()
Pour vérifier qu’il s’agit de deux droites sécantes, il faut analyser la proportionnalité du coefficient A (nombre devant la variable
![]() ) avec le coefficient B (chiffre devant la variable
) avec le coefficient B (chiffre devant la variable![]() ):
):
![]()
Les deux termes ne sont pas proportionnels, donc effectivement les deux lignes se croisent.
Trouver le point commun de deux droites qui se croisent
Comme nous l’avons vu, les lignes qui se coupent n’ont qu’un seul point en commun. Ainsi, pour calculer le point d’intersection de deux droites sécantes , il faut résoudre le système d’équations formé par les deux droites.
A titre d’exemple, nous allons trouver le point d’intersection des deux droites suivantes :
![]()
Pour déterminer le point d’intersection des deux droites, il faut résoudre le système d’équations linéaires formé par les deux droites :
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77ae257986963d3652d5996fc09be9fb_l3.png)
Dans ce cas, nous allons résoudre le système avec la méthode de substitution. Nous allons donc isoler la variable
![]() de la première équation et substituez-la dans la deuxième équation :
de la première équation et substituez-la dans la deuxième équation :
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3ad955c3f2ebeb8ad0bdee85a226c73b_l3.png)
![]()
![]()
![]()
![]()
![]()
Et une fois qu’on sait combien vaut l’inconnu
![]() On substitue sa valeur dans l’expression trouvée pour
On substitue sa valeur dans l’expression trouvée pour ![]()
![]()
![]()
La solution du système d’équations est donc le point d’intersection des deux droites. Et ce point est
![]()
ligne sécante à un cercle
Normalement, lorsque nous disons que deux lignes se coupent, nous nous référons au concept que nous venons de voir. Cependant, en géométrie, il y a une autre signification de la ligne sécante :
Une ligne sécante avec un cercle est une ligne qui coupe un cercle (ou une courbe) en deux points différents.
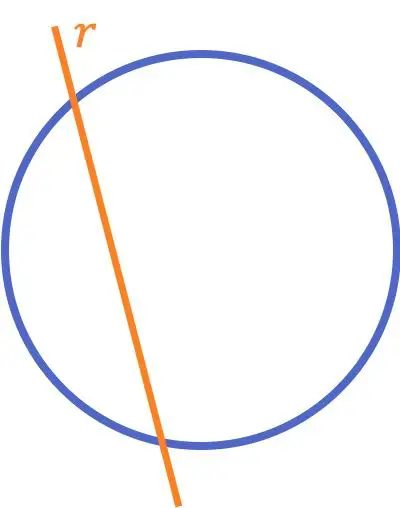
Contrairement au concept de deux lignes qui se croisent habituellement enseigné à l’école primaire, cette définition d’une ligne sécante avec un cercle est souvent étudiée dans les cours ultérieurs avec toutes les positions relatives des lignes avec les cercles.