Lignes perpendiculaires (perpendicularité) -

Sur cette page vous trouverez tout sur les droites perpendiculaires : ce qu’elles sont, quand deux droites sont perpendiculaires, comment calculer une droite perpendiculaire à une autre, ses propriétés,… De plus, vous pourrez voir des exemples et vous pourrez vous entraîner avec des exercices résolus pas à pas.

Que sont deux droites perpendiculaires ?

En mathématiques, deux droites sont perpendiculaires lorsqu’elles se coupent en un point formant quatre angles droits égaux (90º).

De plus, les vecteurs directeurs de deux droites perpendiculaires doivent également être perpendiculaires.

La perpendicularité de deux lignes est généralement indiquée par le symbole

$\perp .$

D’autre part, rappelez-vous que dans le plan il y a 4 possibilités dans le concept de position relative entre deux lignes : deux lignes peuvent être sécantes, perpendiculaires, coïncidentes ou parallèles. Si vous le souhaitez, vous pouvez vérifier la signification de chaque type de ligne sur notre site Web.

Comment savoir si deux droites sont perpendiculaires ?

Il existe deux façons de déterminer quand deux droites sont perpendiculaires, à partir de leurs vecteurs directeurs ou par leurs pentes . Vous avez ci-dessous l’explication des deux méthodes, bien qu’elles servent le même objectif, nous vous recommandons de savoir comment faire les 2 procédures car chacune dépend de la manière dont les lignes sont exprimées.

A partir des vecteurs directeurs des lignes

Une façon de savoir quand deux droites sont perpendiculaires est d’utiliser les vecteurs directeurs des droites en question. Rappelez-vous que le vecteur de direction est ce vecteur qui indique la direction d’une ligne.

Les vecteurs directeurs de deux droites perpendiculaires sont également orthogonaux entre eux. Par conséquent, si le produit scalaire des vecteurs directeurs de deux lignes est égal à 0, cela signifie que les lignes sont perpendiculaires.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Voyons comment la perpendicularité de deux droites est déterminée à partir d’un exemple :

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Les deux lignes sont exprimées sous la forme d’équations paramétriques, de sorte que les composantes du vecteur directeur de chaque ligne sont les nombres devant le paramètre

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Une fois que l’on connaît le vecteur directeur de chaque droite, on vérifie si elles sont perpendiculaires en calculant le produit entre les vecteurs :

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

Le produit scalaire des deux vecteurs est égal à zéro, donc les lignes sont perpendiculaires.

Des pentes des lignes

Une autre façon de déterminer si deux droites sont perpendiculaires consiste à utiliser leurs pentes. Rappelez-vous que la pente d’une droite est le coefficient

$m$ de l’équation explicite et de l’équation point-pente d’une droite.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Et la pente d’une droite peut également être obtenue à partir des coefficients

$A$ et $B$ de l’équation implicite (ou générale) d’une droite :

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Ainsi, les pentes de deux droites perpendiculaires sont inverses et de signe opposé, c’est-à-dire que l’égalité suivante est toujours satisfaite :

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Donc si le produit des pentes de deux droites différentes est égal à -1, cela implique que les droites sont perpendiculaires :

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Par exemple, les deux droites suivantes sont perpendiculaires :

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

On peut montrer qu’il s’agit de deux droites perpendiculaires l’une à l’autre à partir de leurs pentes. La pente de chaque droite vaut :

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Maintenant, nous multiplions les pentes :

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

Le produit entre les deux pentes est équivalent à -1, ce qui signifie en fait deux lignes perpendiculaires l’une à l’autre.

Comment calculer une droite perpendiculaire à une autre ?

Bien que cela puisse sembler difficile à faire, trouver une droite perpendiculaire à une autre est assez simple, pour cela vous n’avez besoin que d’un vecteur de direction perpendiculaire à la droite et d’un point qui appartient à la droite.

La seule difficulté est que, comme précédemment, la procédure dépend du type d’équation dans laquelle les lignes sont exprimées. Parce qu’une droite perpendiculaire à une autre peut être calculée à partir des vecteurs directeurs ou à partir des pentes .

A partir du vecteur directeur de la droite

Une droite perpendiculaire à une autre droite donnée peut être trouvée en utilisant son vecteur directeur. Voyons comment cela se fait avec un exemple :

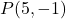Calculer la droite perpendiculaire à la droite $r$ ce qui passe par le point $P(5,-1)$ . être hétéro $r:$

$\displaystyle r : \ 3x+2y-1=0$

La première chose que nous devons faire est d’identifier le vecteur directeur de la ligne. Dans ce cas, la ligne est définie sous la forme d’une équation générale (ou implicite), par conséquent, les coordonnées cartésiennes du vecteur directeur de la ligne peuvent être obtenues avec les coefficients A et B de la ligne :

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

Et une fois que l’on connaît le vecteur directeur de la droite, il faut calculer un vecteur perpendiculaire à celle-ci. Pour cela, il suffit d’ insérer les coordonnées du vecteur et de changer le signe de l’un d’entre eux (celui que vous voulez) :

$\vv{\text{v}}_\perp =(3,2)$

Alors maintenant, nous connaissons le vecteur de direction de la ligne. L’équation implicite de la droite sera donc la suivante :

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Par conséquent, il suffit de déterminer le paramètre C. Pour ce faire, nous substituons le point qui appartient à la droite dans son équation et résolvons l’équation résultante :

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

En conclusion, l’équation de la droite perpendiculaire est :

$\bm{2x-3y-13=0}$

De la pente de la ligne

Une autre façon de trouver une ligne perpendiculaire à une certaine ligne est à partir de sa pente. Voyons comment ce type de problème est résolu à travers un exemple :

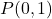Calculer la droite perpendiculaire à la droite $r$ ce qui passe par le point $P(0,1)$ . être hétéro $r:$

$\displaystyle r : \ y=4x-3$

La pente de la ligne

$r$ est:

$m_r = 4$

Une fois que nous connaissons la pente de la droite, nous devons trouver la pente de la droite perpendiculaire. Comme nous l’avons vu dans les sections ci-dessus, les pentes de deux droites perpendiculaires sont inverses et ont leur signe changé. Par conséquent, pour déterminer la pente de la ligne perpendiculaire, nous devons inverser la pente trouvée et changer son signe :

$m_\perp =-\cfrac{1}{4}$

L’équation explicite de la droite perpendiculaire sera donc la suivante :

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Enfin, on calcule l’ordonnée à l’origine de la droite perpendiculaire en substituant les coordonnées du point dans l’équation de la droite :

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

En bref, l’équation de la droite perpendiculaire est :

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Propriétés des droites perpendiculaires

Toutes les lignes perpendiculaires ont les caractéristiques suivantes :

Relation symétrique : Si une ligne est perpendiculaire à une autre ligne, cette ligne est également perpendiculaire à la première ligne.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Propriété non réflexive : Évidemment, aucune droite ne peut être perpendiculaire à elle-même.

$r \ \cancel{\bm{\perp}}} \ r$

Théorème : En géométrie euclidienne (en R2), toute paire de droites perpendiculaires à une troisième droite doit nécessairement être parallèle. Autrement dit, si une ligne est perpendiculaire à une autre ligne et que cette ligne est également perpendiculaire à une troisième ligne, les première et dernière lignes sont parallèles.

Problèmes résolus de droites perpendiculaires

Exercice 1

Parmi les droites suivantes, lesquelles sont perpendiculaires à la droite

$r: y=3x+4$ ?

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

voir solution

La pente de la ligne

$r$ est 3 :

$m_r=3$

Et les pentes de deux droites perpendiculaires sont inverses et de signe opposé, donc la pente de toute droite perpendiculaire à la droite

$r$ doit être:

$m_\perp=-\cfrac{1}{3}$

De sorte que les droites perpendiculaires à la droite

$r$ sont ceux dont la pente est égale à $-\cfrac{1}{3}$ . C’est-à-dire que les lignes $\bm{b}$ et $\bm{e}.$

Exercice 2

Déterminez si les deux droites suivantes sont perpendiculaires :

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

voir solution

le droit

$r$ s’exprime sous la forme d’une équation paramétrique, telle que les composantes du vecteur directeur de ladite droite soient les nombres devant le paramètre $t:$

$\vv{\text{v}}_r =(-1,-3)$

D’autre part, la ligne droite

$s$ est défini sous la forme d’une équation continue, donc les coordonnées de son vecteur directeur sont les nombres des dénominateurs :

$\vv{\text{v}}_s =(4,6)$

Une fois que l’on connaît le vecteur directeur de chaque droite, on peut vérifier si elles sont perpendiculaires en calculant le produit des deux vecteurs :

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

Le produit scalaire des deux vecteurs est différent de zéro, donc les droites ne sont pas perpendiculaires .

Exercice 3

Trouver la droite perpendiculaire à la droite

$r$ ce qui passe par le point $P(-2,1)$ . être hétéro $r:$

$\displaystyle r : \ 4x-y+5=0$

voir solution

La première chose que nous devons faire est d’identifier le vecteur directeur de la ligne. Dans ce cas, la droite est définie sous la forme d’une équation générale (ou implicite), donc son vecteur directeur est :

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Une fois que nous connaissons le vecteur directeur de la droite, nous devons calculer un vecteur perpendiculaire à celle-ci. Pour cela, il suffit d’insérer les coordonnées du vecteur et de changer le signe de l’un d’entre eux (celui que vous voulez) :

$\vv{\text{v}}_\perp =(4,-1)$

L’équation implicite de la droite sera donc la suivante :

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

Il suffit donc de déterminer l’inconnue C. Pour ce faire, on substitue le point par lequel passe la droite dans son équation :

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Enfin, l’équation de la droite perpendiculaire est :

$\bm{-x-4y+2=0}$

Exercice 4

Trouver l’équation point-pente de la droite perpendiculaire à la droite

$r$ ce qui passe par le point $P(3,-2)$ . être hétéro $r:$

$\displaystyle r : \ y=5x+1$

voir solution

La pente de la ligne

$r$ est:

$m_r = 5$

Une fois que nous connaissons la pente de la droite, nous devons trouver la pente de la droite perpendiculaire. Pour cela, il suffit d’inverser la pente trouvée et de changer son signe :

$m_\perp =-\cfrac{1}{5}$

Enfin, il suffit de substituer la pente trouvée et les coordonnées du point dans l’équation point-pente de la droite :

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Exercice 5

le droit

$r$ passe par les points (2,1) et (4,2), et la droite $s$ passe par les points (-1,2) et (1,-2). Déterminez s’il s’agit de deux droites perpendiculaires ou non.

voir solution

Pour vérifier s’il s’agit de deux lignes perpendiculaires, nous calculerons leurs pentes, puis nous verrons si elles respectent la relation perpendiculaire. N’oubliez pas que la formule de la pente d’une droite est la suivante :

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

La pente de la ligne

$r$ est:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

La pente de la ligne

$s$ est:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

Pour vérifier la perpendicularité des deux droites, il faut voir si la pente d’une droite est l’inverse inverse de l’autre pente. Dans ce cas, les deux pentes sont inverses et ont également des signes opposés, donc les deux droites sont perpendiculaires l’une à l’autre.

Exercice 6

Calculer la valeur de

$k$ de sorte que les deux droites suivantes soient perpendiculaires :

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

voir solution

Les deux droites sont exprimées sous la forme d’une équation implicite (ou générale), et le vecteur directeur d’une équation implicite de la droite est :

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Par conséquent, le vecteur directeur de chaque ligne serait :

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

Pour que deux droites soient perpendiculaires, le produit scalaire de leurs vecteurs directeurs doit être nul. Par conséquent, nous appliquerons cette condition pour trouver la valeur de l’inconnue

$k:$